
高等数学在线开放课程 定积分及其应用 二、微元法: (1)根据问题的具体情况,选取积分变量,如x为积分变 量,并确定积分区间[a,b]: 1)选取变量x或y,∈[a,b] (2)设想把区间[a,b]分成n个小区间,取其中任一小区间并 记为[x,x+dx],求出相应于这小区间的部分分量△F的近似 值。如果△F能近似地表示为[a,b]上的一个连续函数在x处 的值f(x)与dx的乘积,就把f(x)dx乘积称为量F的微元且 记作dF,即dF=f(x)dx; 2)微元dF=f(x)dx
高 等 数 学 在 线 开 放 课 程 定积分及其应用 二、微元法: 1) 2)
高等数学在线开放课程 定积分及其应用 3)以所求量F的微元f(x)dx 为被积表达式,在区间[a,b]上 作定积分,得F=∫fx)dx 3) 写定积分F=f(x)dx 即为所求量F的积分表达式.这个方法通常叫做微元法. 应用方向: 平面图形的面积;体积;功;水压力等
高 等 数 学 在 线 开 放 课 程 定积分及其应用 这个方法通常叫做微元法. 应用方向: 平面图形的 面积;体积;功;水压力等. 3)
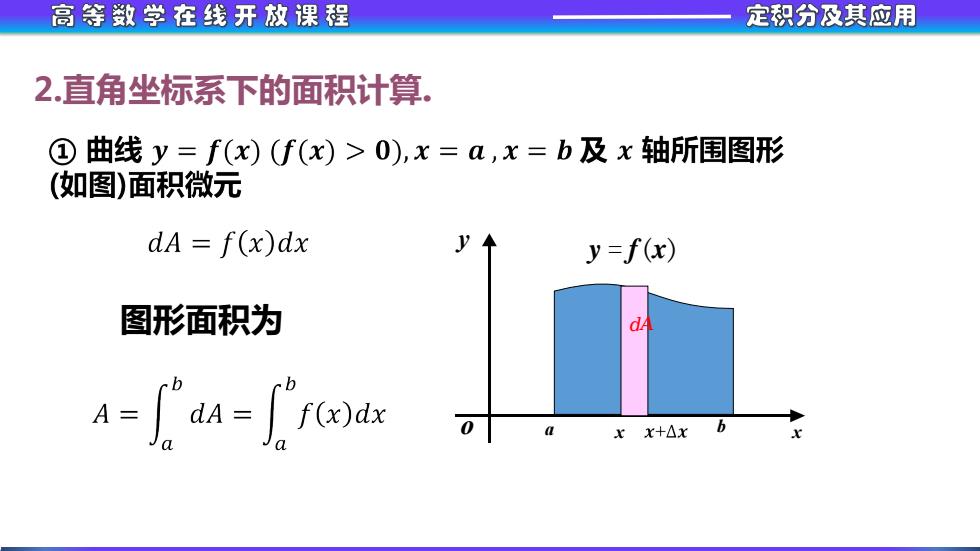
高等数学在线开放课程 定积分及其应用 2.直角坐标系下的面积计算. ①曲线y=f(x)f(x)>0),x=a,x=b及x轴所围图形 (如图)面积微元 dA f(x)dx y=f(x) 图形面积为 A=dA=f(x)dx xX+△x
高 等 数 学 在 线 开 放 课 程 定积分及其应用 2.直角坐标系下的面积计算. 图形面积为 x y o x ᵉ = ᵈ(ᵉ ) ᵅ ᵃ a b