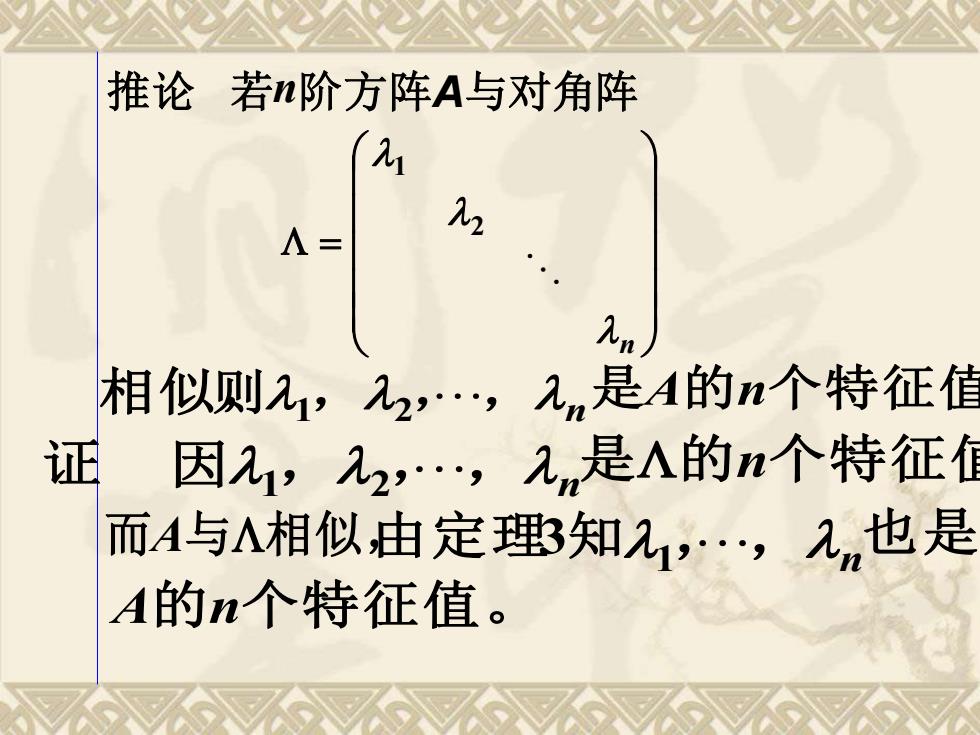
推论若n阶方阵A与对角阵 Λ= 22 An 相似则2,22,元n是A的n个特征值 证 因1,22,元n是的n个特征值 而A与A相似由定理知21,2也是 A的n个特征值
推论 若 n 阶方阵A与对角阵 = n 2 1 相似,则1 ,2 ,, n 是A的n个特征值。 证 因1 ,2 ,, n 是的n个特征值, 而A与相似,由定理3知1 ,, n A的n个特征值。 也是

利用对角矩阵计算矩阵多项式 若A=PBP1,则 k个 APBP-PBP1.PEP-PBPDPBP1. A的多项式 (A)=aA"+aA"++an-1A+arE =oPB"p-1+1PB"-1P-1+. an-iPBP+an PE P-I =P(ao B"+a B"++an-1B+an E)P Pe(B)P-1
利用对角矩阵计算矩阵多项式 , 1 A PB P − 若 = a PB P a PE P a P B P a P B P n n n n 1 1 1 1 1 1 1 0 − − − − − − + + = + + A = k A的多项式 A a A a A an A anE n n = + + + − + − 1 1 0 1 ( ) ( ) . 1 P B P− = . 1 P B Pk − = 则 P a B a B an B anE P n n 1 1 1 0 1 ( ) − − − = + ++ + PB P − 1 PBP−1 PBP−1 PBP−1 k个
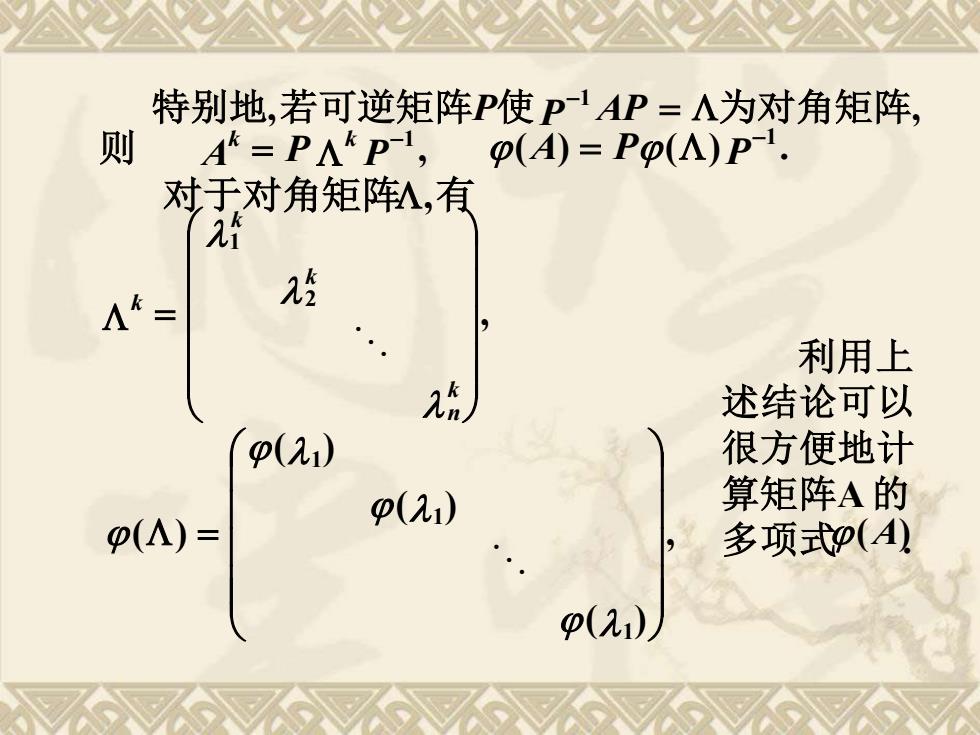
特别地,若可逆矩阵P使P1AP=A为对角矩阵, 则 Ak=PAP-,(A)=P(A)P. 对于对角矩阵私,有 2然 Λ= 5 利用上 述结论可以 p(21) 很方便地计 p() 算矩阵A的 p(A)= 多项式P(A) p(21)
, , 特别地 若可逆矩阵P使P −1 AP = 为对角矩阵 , 1 A P P k k − 则 = ( ) ( ) . 1 A P P − = 对于对角矩阵,有 , 2 1 = k n k k k , ( ) ( ) ( ) ( ) 1 1 1 = 利用上 述结论可以 很方便地计 算矩阵A 的 多项式 . (A)

定理 设f(2)是矩阵A的特征多项式则f(A)=O. 证明只证明A与对角矩阵相似的情形 若A与对角矩阵相似,则有可逆矩阵P,使 p-1AP=Λ=dig(21,.,m) 其中:为A的特征值f)=0.由A=PAP1,有 f(2) f(A)=Pf(A)P=P f(2m) =POP=O
定理 设f ()是矩阵A的特征多项式,则f (A) = O. 证明 只证明A与对角矩阵相似的情形. 若A与对角矩阵相似,则有可逆矩阵P,使 ( , , ), 1 1 P AP = = diag n − , ( ) = 0. i i 其中 为A的特征值 f 由A = P P −1 ,有 f (A) . 1 = PO P = O − Pf P 1 ( ) − = P f f P n 1 1 ( ) ( ) − =