
第8章多元函数积分学 8.1二重积分的概念与性质 8.2二重积分的计算 结束
8.1 二重积分的概念与性质 8.2 二重积分的计算 第8章 多元函数积分学 结束

8.1二重积分的概念与性质 8.1.1二重积分的概念 引例1曲顶柱体的体积. 若有一个柱体,它的底是Ox平面上的闭区域D, 它的侧面是以D的边界曲线为准 z=f(x,y) 线,且母线平行于轴的柱面, 它的顶是曲面z=孔xy), 设f孔x,)20为D上的连续函数. 我们称这个柱体为曲顶柱体 现在来求这个曲顶柱体的体积, 前页后页结求
前页 后页 结束 若有一个柱体,它的底是Oxy平面上的闭区域D, 它的侧面是以D 的边界曲线为准 线,且母线平行于z轴的柱面, 它的顶是曲面z=f(x,y), 设 f(x,y)≥0为D上的连续函数. 我们称这个柱体为曲顶柱体. 引例1 曲顶柱体的体积. z f x y = ( , ) 8.1.1 二重积分的概念 8.1 二重积分的概念与性质 现在来求这个曲顶柱体的体积. D
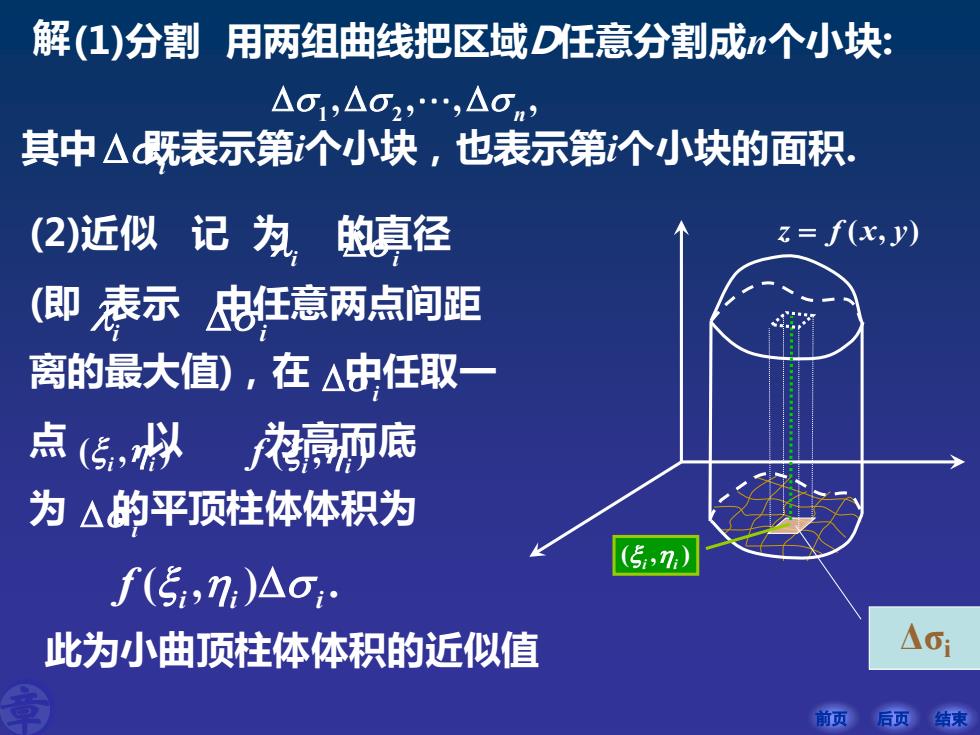
解(1)分割用两组曲线把区域D任意分割成个小块: △g1,△02,.,△on) 其中△既表示第个小块,也表示第个小块的面积, (2)近似记为【 的真径 f(x,y) (卿表示忠狂意两点间距 离的最大值),在△中任取一 点(传,以花丽底 为△的平顶柱体体积为 (5,7) f(5,7)△o 此为小曲顶柱体体积的近似值 △01 前页后页结束
前页 后页 结束 其中 既表示第i个小块,也表示第i个小块的面积. i (2)近似 记 为 的直径 (即 表示 中任意两点间距 离的最大值),在 中任取一 点 ,以 为高而底 为 的平顶柱体体积为 i i i i i ( , ) i i ( , ) i i f i ( , ) . i i i f 解(1)分割 用两组曲线把区域D任意分割成n个小块: 1 2 , , , , n z f x y = ( , ) ( , ) i i 此为小曲顶柱体体积的近似值 Δσi

(3)求和 把所有小平顶柱体的体积加起来,得到曲 顶柱体体积的近似值为 空f5n)Ao (4)取极限记入=max{2,入2,.,2n},若极限 i- 存在,则它即为所求曲顶柱体的体积: 前页后页结束
前页 后页 结束 (4) 取极限 记 = max{ , , , } 1 2 n ,若极限 0 1 lim ( , ) n i i i i f → = 存在,则它即为所求曲顶柱体的体积. (3) 求和 把所有小平顶柱体的体积加起来,得到曲 顶柱体体积的近似值为 1 ( , ) . n i i i i f =

1.二重积分的定义 定义设f(心y)是定义在闭区域D上的有界函数. 把区域D任意分割成n个小区域:△o,△o,△o。其 中△o表示第个小区域=1,2,n),也表示其面积.在每个小 区域△o;上任取一点(5,n),作和 ∑f5,n,)△c i=1 若为的直径,记元=max(2荐极限,} im∑f5,n,)△o 2>0 i=l 存在,则称为函数(在区域D上的定积分,记 ∬fx,y)do 即∬fx,y)ao=im∑f(5,n)△o 2→0 D i=1 前页后页结束
前页 后页 结束 1.二重积分的定义 定义 设f (x,y)是定义在闭区域D上的有界函数. 把区域 D 任意分割成n个小区域: 其 中 表示第i个小区域(i=1,2,.,n),也表示其面积.在每个小 区域 i 上任取一点 ,作和 i 1 2 , , , n , 1 ( , ) n i i i i f = 若 为 的直径,记 = max{ , , , } , 1 2 若极限 n 0 1 lim ( , ) n i i i i f → = i i ( , ) i i 存在,则称为函数 f x y ( , ) 在区域D上的定积分,记 ( , ) D f x y d 即 0 1 lim ( , ) n i i i i f → = ( , ) = D f x y d