
第1章函数极限与连续 1.1 函数 1.2极限的概念 1.3 极限的运算 1.4 函数的连续性 结束
1.1 函数 1.2 极限的概念 1.3 极限的运算 1.4 函数的连续性 第1章 函数极限与连续 结束

1.1函数 1.1.1 函数的概念 定义1设x与是两个变量,若当变量x在非空数集D内任取 一个数值时,变量x按照某种对应法则f总有一个确定的 数值y与之对应,则称变量为变量x的函数,记作 x∈Dy=f(x) 称D为该函数的定义域记为D,.称为自变量,称y为因变量, 当自变量x取数值x∈D时,与x,对应的因变量的值 称为函数y=f(x)在点,处的函数值,记为f(x,)或yk=,, 当x取遍D内的各个数值时,对应的变量,取值的全体组成 数集称做这个函数的值域记为Z,。 前页后页结束
前页 后页 结束 当自变量x取数值 时,与 对应的因变量y的值 称为函数 在点 处的函数值,记为 或 . 当x 取遍D内的各个数值时, 对应的变量y 取值的全体组成 0 x D 0 | x x y = 0 x 0 x 0 f x( ) 定义1 设x与y是两个变量,若当变量x在非空数集D内任取 一个数值时,变量x 按照某种对应法则f 总有一个确定的 数值y 与之对应,则称变量y为变量x 的函数,记作 称D为该函数的定义域.记为Df .称x为自变量,称y为因变量. x D 1.1.1 函数的概念 数集称做这个函数的值域.记为Zf 。 1.1 函 数 y f x = ( ) y f x = ( )

1.1.2 函数的表示法 (1)公式法用数学公式表示自变量和因变量之间的对应关 系,是函数的公式表示法如例1是用公式法表示函数, 刚1已知某商品的总成本函数为:G-Q@=10+亨 (2)表格法自变量x与因变量的一些对应值用表格列出 例2某工厂全年1一6月原材料进货数量如下表,这 里表达的是时间和原材料进货数量之间的关系. T(月) 2 4 5 6 Q(吨) 11 10 12 11 12 12 前页后页结来
前页 后页 结束 1.1.2 函数的表示法 例1 已知某商品的总成本函数为: 2 ( ) 100 4 Q C C Q = = + 例2 某工厂全年1—6月原材料进货数量如下表,这 里表达的是时间和原材料进货数量之间的关系. T(月) 1 2 3 4 5 6 Q(吨) 11 10 12 11 12 12 (1)公式法 用数学公式表示自变量和因变量之间的对应关 系,是函数的公式表示法.如例1是用公式法表示函数. (2)表格法 自变量x与因变量y的一些对应值用表格列出
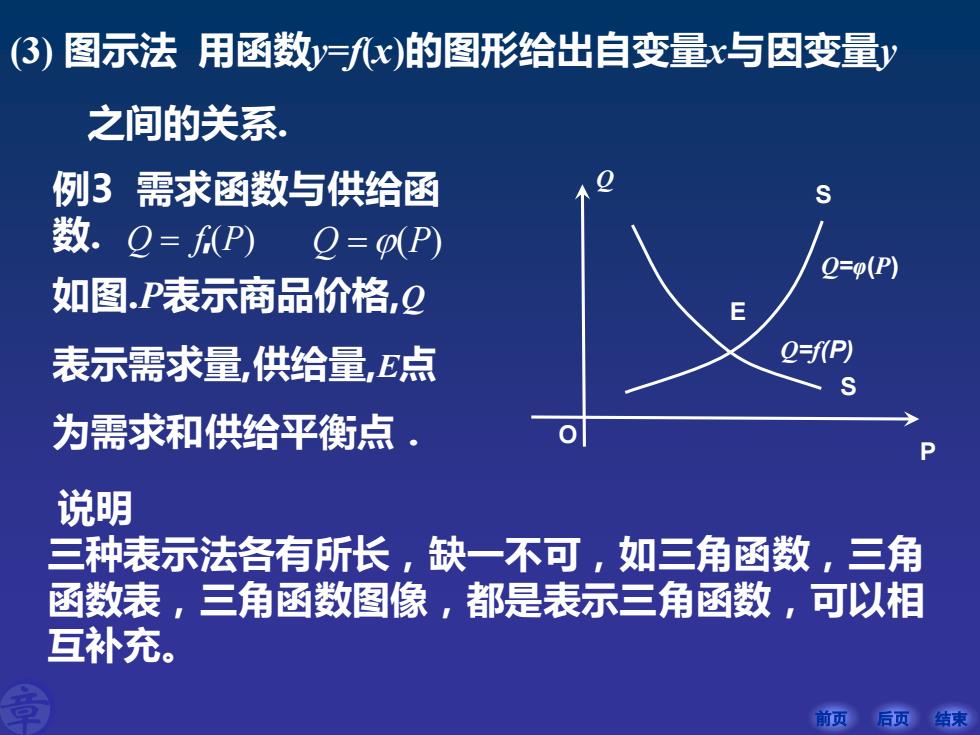
(3)图示法用函数yx)的图形给出自变量x与因变量y 之间的关系: 例3需求函数与供给函 数.Q=fP) Q=pP) O=0(P) 如图.P表示商品价格,Q 表示需求量,供给量,E点 Q=f(P) 为需求和供给平衡点· P 说明 三种表示法各有所长,缺一不可,如三角函数,三角 函数表,三角函数图像,都是表示三角函数,可以相 互补充。 前页后页结束
前页 后页 结束 (3) 图示法 用函数y=f(x)的图形给出自变量x与因变量y 之间的关系. 例3 需求函数与供给函 数. , 如图.P表示商品价格,Q 表示需求量,供给量,E点 为需求和供给平衡点. Q f P = ( ) Q P =( ) S S E Q P O Q=φ(P) Q=f(P) 说明 三种表示法各有所长,缺一不可,如三角函数,三角 函数表,三角函数图像,都是表示三角函数,可以相 互补充

注: (1)函数的定义域和对应法则是函数的两个主要要素 (2)如果两个函数具有相同的定义域和对应法则,则 它们是相同的函数 (3)在实际问题中,函数的定义域是由实际意义确定的 (4)在研究由公式表达的函数时,我们约定:函数的定义 域是使函数表达式有意义的自变量的一切实数值所组 成的数集, 例4求函数y= x+1 x+3 的定义域 解当分母 x+3≠0时,此函数式都有意义 因此函数的定义域为(-o,-3)U(-3,+∞) 前页后页结束
前页 后页 结束 例4 求函数 的定义域 (1)函数的定义域和对应法则是函数的两个主要要素。 注: (2)如果两个函数具有相同的定义域和对应法则,则 它们是相同的函数. (4)在研究由公式表达的函数时,我们约定:函数的定义 域是使函数表达式有意义的自变量的一切实数值所组 成的数集. (3)在实际问题中,函数的定义域是由实际意义确定的. 1 3 x y x + = + 解 当分母 x + 3 0 时,此函数式都有意义 因此函数的定义域为 ( , 3) ( 3, ) − − − +