
第5章定积分 5.1定积分的概念与性质 5.2微积分学基本定理 5.3定积分的积分法 5.4广义积分 结束
5.1 定积分的概念与性质 5.2 微积分学基本定理 5.3 定积分的积分法 5.4 广义积分 第5章 定积分 结束
5.1定积分的概念与性质 5.1.1引入定积分概念的实例 引例1曲边梯形的面积如图,由连续曲线yfx),直线 x=4,x=b及x轴围成的图形称为曲边梯形. 下面我们求曲边梯形的面积 y=f(x) (1)分割在(a,b)内插入n-1个分点 Q=X0<x<X2<<X-<X=b 把区间a,b]分成n个小区间 0 [x0,x1]x1x2][x,-1x,][xm-1,xn] 记每一个小区间xx的长度为△x,=x,-x=1,2) 前页后页结束
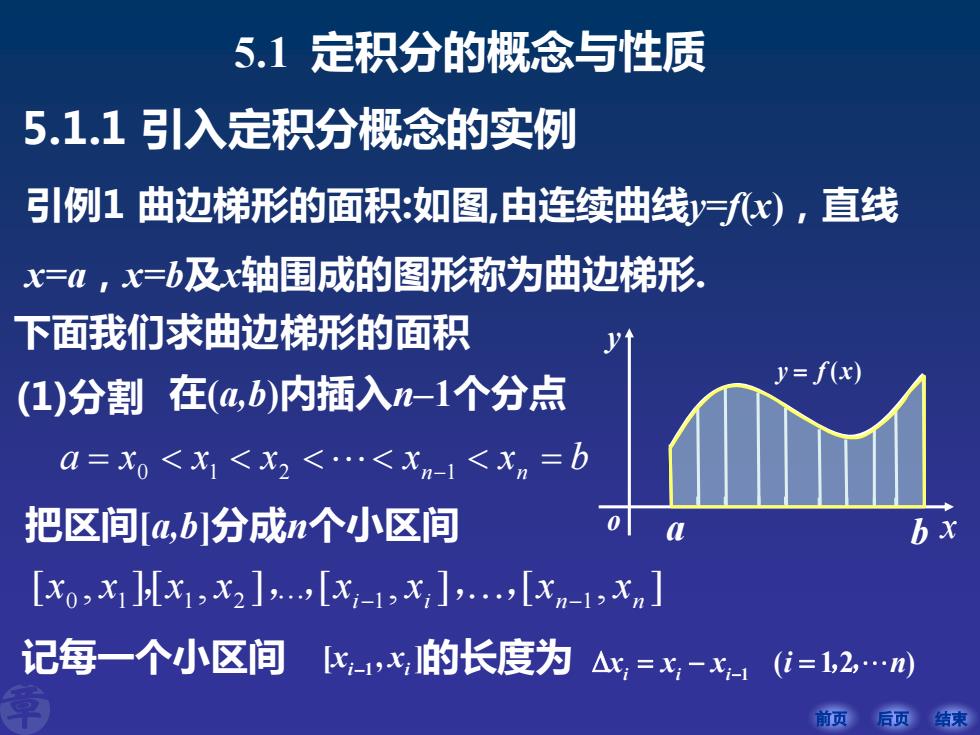
前页 后页 结束 5.1.1 引入定积分概念的实例 引例1 曲边梯形的面积:如图,由连续曲线y=f(x),直线 x=a,x=b及x轴围成的图形称为曲边梯形. 下面我们求曲边梯形的面积 (1)分割 在(a,b)内插入n–1个分点 a = x0 x1 x2 xn−1 xn = b [ , ][ , ] . [ , ] [ , ] 0 1 1 2 i 1 i n 1 n x x x x x x x x , , − ,, − 把区间[a,b]分成n个小区间 记每一个小区间 的长度为 1 ( 1 2 ) i i i [ , ] x x i i −1 = − = x x x i n − , a b x y f x = ( ) o y 5.1 定积分的概念与性质
过每个分点x,=1,2,)作轴的平行线,将曲边梯形 分割成n个小曲边梯形 (2)近似 △A表示第个小曲边梯形的面积,在小区间x-x,=1,2,m) 内任取一点化≤≤x),过点5,作x轴的垂线与曲线 交于点P(5,f(5》,以△x,为底,f(5)为高做矩形,以此 矩形做为小曲边梯形面积的近似值,则,A4≈△x,·f(传) (3)求和 y=f(x) 将所有矩形面积求和 An=f(5)△x1+f(5)△x2+.+f(5n)△x。 =Σf5,)△x 0 i=1 前页后页结束
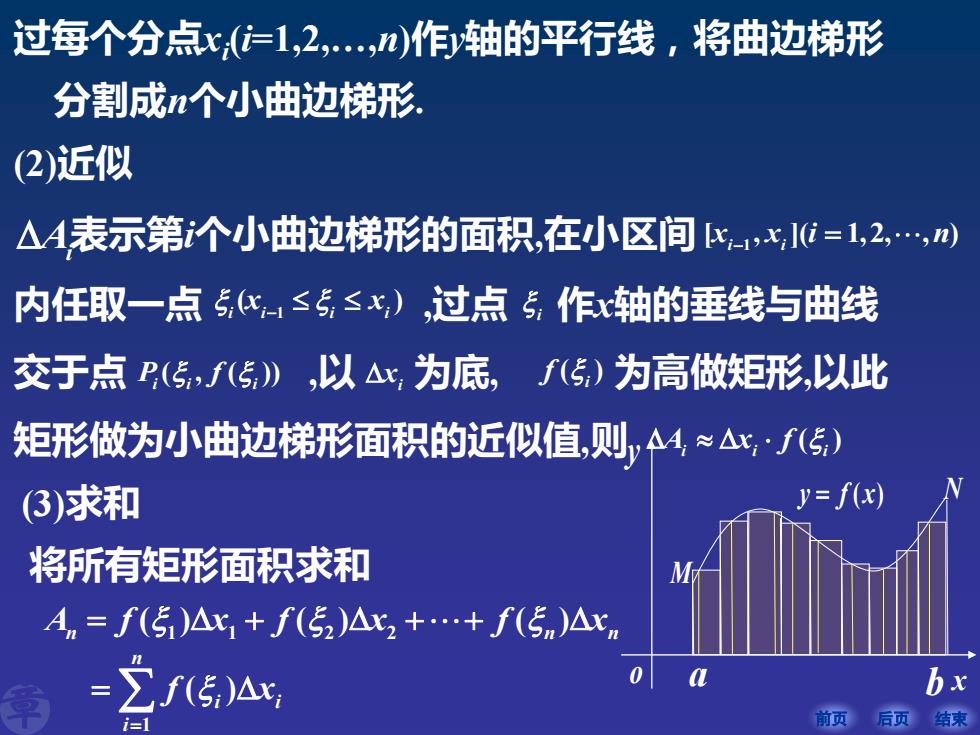
前页 后页 结束 (2)近似 表示第i个小曲边梯形的面积,在小区间 内任取一点 ,过点 作x轴的垂线与曲线 交于点 ,以 为底, 为高做矩形,以此 矩形做为小曲边梯形面积的近似值,则 Ai 1 [ , ]( 1,2, , ) i i x x i n − = 1 ( ) i i i i x x − i ( , ( )) P f i i i i x ( )i f ( ) A x f i i i a y f x = ( ) M N o y (3)求和 将所有矩形面积求和 1 1 2 2 ( ) ( ) ( ) A f x f x f x n n n = + + + 1 ( ) n i i i f x = = b x 过每个分点xi (i=1,2,.,n)作y轴的平行线,将曲边梯形 分割成n个小曲边梯形

则A,即是曲边梯形面积的近似值, (4)取极限 记入为所有小区间中长度的最大者,即2=max△x,}, 1≤i≤n 当入→0时,总和的极限就是曲边梯形面积A,即 A=im∑f(5△x →0 引例2变力做功 设某质点作直线运动,已知变力F()是位移s的 连续函数,质点的位区间为a,b],求变力F做的功 解(1)分割 在Ia,b]插入n个分点 4=S<S<S<.<S<<<=b 前页后页结束
前页 后页 结束 (4)取极限 记 为所有小区间中长度的最大者,即 , 当 时,总和的极限就是曲边梯形面积A,即 1 max{ }i i n x = → 0 0 1 lim ( ) n i i i A f x → = = 解 (1) 分割 引例2 变力做功 , . ( ) 连续函数,质点的位移区间为 ,求变力 做的功 设某质点作直线运动,已知变力 是位移 的 a b F F s s 在 插入n个分点 0 1 2 1 i n n a s s s s s s b = = − [ , ] a b 则 A n 即是曲边梯形面积的近似值

将闭区间4,b]分成个小区间: So,SS1,S2.,S-1S,.Sm-13Sn 小区间的长度 △s,=S-S-1(i=1,2,.,n) (2)近似 在每一个小区间s1,】上任取一点专,把F(传)做为 质点在小区间上受力的近似值,于是,力F在小区间s,1s,引 上对质点所做的功的近似值为 △W,≈F(5)△s(i=1,2,n) 前页 后页结束
前页 后页 结束 将闭区间[a,b]分成n个小区间: 0 1 1 2 1 1 [ , ],[ , ], ,[ , ], ,[ , ] i i n n s s s s s s s s − − 1 ( 1,2, , ) i i i = − = s s s i n − 小区间的长度 (2)近似 在每一个小区间 上任取一点 ,把 做为 质点在小区间上受力的近似值,于是,力F在小区间 上对质点所做的功的近似值为 1 [ , ] i i s s − i ( ) F i 1 [ , ] i i s s − ( ) ( 1,2, , ) W F s i n i i i =