《经济数学基础》课程PPT教学课件（线性代数）第二章 矩阵（3/4）

四.矩阵的分块， 1.分块矩阵的定义 2.分块矩阵的运算规则 1.分块矩阵的定义 对于行数和列数较高的矩阵A,为了 简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算.具体做法是：将 矩阵A用若干条纵线和横线分成许多个小 矩阵，每一个小矩阵称为A的子块，以子 块为元素的形式上的矩阵称为分块矩阵：

1 对于行数和列数较高的矩阵 ，为了 简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算. 具体做法是：将 矩阵 用若干条纵线和横线分成许多个小 矩阵，每一个小矩阵称为 的子块，以子 块为元素的形式上的矩阵称为分块矩阵. A A A 四. 矩阵的分块. 1. 分块矩阵的定义 2. 分块矩阵的运算规则 1. 分块矩阵的定义

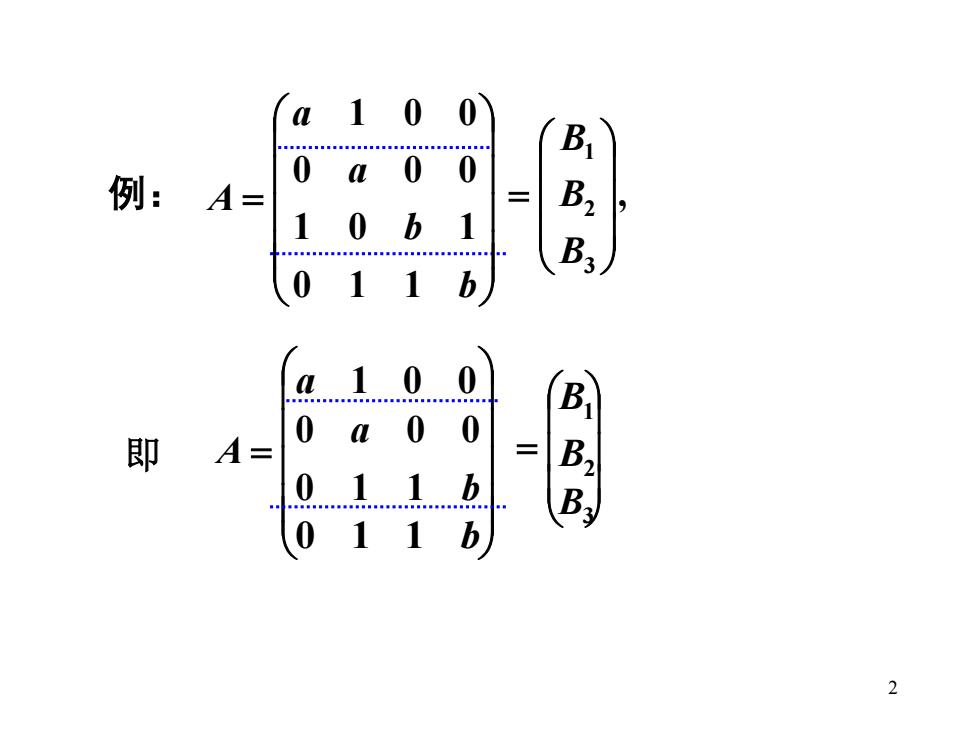
21 0 0 0 a 0 B 例：A= 1 0 1 B3 011 b a 1 0 0 0a0 0 即 A= 0.db BBB 011b 2

2 , 321   = BBB   = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 例：   A = a 1 0 0b a 0 1 1 0 0 0 0 1 1 b   = B 1 B 2 B 3 即

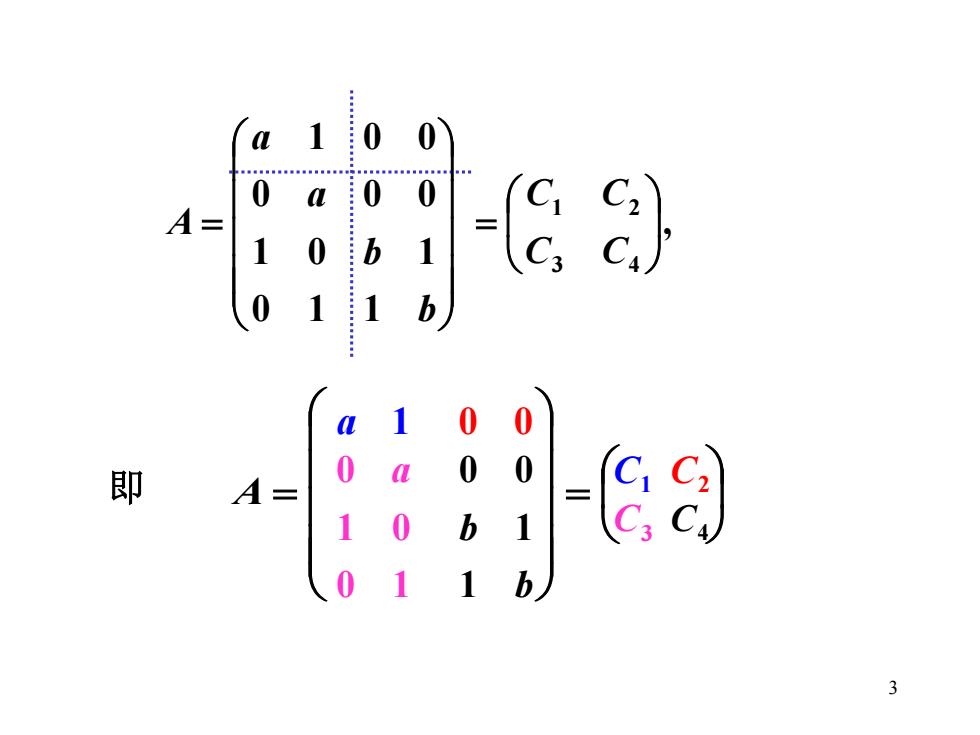
a 1 0 0 0 a 0 0 C A- 1 0 b 1 0 1 1 b 0 0 即 0 0 A= 1 0 b 01 0 1 h 3

3   = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 , 3 4 1 2   = C C C C   =  A = a 1 C 1 0 0 C 2 0 1 1 0 0 a C 3 b b1 1 0 0 C4 即

a 1 0 0 0 0 0 A 1 0 b 1 -任w-) 0 1 1 b se 1 0。 .0 0 A= 10000000110000110000010000010000 1 0b1 44专A烘w 0 : 4

4 ,      = E B A O ( ), = A1 A2 A3 A4               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0       = a a A 0 1 其中       = b b B 1 1       = 0 1 1 0 E       = 0 0 0 0 O               = 0 1 0 1 a 其中A               = 1 0 1 2 a A               = 1 0 0 3 b A               = b A 1 0 0 4

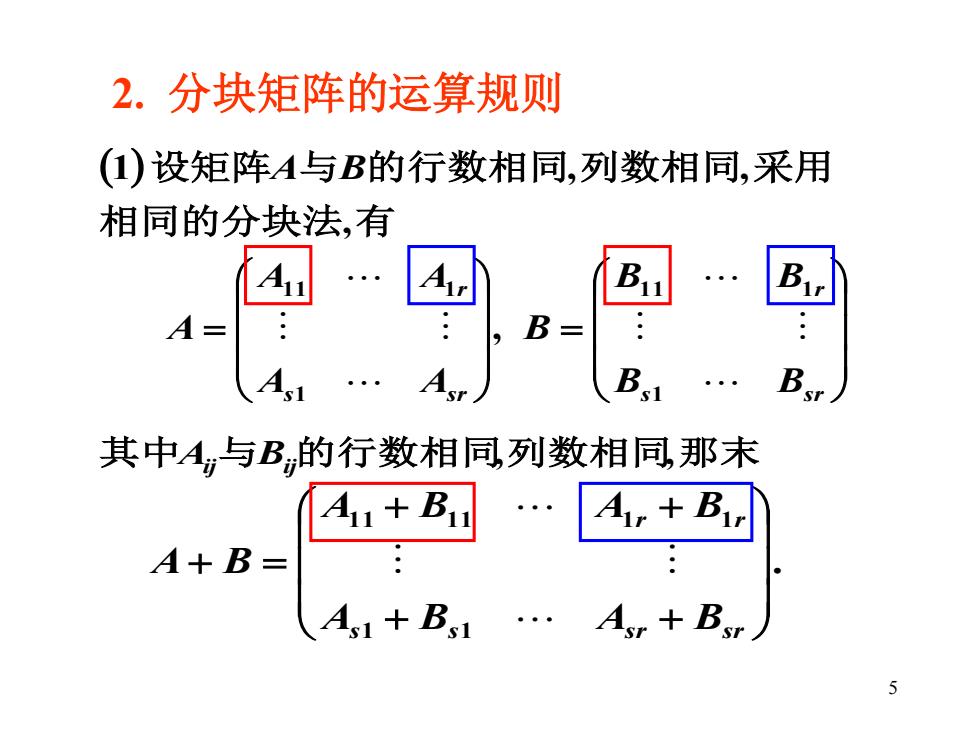
2.分块矩阵的运算规则 (1)设矩阵A与B的行数相同，列数相同，采用 相同的分块法，有 B A- 。B= A A B 其中A与B的行数相同列数相同，那未 A1+B. Air Bir A+B= 人A1+B1·An+Bn 5

5 ( ) 相同的分块法 有 设矩阵 与 的行数相同 列数相同 采用 , 1 A B , , 其中Aij与Bij的行数相同,列数相同,那末 . 1 1 1 1 1 1 1 1           + + + + + = s s sr sr r r A B A B A B A B A B               =           = s sr r s sr r B B B B B A A A A A         1 1 1 1 1 1 1 1 , 2. 分块矩阵的运算规则