
内 一、思想教育:历史上的今天 复习:复平面的点集 二、 新课内容: (-)复变函数 定义1:设E是复数:=x+以的集合,若存在一个法则,按此法则对于E的每一个:,都 有一个(或多个)确定的复数 +与之对应,那么就称为的复变函数。 记0 f(). 集合E称为函数0=f()的定义集合,与E中z对应的o值构成的集合E称为函数值集合,记为 f(E),即G=f(E). 若:的一个值对应着0的一个值,则称复变函数f()是单值的;若:的一个值对应着0的两个 或两个以上的值,则称复变函数f)是多值的。 与点z∈E对应的点0=fe)称为点:的像(Imago),同时点:就为点o=f(e)的原像(Inverse) 例1:0=2是定义在整个复平面上的函数: =二是定义在除原点外的整个复平面上的复变函数 o=E(e≠l,n≥2,n∈Z):0=g(e≠0)均为z的多值函数。 例2:0=二将:平面上的直线x=1映射成0平面上的何种曲线? 解:设:=x+y,0=1+iv= +,=1则@=1-少 x-iy 1+,s -V 2+2= 反函数:设函数0=f()定义在E上,值域为G若对于G中的任一点0,在E中存在一个或 几个点:与之对应,则在G上确定了一个单值或多值函数,记作:=(),称为0=f()的反 函数。若0=f()与它的反函数:=f-()都是单值的,那么称函数0=f()是一一对应的。 注:单值函数的反函数不 一定是单值函数。 (二)复变函数的极限与连续 1、复变函数的极限 定义2:设函数0=f(e)定义在:的去心邻域0<上-<r内。若存在常数A,对于任意给 定的6>0,都存在一正数6(0<6≤r),使得当0<上-<r时,有/e)-<6,则称函数 fe)当:→zo时的极限存在,常数A为其极限值,记作limf(:)=A。 定理1:设fe)=(x,y)+i(x,y),o=x+%,A=a+ib,则1imf(e)=A一 lim,)=a且imx,)=b. 定理2:极限四则运算法则(略) 例3:判断下列函数在原点处的极限是否存在,若存在,试求出其极限值。 ()/(=)-zRe(-) (2)/()-Re() 网 2、复变函数的连续 定义3:若1im∫(e)=f(o)则称fe)在:处连续。如果f(e)在区域D内每一点都连续,那 么函数f(e)在区域D内连续。 定理3:若f(巴),g(日)在点处连续,则其和、差、积、商(分母不为零)在。处连线
内 容 一、思想教育:历史上的今天 复习:复平面的点集 二、新课内容: (一)复变函数 定义 1:设 E 是复数 z x yi = + 的集合,若存在一个法则,按此法则对于 E 的每一个 z ,都 有一个(或多个)确定的复数 = +u iv 与之对应,那么就称 为 z 的复变函数。记 = f z( ) 。 集合 E 称为函数 = f z( ) 的定义集合,与 E 中 z 对应的 值构成的集合 E 称为函数值集合,记为 f (E) ,即 G = f (E) . 若 z 的一个值对应着 的一个值,则称复变函数 f (z) 是单值的;若 z 的一个值对应着 的两个 或两个以上的值,则称复变函数 f (z) 是多值的。 与点 zE 对应的点 = f z( ) 称为点 z 的像(Image),同时点 z 就为点 = f z( ) 的原像(Inverse) 例 1: 2 = z 是定义在整个复平面上的函数; z 1 = 是定义在除原点外的整个复平面上的复变函数。 z(z 1, n 2, n Z) n = ; = Argz(z 0) 均为 z 的多值函数。 例 2: z 1 = 将 z 平面上的直线 x =1 映射成 平面上的何种曲线? 解:设 z = x +iy, 2 2 x y x iy u iv + − = + = , x =1, 则 2 1 1 y iy + − = , , 1 1 2 y u + = 2 1 y y v + − = = + + = u y u v 2 2 2 1 1 4 1 ) 2 1 ( 2 2 u − + v = 。 反函数:设函数 = f z( ) 定义在 E 上,值域为 G 若对于 G 中的任一点 ,在 E 中存在一个或 几个点 z 与之对应,则在 G 上确定了一个单值或多值函数,记作 ( ) 1 − z = f ,称为 = f z( ) 的反 函数。若 = f z( ) 与它的反函数 ( ) 1 − z = f 都是单值的,那么称函数 = f z( ) 是一一对应的。 注:单值函数的反函数不一定是单值函数。 (二)复变函数的极限与连续 1、复变函数的极限 定义 2:设函数 = f z( ) 定义在 0 z 的去心邻域 z − z r 0 0 内。若存在常数 A,对于任意给 定的 0 ,都存在一正数 (0 r) ,使得当 z − z r 0 0 时,有 f (z) − A ,则称函数 f (z) 当 0 z → z 时的极限存在,常数 A 为其极限值,记作 f z A z z = → lim ( ) 0 。 定理 1:设 0 0 0 f (z) = u(x, y) +iv(x, y),z = x +iy , A= a +ib ,则 = → f z A z z lim ( ) 0 u x y a x y x y = → lim ( , ) ( , ) ( , ) 0 0 且 v x y b x y x y = → lim ( , ) ( , ) ( , ) 0 0 。 定理 2:极限四则运算法则(略) 例 3:判断下列函数在原点处的极限是否存在,若存在,试求出其极限值。 z z z f z Re( ) (1) ( ) = 2 2 Re( ) (2) ( ) z z f z = 2、复变函数的连续 定义 3:若 lim ( ) ( )0 0 f z f z z z = → 则称 f (z) 在 0 z 处连续。如果 f (z) 在区域 D 内每一点都连续,那 么函数 f (z) 在区域 D 内连续。 定理 3:若 f (z), g(z) 在点 0 z 处连续,则其和、差、积、商(分母不为零)在 0 z 处连续

定理4:若函数h=g(日)在点。处连续,函数p=∫()在点h。=g()处连续,则复合函数 =f(g(》在点:处连续。 定理5:设函数fe)=x,y)+(x,y),。=x+%,则fe)在点处连续的充要条件是 x,y),x,y)均在点(,)处连线。 例4:讨论函数argz的连续性。 解:(1)当z=0时,arg:无定义,因而不连续。 (2)当为负实轴上的点时,0=x0<0,则 lim(arctan= lim arg==lim arg== lim(arctan-)=- 因此,n为负实轴上的点时,arg:不连续。 (3)5为正、负虚轴上的点时,5o=少,06≠0)时,有lim arg:=± ,即arg:在虚轴上连续 (4)。=x,+%为其它点时, lim arg==arctan 为第一、四象限点,和实半轴上的点 lim arg:=arctano 2+π, 为第二象限点 marg:=arctan-之-不, ,为第三象限点 即arg:在复平面上除原点和负实轴外连续。 有界闭区域上的连续函数,一定在该闭区域上有界。 在闭曲线或包含曲线端点在内的曲线段上的连续函数f(:)在曲线上有界,即(:≤M, (三)解析函数的概念 1、复变函数的导数 定义4:设函数0=f(:)定义在:平面上区城D内,点o,26+△∈D, △ 处可导,这个极限值称为/(e)在:处的导数,记作∫代)=少回 do 。 2、解析函数的概念 若函数fe)在点。及:。的领域内处处可导,则称函数fe)在点:,解析,若函数f)在区域 D内每一点解析,则称函数f(:)在区域D内解析,或称f()是D内的解析函数。 若函数f(e)在D不解析,但在:。的任意邻域内总有f(a)的解析点,则称:。为f()的奇点。 注:函数(:)在区城D内解析与在区城内可导是等价的,但是函败在一点处解析和在一点处 可导并不等价: 三、课堂小结:本次课重点在于讲复变函数的极限和连续的概念,及解析函数的概念。(要 求下去多看书, 理 解概念)。布置作业:完成《复变函数与积分变换》 学生工作任务单(5) 五.课后小结:
定理 4:若函数 h = g(z) 在点 0 z 处连续,函数 = f (h) 在点 ( ) 0 0 h = g z 处连续,则复合函数 = f (g(z)) 在点 0 z 处连续。 定理 5:设函数 f (z) = u(x, y) +iv(x, y) , 0 0 0 z = x +iy ,则 f (z) 在点 0 z 处连续的充要条件是 u(x, y),v(x, y) 均在点 ( , ) 0 0 x y 处连续。 例 4:讨论函数 arg z 的连续性。 解:(1)当 z = 0 时, arg z 无定义,因而不连续。 (2)当 0 z 为负实轴上的点时, z0 = x0 0,则 − = − + = = = − − → → → → → → lim (arctan ) lim (arctan ) lim arg lim arg , 0 , 0 ( , ) ( ,0) 0 0 0 0 x y x y z z x x y x x y z z x y x 因此, 0 z 为负实轴上的点时, arg z 不连续。 (3) 0 z 为正、负虚轴上的点时, ( 0) z0 = iy0 y0 时,有 2 lim arg 0 = → z z z ,即 arg z 在虚轴上连续 (4) 0 0 0 z = x +iy 为其它点时, 为第三象限点 为第二象限点 为第一、四象限点,和实半轴上的点 0 0 0 0 0 0 0 0 0 lim arg arctan , lim arg arctan , lim arg arctan , 0 0 0 z z z x y z x y z x y z z z z z z z = − = + = → → → 即 arg z 在复平面上除原点和负实轴外连续。 有界闭区域上的连续函数,一定在该闭区域上有界。 在闭曲线或包含曲线端点在内的曲线段上的连续函数 f (z) 在曲线上有界,即 f (z) M . (三)解析函数的概念 1、复变函数的导数 定义 4:设函数 = f (z) 定义在 z 平面上区域 D 内,点 z0 ,z0 +zD , ( ) ( ) 0 0 = f z +z − f z ,若极限 z f z z f z z z z + − = → → ( ) ( ) lim lim 0 0 0 0 存在,则称函数 f (z) 在点 0 z 处可导,这个极限值称为 f (z) 在 0 z 处的导数,记作 0 0 ( ) ( )0 z z dz z z d dz df z f z = = = = 。 2、解析函数的概念 若函数 f z( ) 在点 0 z 及 0 z 的领域内处处可导,则称函数 f z( ) 在点 0 z 解析,若函数 f z( ) 在区域 D 内每一点解析,则称函数 f z( ) 在区域 D 内解析,或称 f z( ) 是 D 内的解析函数。 若函数 f z( ) 在 D 不解析,但在 0 z 的任意邻域内总有 f z( ) 的解析点,则称 0 z 为 f z( ) 的奇点。 注:函数 f z( ) 在区域 D 内解析与在区域内可导是等价的,但是函数在一点处解析和在一点处 可导并不等价。 三、课堂小结:本次课重点在于讲复变函数的极限和连续的概念,及解析函数的概念。(要 求下去多看书,理解概念)。布置作业:完成《复变函数与积分变换》学生工作任务单(5) 五.课后小结: x y 0 z

克拉玛依职业技术学院教案 教案序号: 05课型: 理论授课时间:2022-10-3 班级:测控2141班 教材:《复变函数与积分变换》 网络学习条件:安静的环境,网络通畅学生人数:29 教学设备安全情况: 教学安全要求: 一、课题: 第二章解析函数 §2-3、4函数可导与解析的充要条件初等函数 二、教学目的: 1.理解和掌握函数可导与解析的充要条件及初等函数: 2.熟练掌握函数可导与解析的充要条件及初等函数。 三、教学重点和疑、难点: 重点:(1)函数可导与解析的充要条件(2)初等函数 难点:(1〉函数可导与解析的充要条件(2〉初等函数。 四.教学过程及教学内容安排 教学内容 时间分配 二 思想教育与复习 二、新课内容 (一)函数可导与解析的充要条件 (50分) (二)初等函数 (35分) 三、课堂小结 5分 布置作业 0 一、思想教育:柯西一黎曼方程的产生
克拉玛依职业技术学院教案 教案序号: 05 课型: 理论 授课时间: 2022- 10 -3 班级: 测控 2141 班 教材: 《复变函数与积分变换》 网络学习条件:安静的环境,网络通畅学生人数:_29_ 教学设备安全情况:_ 教学安全要求:_ _ 一、课题: 第二章 解析函数 §2-3、4 函数可导与解析的充要条件 初等函数 二、教学目的: 1. 理解和掌握函数可导与解析的充要条件及初等函数; 2. 熟练掌握函数可导与解析的充要条件及初等函数。 三、教学重点和疑、难点: 重点:〈1〉函数可导与解析的充要条件〈2〉初等函数。 难点:〈1〉函数可导与解析的充要条件〈2〉初等函数。 四.教学过程及教学内容安排 教学内 容 时间分配 一、 思想教育与复习 二、新课内容 (一)函数可导与解析的充要条件 (二)初等函数 10 分 75 分 (50 分) (35 分) 三、 课堂小结 布置作业 5 分 内 容 一、思想教育:柯西-黎曼方程的产生

复习:复变函数的极限与连续与可导 二、新课内容 (一)函数可导与解析的充要条件 1、柯西黎曼方程(CR方程): 对与二元实函数训化,),K,川,方程-=-产称为0R方程。 dxav'ov ax 定理7:设函数f()=x,)+(,)在区域D内有定义,则f)在区域D内一点 二=x+少可导的充要条件是: (1)二元实函数u(x,y),(x,y)在点(x,y)处可微; (2)二元实函数(x,y),(x,)在点(x,y)满足C方程。 定理8:设函数f()=x,y)+i(x,y)在区域D内解析的充要条件是: (1)二元实函数(x,y),(x,y)在D内可微; (2)二元实函数4(x,),(xy)在D内满足CR方程。 推论1.1:若u(x,y)与(x,y)的一阶偏导在点(x,y)存在而且连续,并满足CR方程,则f(:) 在点(x,y)可导。 推论1.2:若(x,y)与(x,)的一阶偏导在区域内存在而且连续,并满足C方程,则f() 在区域D内解析 例1:讨论下列函数的可导性与解析性: (1)f(=)=Im(=) (2)fe)=f: 结论:()f(e)=m()在复平面上处处不可导,处处不解析。 (2)f()=:仅在(0,0)处可导。 例2:试证明函数fe)=e'(cosy+isiny)在:平面上解析,且f(e)=fe). 例3证明0方指能版坐振彩流是空高容一治 1 Cu (三)初等函数 1、指数函数:=x+y 形式 三角形式 实部 虚部 辐角 e"(cosy+isiny)e"cosy e"siny Arg(e)=y+2kπ 可导 运算法则 周期性 r-00 模 (e')'=e 2司 不存在 e 单值函数 e12 e 例4:计算下列各式的值: 0)e2 (2)e-24 (3) 答案:()e2=e2(cosl+isinl) (2)e-2r=e2a 22
复习:复变函数的极限与连续与可导 二、新课内容 (一)函数可导与解析的充要条件 1、柯西-黎曼方程(C-R 方程): 对与二元实函数 u(x, y) ,v(x, y) ,方程 x v y u y v x u = − = , 称为 C-R 方程。 定理 7:设函数 f (z) = u(x, y) +iv(x, y) 在区域 D 内有定义,则 f (z) 在区域 D 内一点 z = x +iy 可导的充要条件是: (1)二元实函数 u(x, y) ,v(x, y) 在点 (x, y) 处可微; (2)二元实函数 u(x, y) ,v(x, y) 在点 (x, y) 满足 C-R 方程。 函数的导数公式: ( ) u v v v v u u u f z i i i i x x y x y y x y = + = + = − = − 定理 8:设函数 f (z) = u(x, y) +iv(x, y) 在区域 D 内解析的充要条件是: (1)二元实函数 u(x, y) ,v(x, y) 在 D 内可微; (2)二元实函数 u(x, y) ,v(x, y) 在 D 内满足 C-R 方程。 推论 1.1:若 u(x, y) 与 v(x, y) 的一阶偏导在点 (x, y) 存在而且连续,并满足 C-R 方程,则 f z( ) 在点 (x, y) 可导。 推论 1.2:若 u(x, y) 与 v(x, y) 的一阶偏导在区域内存在而且连续,并满足 C-R 方程,则 f z( ) 在区域 D 内解析 例 1:讨论下列函数的可导性与解析性: (1) ( ) Im( ) f z z = 2 (2) ( ) f z z z = 结论: (1) ( ) Im( ) f z z = 在复平面上处处不可导,处处不解析。 2 (2) ( ) f z z z = 仅在(0,0)处可导。 例 2: 试证明函数 ( ) (cos sin ) x f z e y i y = + 在 z 平面上解析,且 f z f z ( ) ( ) = 。 例 3:证明 C-R 方程的极坐标形式是 1 1 , u v v u r r r r = = − (三)初等函数 1、指数函数 z x iy = + 指数函数 exp(z) 形式 三角形式 实部 虚部 辐角 z x iy e e + = (cos sin ) x e y i y + cos x e y sin x e y ( ) 2 z Arg e y k = + 可导 运算法则 周期性 x → 模 单值函数 ( )z z e e = 1 2 1 2 z z z z e e e + = 1 1 2 2 z z z z e e e − = 2i 不存在 x e 例 4:计算下列各式的值: 2 (1) i e + 2( ) (2) i x iy e − + 2 3 (3) i e − 答案: 2 2 (1) (cos1 sin1) i e e i + = + 2( ) 2 (2) i x iy x e e − + − = 2 2 2 3 3 3 1 3 (3) (cos( ) sin( )) ( ) 3 3 2 2 i e e i e i − − − = + = −
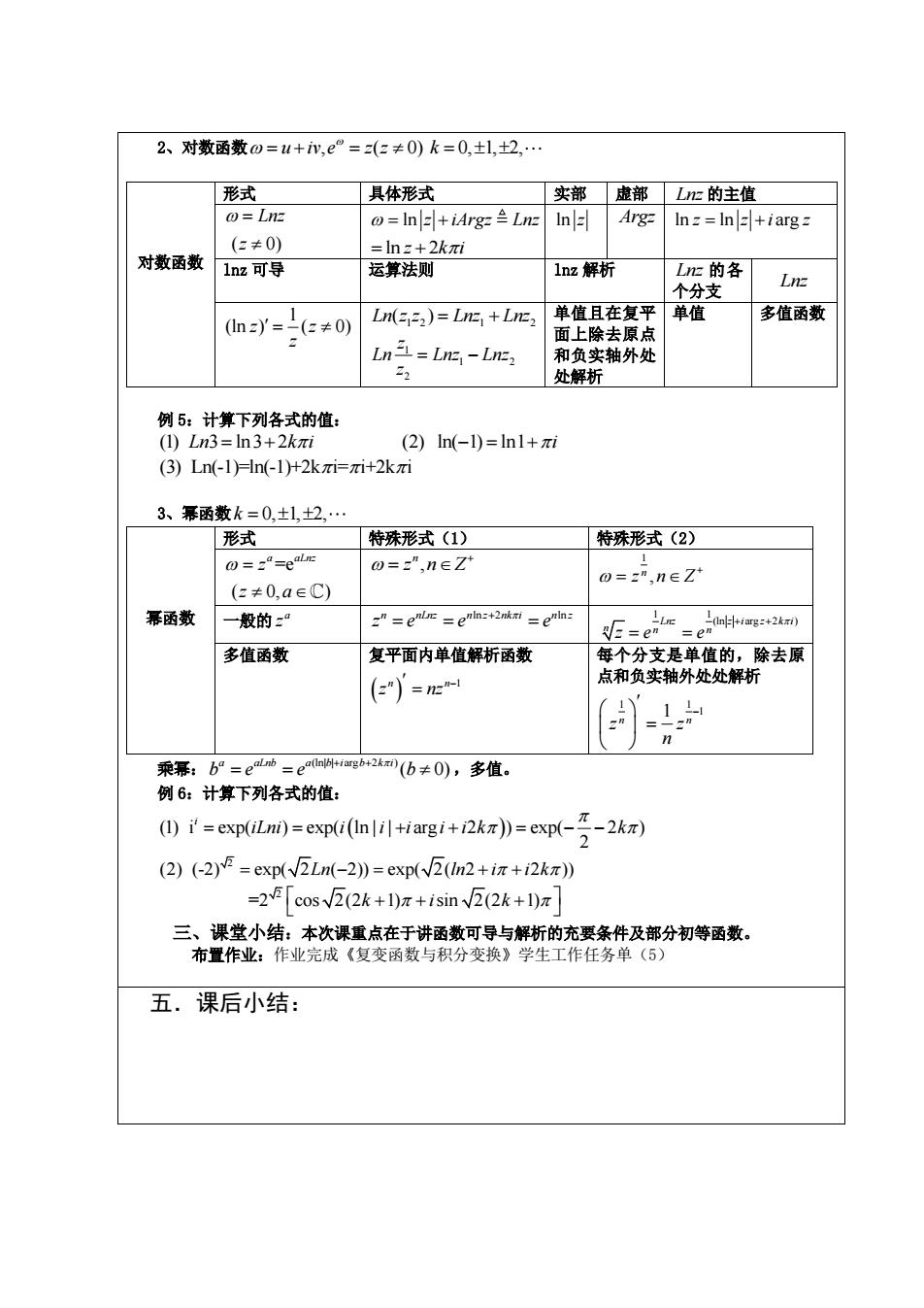
2、对数函数0=1+i,.e”=(:≠0)k=0,±1,±2. 形式 具体形式 实部虚部L:的主值 =L In z Arg- Inz =In +iarg (=≠0】 =ln-+2kπi 对数函数 1nz可导 运算法则 1nz解析 LUx的各 个分支 Lnz 0ny=e≠0 Ln()=Lm+Lm 单值且在复平 单值 多值函数 ,-Inz: 面上除去原点 2 和负实轴外处 处解析 例5: 计算下列各式的值 (①)Ln3=ln3+2kπi (2)In(-1)=Inl+zi (3)Ln(-1)=In(-1)+2kxi=+2ki 3、幂函数k=0,±1,2, 形式 特殊形式(1) 特殊形式(2) @=2-ealm @=2",neZ' 0=:",nEZ (e≠0,aeC) 幂函数 一般的: E=e=e4tgan 多值函数 复平面内单值解析函数 每个分支是单值的,除去原 (e)=x 点和负实轴外处处解析 乘幂:b=eb=ea4 (b≠0),多值。 例6:计算下列各式的值 0=*=exp(+2kr》=ep-2k (2)(2)=exp(Ln(-2))=exp((Imn2+iz+i2k)) =2cosv2(2k+1)+isin2(2k+1)z 三、课堂小结:本次课重点在于讲函数可导与解析的充要条件及部分初等函数。 布置作业:作业完成《复变函数与积分变换》学生工作任务单(5) 五.课后小结:
2、对数函数 u iv e z z , ( 0) = + = k = 0, 1, 2, 对数函数 形式 具体形式 实部 虚部 Lnz 的主值 ( 0) Lnz z = = + ln z iArgz Lnz = + ln 2 z k i ln z Argz ln ln arg z z i z = + lnz 可导 运算法则 lnz 解析 Lnz 的各 个分支 Lnz 1 (ln ) ( 0) z z z = 1 2 1 2 Ln z z Lnz Lnz ( ) = + 1 1 2 2 z Ln Lnz Lnz z = − 单值且在复平 面上除去原点 和负实轴外处 处解析 单值 多值函数 例 5:计算下列各式的值: (1) 3 ln3 2 Ln k i = + (2) ln( 1) ln1 − = +i (3) Ln(-1)=ln(-1)+2k i= i+2k i 3、幂函数 k = 0, 1, 2, 幂函数 形式 特殊形式(1) 特殊形式(2) =e ( 0, ) a aLnz z z a = , n z n Z+ = 1 , n z n Z + = 一般的 a z n nLnz n z nk i n z ln 2 ln z e e e + = = = 1 1 Lnz z i z k i (ln arg 2 ) n n n z e e + + = = 多值函数 复平面内单值解析函数 ( ) n n 1 z nz − = 每个分支是单值的,除去原 点和负实轴外处处解析 1 1 1 1 n n z z n − = 乘幂: (ln| | arg 2 ) ( 0) a aLnb a b i b k i b e e b + + = = ,多值。 例 6:计算下列各式的值: (1) i exp( ) exp( ln | | arg 2 ) exp( 2 ) ( ) 2 i iLni i i i i i k k = = + + = − − 2 (2) (-2) exp( 2 ( 2)) exp( 2( 2 2 )) = − = + + Ln ln i i k 2 =2 cos 2(2 1) sin 2(2 1) k i k + + + 三、课堂小结:本次课重点在于讲函数可导与解析的充要条件及部分初等函数。 布置作业:作业完成《复变函数与积分变换》学生工作任务单(5) 五.课后小结: