随机误差的分布服从正态分布 如测定次数较多,在系统误差已经排除的情况下,随机误差的分布也有一 定的规律,如以横坐标表示随机误差的值,纵坐标表示误差出现的概率大小,当 测定次数无限多时,划得随机误差正态分布曲线,见图2一2。 上1 图2-2标准正态分布曲线 定义 (2-11) 随机误差分布具有以下性质: (1)对称性:大小相近的正误差和负误差出现的概率相等,误差分布曲线是 对称的。 (2)单峰性:小误差出现的概率大,大误差出现的概率小,很大误差出现的 概率非常小。误差分布曲线只有一个峰值。误差有明显的集中趋势。 (3)有界性:仅仅由于偶然误差造成的误差不可能很大,即大误差出现的概 率很小。如果发现误差很大的测定值出现,往往是由于其他过失误差造成 时,对这种数据应作相应的处理。 (4)抵偿性:误差的算术平均值的极限为零 (2-12) 在标准正态分布曲线上,如把曲线与横华标从O至+O之间所句相的面 积代表所有随机误差出现的概率的总和)定为100%,通过计算发现误差范围 与出现的概率有如下关系(见表2一1和图2一2)。 表2-1误差在某些区间出现的概率 Y-" [=g,+8] 【-1,1] 68.3% [-1.96a,+1.960] [-1.96,+1.96 95% -2a,+2c “2+ [-3a,+3 3.+3 99.7%
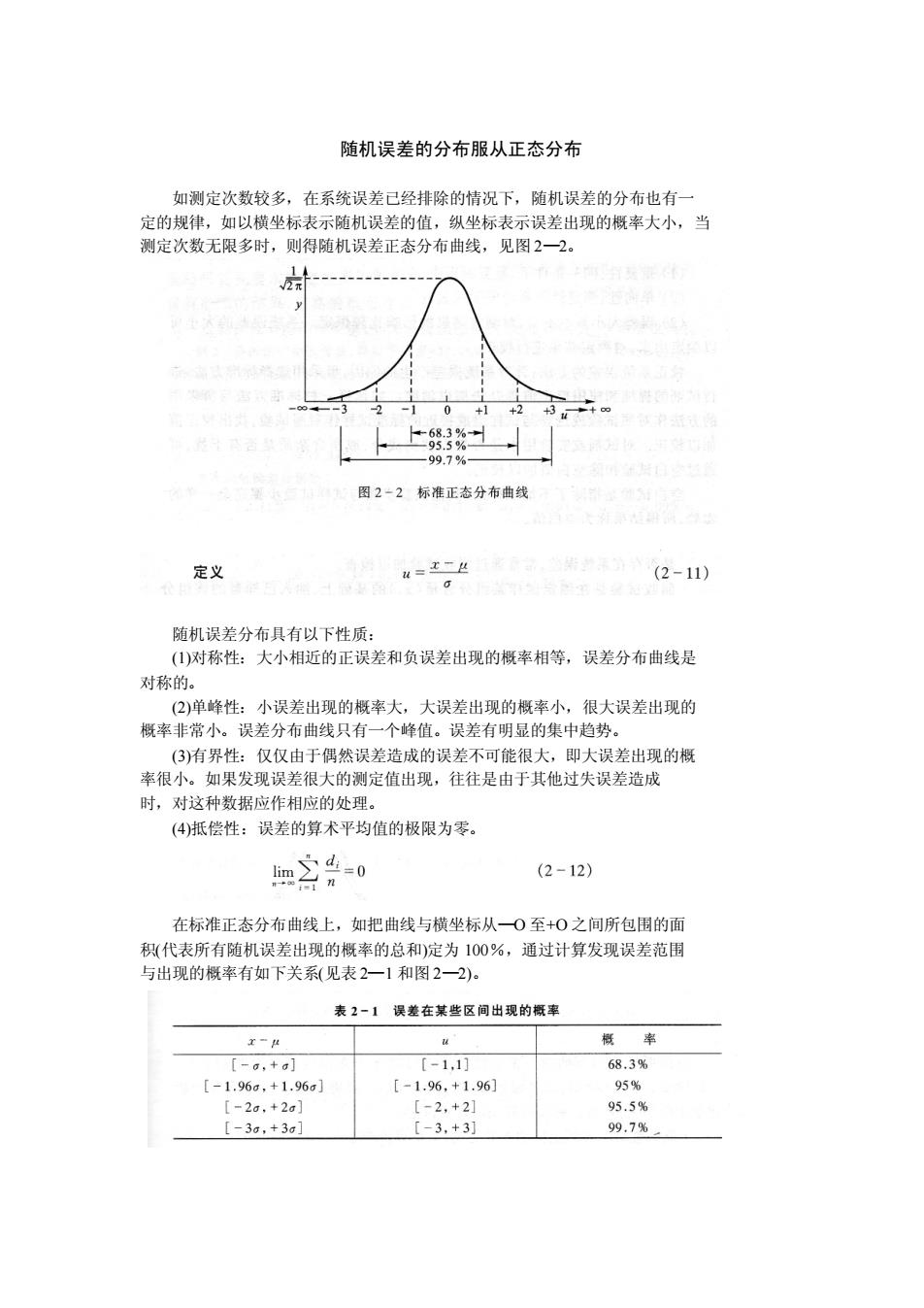
随机误差的分布服从正态分布 如测定次数较多,在系统误差已经排除的情况下,随机误差的分布也有一 定的规律,如以横坐标表示随机误差的值,纵坐标表示误差出现的概率大小,当 测定次数无限多时,则得随机误差正态分布曲线,见图 2—2。 随机误差分布具有以下性质: (1)对称性:大小相近的正误差和负误差出现的概率相等,误差分布曲线是 对称的。 (2)单峰性:小误差出现的概率大,大误差出现的概率小,很大误差出现的 概率非常小。误差分布曲线只有一个峰值。误差有明显的集中趋势。 (3)有界性:仅仅由于偶然误差造成的误差不可能很大,即大误差出现的概 率很小。如果发现误差很大的测定值出现,往往是由于其他过失误差造成 时,对这种数据应作相应的处理。 (4)抵偿性:误差的算术平均值的极限为零。 在标准正态分布曲线上,如把曲线与横坐标从—O 至+O 之间所包围的面 积(代表所有随机误差出现的概率的总和)定为 100%,通过计算发现误差范围 与出现的概率有如下关系(见表 2—1 和图 2—2)
测定值或误差出现的概率称为置信度或置信水平(confidence level),图 2一2中68.3%,95.5%,99.7%即为置信度,其意义可以理解为某一定范围的测 定值(或误差值)出现的概率。 +2 3o等称为置信区间(confi denceinterval),其意义为真实值在指定概率下,分布在某一个区间。置信度选 得高,置信区间就宽。 有限次测定中随机误差服从‘分布 在分析测试中,测定次数是有限的,一般平行测定3~5次 无法计算总体 标准差σ和总体平均值,而有限次测定的随机误差并不完全服从正态分布,而 是服从类似于正态分布的t分布,t分布是由英国统计学家与化学家 骨,代。提,以的笔名发表,:的定又与一V。-我风足 t=1 (2-13) 也可衍生出 t=所 (2-14) 分布曲线如图2一3所示。 八) 0.4 (a5 图2-3t分布曲线 而变,当20时, 二者很近似,当f一∞时, 化学中应用很多,将在后面的有关内容中讨论。 【值与置信度和测定值的次数有关,其值可由表2一2中查得
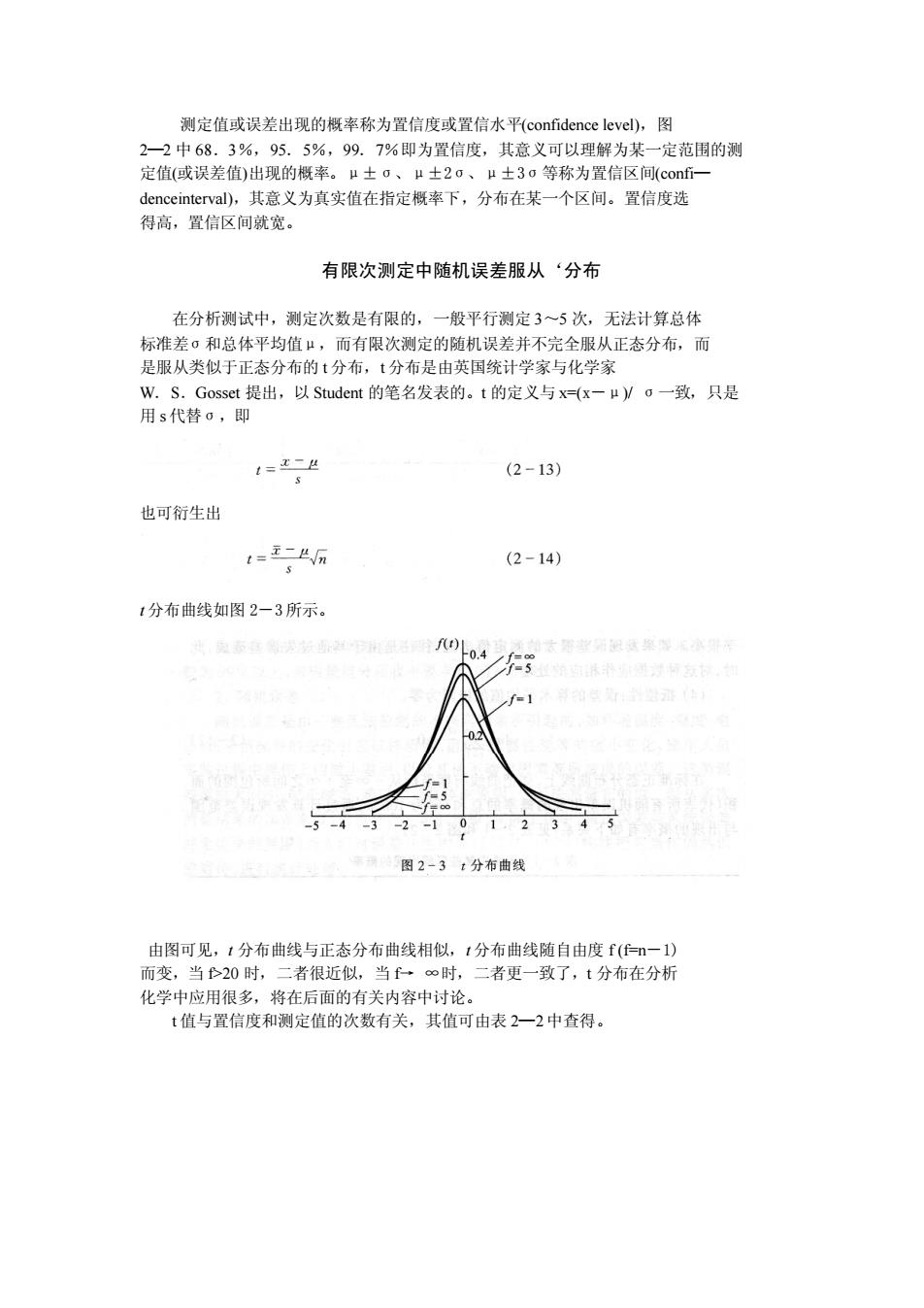
测定值或误差出现的概率称为置信度或置信水平(confidence level),图 2—2 中 68.3%,95.5%,99.7%即为置信度,其意义可以理解为某一定范围的测 定值(或误差值)出现的概率。μ±σ、μ±2σ、μ±3σ等称为置信区间(confi— denceinterval),其意义为真实值在指定概率下,分布在某一个区间。置信度选 得高,置信区间就宽。 有限次测定中随机误差服从‘分布 在分析测试中,测定次数是有限的,一般平行测定 3~5 次,无法计算总体 标准差σ和总体平均值μ,而有限次测定的随机误差并不完全服从正态分布,而 是服从类似于正态分布的 t 分布,t 分布是由英国统计学家与化学家 W.S.Gosset 提出,以 Student 的笔名发表的。t 的定义与 x=(x-μ)/ σ一致,只是 用 s 代替σ,即 也可衍生出 t 分布曲线如图 2-3所示。 由图可见,t 分布曲线与正态分布曲线相似,t 分布曲线随自由度 f (f=n-1) 而变,当 f>20 时,二者很近似,当 f→ ∞时,二者更一致了,t 分布在分析 化学中应用很多,将在后面的有关内容中讨论。 t 值与置信度和测定值的次数有关,其值可由表 2—2中查得