第一节运输问题及其数学模型 铁厂 铁 B. B4产量 2 6 8 2 8 3 7 销量 5 表3-2例1的运输数据表 13
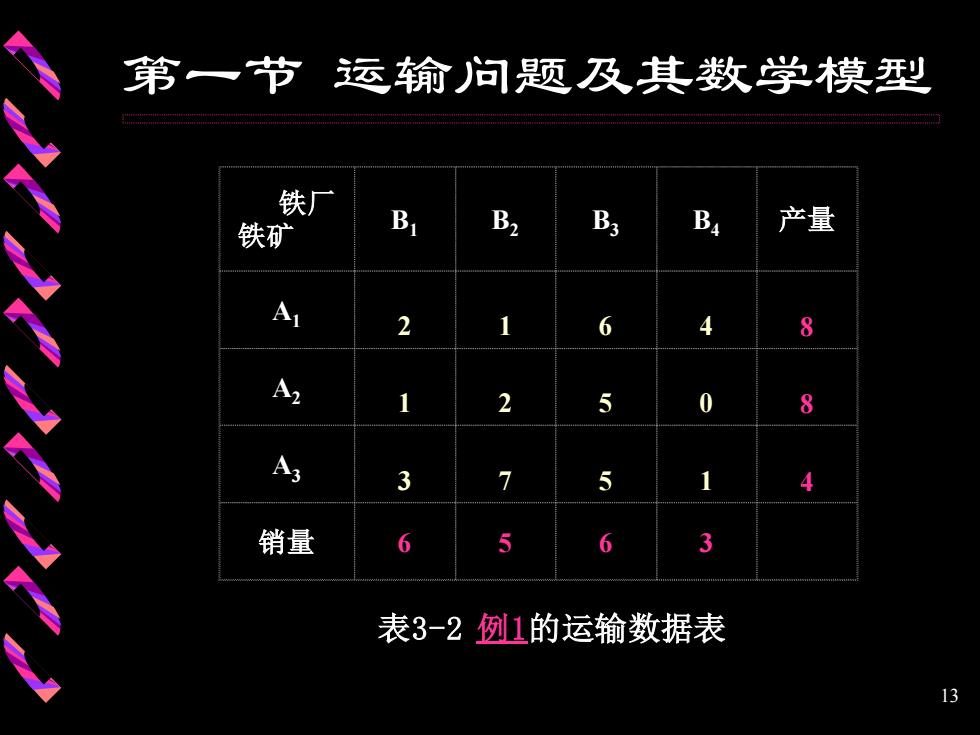
13 第一节 运输问题及其数学模型 表3-2 例1的运输数据表 铁厂 铁矿 B1 B2 B3 B4 产量 A1 2 1 6 4 8 A2 1 2 5 0 8 A3 3 7 5 1 4 销量 6 5 6 3

第一节运输问题及其数学模型 这是一个3个产地,4个销地,产销平衡的运 输问题,它属于模型3-2),是一个线性规划模 型。虽然可以利用求解线性规划的单纯形法进行 求解,但是,由于变量很多求解也还是比较困难 的。当然,也可以用LNGO求解。然而, 这两种 解法都没有充分利用运输问题本身的特点。运输 问题自身的特点是:技术系数都是0或1,每列只 有两个1;约束都是等式;产销平衡。下面我们 来寻找一种特殊的解法。 14
14 第一节 运输问题及其数学模型 这是一个3个产地,4个销地,产销平衡的运 输问题,它属于模型(3-2),是一个线性规划模 型。虽然可以利用求解线性规划的单纯形法进行 求解,但是,由于变量很多求解也还是比较困难 的。当然,也可以用LINGO求解。然而,这两种 解法都没有充分利用运输问题本身的特点。运输 问题自身的特点是:技术系数都是0或1,每列只 有两个1;约束都是等式;产销平衡。下面我们 来寻找一种特殊的解法。 p

第二节求解运输问题表上作业法 运输问题基变量的个数 对于产销平衡的运输问题(3-2),由于有 (3-1)式成立,所以相应的系数矩阵的秩为 m+n-1。假设前面例1的决策变量按: ×11,×12,X13,X14×21×22×23,×24X31,X32,X33,X34 b 排列,则相应的系数矩阵为(接着进行初等行变 换) 15
15 第二节 求解运输问题表上作业法 一、运输问题基变量的个数 对于产销平衡的运输问题(3-2),由于有 (3-1)式成立,所以相应的系数矩阵的秩为 m+n-1。假设前面例1的决策变量按: x11,x12,x13,x14,x21,x22,x23,x24,x31,x32,x33,x34 b 排列,则相应的系数矩阵为(接着进行初等行变 换):

第二节求解运输问题表上作业法 111 8 1111 8 1111 4 1 6 1 1 5 1 1 6 1 1 3 1111 8 1111 8 1111 4 0-1-1-11 1 -2 1 1 5 1 1 1 6 1 1 1 3 16
16 第二节 求解运输问题表上作业法 3 6 5 6 4 8 8 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 → − − − − 3 6 5 2 4 8 8 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 →

第二节求解运输问题表上作业法 1 1 8 1111 8 1111 4 00-1-111 11 3 1 1 5 1 1 6 1 3 111 8 1111 8 1111 4 0 00-1111 1 1 9 1 1 1 5 1 1 1 6 1 1 1 3 17
17 第二节 求解运输问题表上作业法 − − 3 6 5 3 4 8 8 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 → − 3 6 5 9 4 8 8 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 →