
第一章 线性规戈划及单纯形法 线性规划问题及其数学模型 线性规划的解及其性质 解线性规划的单纯形法 单纯性法的进一步讨论 线性规划应用举例 3
3 第一章 线性规划及单纯形法 线性规划问题及其数学模型 线性规划的解及其性质 解线性规划的单纯形法 单纯性法的进一步讨论 线性规划应用举例

第一节线性规划问题及其数学模型 线性规划问题及其数学模型 1)线性规划问题的提出 例1(范例:产品配比问题)某工厂计划生 产甲、乙两种适销产品,每件利润分别为3百元 和5百元。甲、乙产品的部件各自在A、B两个车 间分别生产,每件甲、乙产品的部件分别需要A、 B车间的生产能力为1个工时和2个工时;两种产 品的部件最后都要在C车间装配,装配每件甲、 乙产品分别需要3工时和4工时 4
4 第一节 线性规划问题及其数学模型 一、线性规划问题及其数学模型 1)线性规划问题的提出 例1(范例:产品配比问题)某工厂计划生 产甲、乙两种适销产品,每件利润分别为3百元 和5百元。甲、乙产品的部件各自在A、B两个车 间分别生产,每件甲、乙产品的部件分别需要A、 B车间的生产能力为1个工时和2个工时;两种产 品的部件最后都要在C车间装配,装配每件甲、 乙产品分别需要3工时和4工时

第一节线性规划问题及其数学模型 假设A、B、C三个车间每天可用于生产这两 种产品的工时数分别为8、12和36。问应如何安排 生产这两种产品才能获利最多? 解:这是一个典型的产品配比问题。因为 甲、乙两种产品需要争用C车间的有限能力。因 此就有一个如何搭配两种产品的产量,才能充分 发挥生产能力而获利最多的问题。 5
5 第一节 线性规划问题及其数学模型 假设A、B、C三个车间每天可用于生产这两 种产品的工时数分别为8、12和36。问应如何安排 生产这两种产品才能获利最多? 解: 这是一个典型的产品配比问题。因为 甲、乙两种产品需要争用C车间的有限能力。因 此就有一个如何搭配两种产品的产量,才能充分 发挥生产能力而获利最多的问题

第一节线性规划问题及其数学模型 现在来建立这个问题的数学模型。假设x1、 x2分别为甲、乙产品的日产量,Z为这两种产品 每天的总利润。下面先列出该问题的数据表: 6
6 第一节 线性规划问题及其数学模型 现在来建立这个问题的数学模型。假设x1、 x2分别为甲、乙产品的日产量,Z为这两种产品 每天的总利润。下面先列出该问题的数据表:
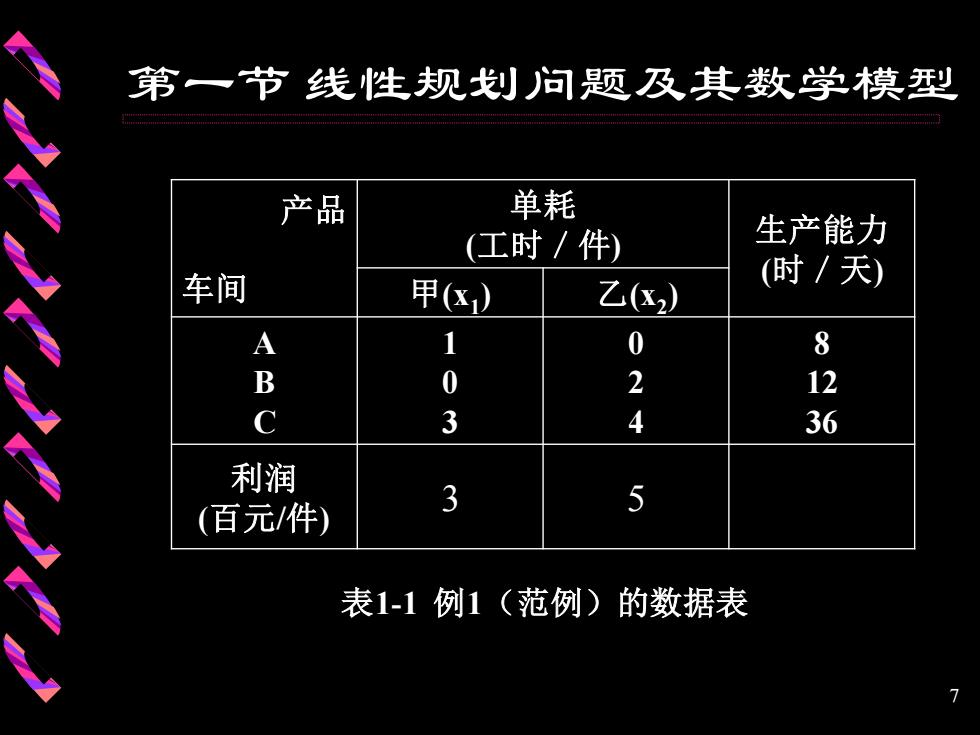
第一节线性规划问题及其数学模型 产品 单耗 (工时/件) 生产能力 车间 (时/天) 甲() 乙(2) A 1 0 8 B 0 2 12 C 3 4 36 利润 3 5 (百元/件) 表1-1例1(范例)的数据表 7
7 表1-1 例1(范例)的数据表 第一节 线性规划问题及其数学模型 产品 车间 单耗 (工时/件) 生产能力 (时/天) 甲(x1 ) 乙(x2 ) A B C 1 0 3 0 2 4 8 12 36 利润 (百元/件) 3 5