
第八章 图图与网络分析 图的基本概念 最小树问题 最短路问题 最大流问题 最小费用流问题 中国邮路问题 3
3 第八章 图与网络分析 图的基本概念 最小树问题 最短路问题 最大流问题 最小费用流问题 中国邮路问题

当我们在研究某些现实系统时,如果系统中 含有有限个待研究的对象,除了关心这些对象本 身的特性,同时还要考虑对象之间的相互关系 一个比较简单并且是常用的方法就是画一张图 用点表示系统中的对象,用点之间的连线表示对 象之间的相互关系。通过对图的研究,达到研究 系统的目的。例如我们经常见到的道路交通图 管道网络图、工程计划图等。用图来表达和研究 个系统往往具有直观、简洁和方便等特点。 4
4 引 言 当我们在研究某些现实系统时,如果系统中 含有有限个待研究的对象,除了关心这些对象本 身的特性,同时还要考虑对象之间的相互关系, 一个比较简单并且是常用的方法就是画一张图, 用点表示系统中的对象,用点之间的连线表示对 象之间的相互关系。通过对图的研究,达到研究 系统的目的。例如我们经常见到的道路交通图、 管道网络图、工程计划图等。用图来表达和研究 一个系统往往具有直观、简洁和方便等特点

引言 图论(Graph Theory)是运筹学的一个重要分 支,它是建立和处理离散数学模型的一个重要工 具。 图论的研究最早可追溯到著名的哥尼斯堡七 桥问题。18世纪欧洲的哥尼斯堡城有一条流经全 城的普雷格尔河,河的两岸和河中两个小岛有七 座桥彼此相通(如图8-1所示)。 5
5 引 言 图论(Graph Theory)是运筹学的一个重要分 支,它是建立和处理离散数学模型的一个重要工 具。 图论的研究最早可追溯到著名的哥尼斯堡七 桥问题。18世纪欧洲的哥尼斯堡城有一条流经全 城的普雷格尔河,河的两岸和河中两个小岛有七 座桥彼此相通(如图8-1所示)
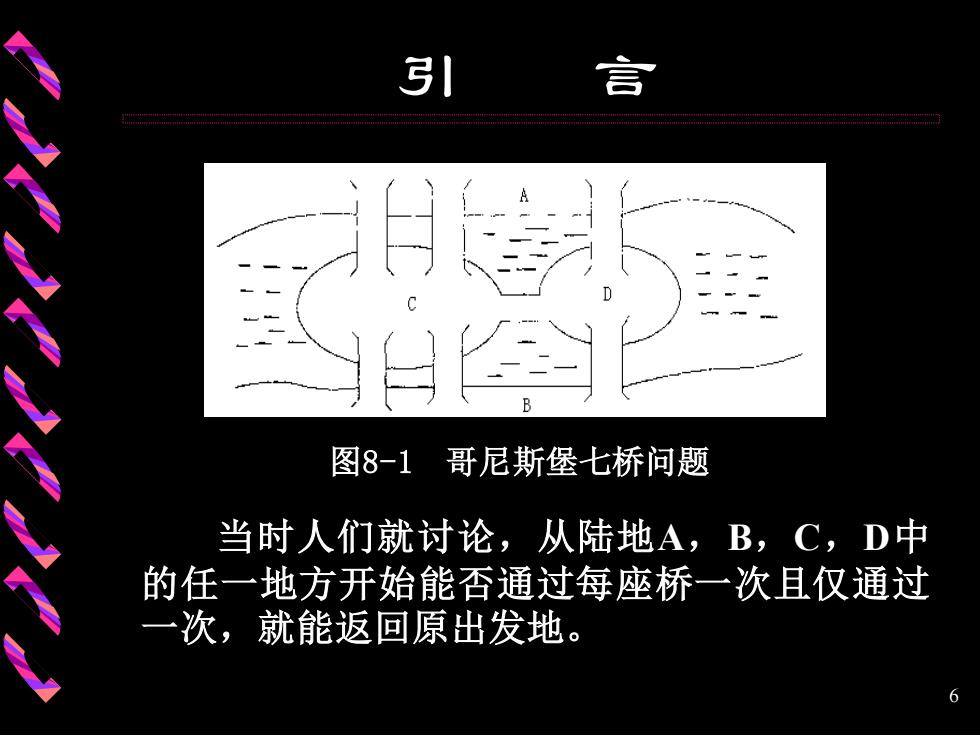
3引 言 、 图8-1 哥尼斯堡七桥问题 当时人们就讨论,从陆地A,B,C,D中 的任一地方开始能否通过每座桥一次且仅通过 一次,就能返回原出发地。 6
6 引 言 图8-1 哥尼斯堡七桥问题 当时人们就讨论,从陆地A,B,C,D中 的任一地方开始能否通过每座桥一次且仅通过 一次,就能返回原出发地
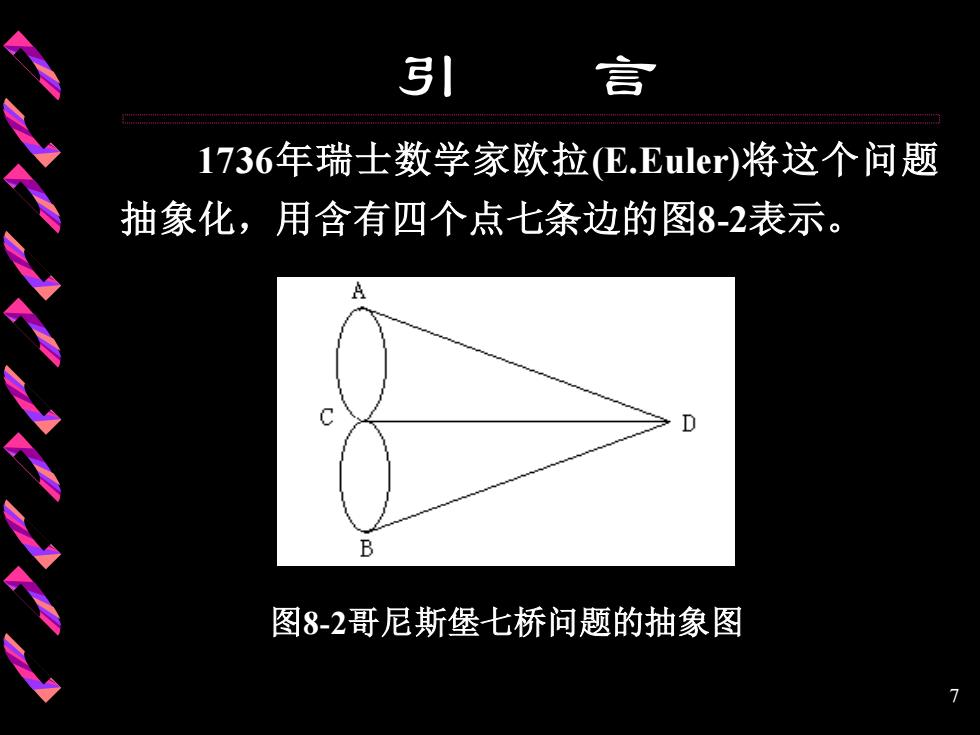
引 言 1736年瑞士数学家欧拉E.Euler)将这个问题 抽象化,用含有四个点七条边的图8-2表示。 B 图8-2哥尼斯堡七桥问题的抽象图 7
7 引 言 1736年瑞士数学家欧拉(E.Euler)将这个问题 抽象化,用含有四个点七条边的图8-2表示。 图8-2哥尼斯堡七桥问题的抽象图