
第一节运输问题及其数学模型 这是由多个产地供应多个销地的单品种商品 运输问题。为直观起见,可列出该问题的运输数 据表,如表3-1所示。表中的c为A运往B,单位 商品的运价 我们设变量x时(i=1,2,.,n;j1, 2, ,m)为由产地A:运往销地B,的商品数量, 如果运输问题的总产量等于其总销量,即有: 3-1 8
8 第一节 运输问题及其数学模型 这是由多个产地供应多个销地的单品种商品 运输问题。为直观起见,可列出该问题的运输数 据表,如表3-1所示。表中的cij为Ai运往Bj单位 商品的运价。 我们设变量xij (i=1,2,.,n;j=1, 2,.,m)为由产地Ai运往销地Bj的商品数量, 如果运输问题的总产量等于其总销量,即有: = = = m i n j ai bj 1 1 (3-1)
第一节运输问题及其数学模型 销地B1B2 B。产量 产地 11 12 10 a 21 22 2n a m m m2 mn m 销量 表3-1运输数据表(单价) 9
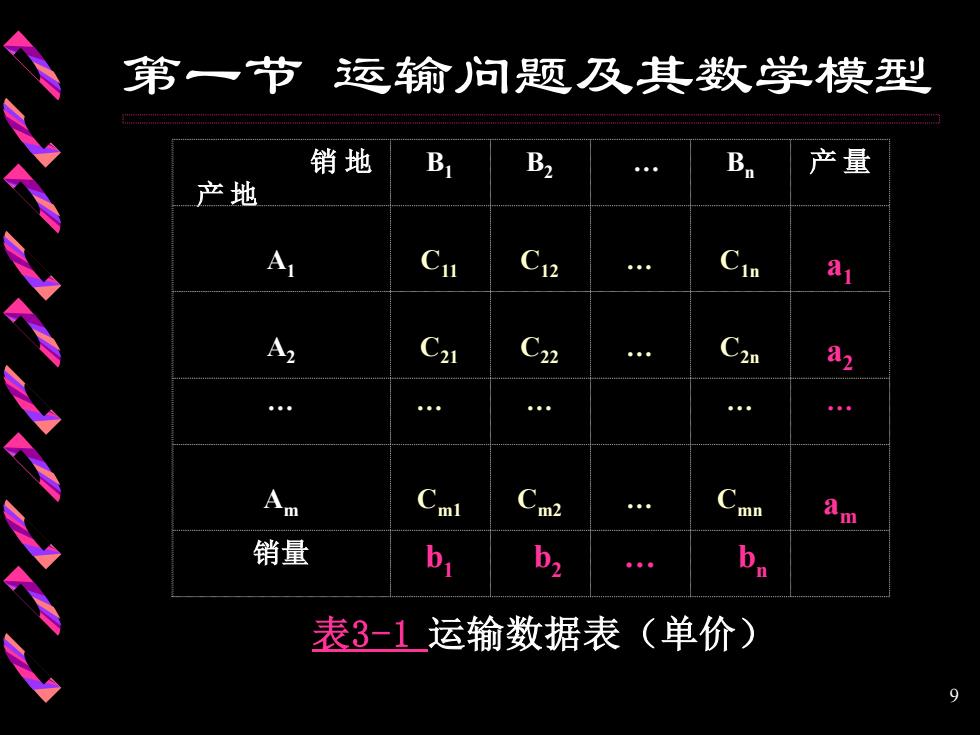
9 第一节 运输问题及其数学模型 表3-1 运输数据表(单价) 销 地 产 地 B1 B2 . Bn 产 量 A1 C11 C12 . C1n a1 A2 C21 C22 . C2n a2 . . . . . Am Cm1 Cm2 . Cmn am 销量 b1 b2 . bn

第一节运输问题及其数学模型 则称该运输问题为产销平衡的运输问题;反 之,称为产销不平衡的运输问题 0 产销平衡运输问题的数学模型可表示如下: n minz=∑cx i=1i=1 ∑xj=a: i=1,2,.,m xij=bi j=1,2,.,m 3-2) i=l x≥0, i=1,2,.,m;j=1,2,.,n 10
10 第一节 运输问题及其数学模型 则称该运输问题为产销平衡的运输问题;反 之,称为产销不平衡的运输问题。 产销平衡运输问题的数学模型可表示如下: = = = = = = = = = = = x i m j n x b j n x a i m Z c x i j m i i j j n j i j i m i n j i j i j 0, 1,2, , ; 1,2, , 1,2, , 1,2, , min 1 1 1 1 (3-2)

第一节运输问题及其数学模型 在模型(3-2)式中, 约束条件右侧常数a:和b; 满足(3-1)式。 在模型(3-2)中,目标函数表示运输总费用 极小化;前m个约束条件表示由某一产地运往各 个销地的商品数量之和等于该产地的产量;中间 n个约束条件表示由各产地运往某一销地的商品 数量之和等于该销地的销量;最后nxm个约束条 件表示变量都是非负的 11
11 第一节 运输问题及其数学模型 在模型(3-2)式中,约束条件右侧常数ai和bj 满足(3-1)式。 在模型(3-2)中,目标函数表示运输总费用 极小化;前m个约束条件表示由某一产地运往各 个销地的商品数量之和等于该产地的产量;中间 n个约束条件表示由各产地运往某一销地的商品 数量之和等于该销地的销量;最后nm个约束条 件表示变量都是非负的

第一节运输问题及其数学模型 例1设有A1,A2,A是三座铁矿,每天要把 生产的铁矿石运往四个炼铁厂:B、B2、B,和B4。 各矿的产量、各厂的销量(百吨/天)以及各厂矿 间的运价(百元/百吨)如表3-2所示。问应如何 组织调运才能使总运费最少? 12
12 第一节 运输问题及其数学模型 例1 设有A1,A2,A3是三座铁矿,每天要把 生产的铁矿石运往四个炼铁厂:Bl、B2、B3和B4。 各矿的产量、各厂的销量(百吨/天)以及各厂矿 间的运价(百元/百吨)如表3-2所示。问应如何 组织调运才能使总运费最少?