
(-1y=-(-1, 故D=-∑(1少4n,0p,.am.0. =-D证毕 例如 17 5 17 5 17 5 715 2=-3 5 1←→C2 6 6 8 66 2 三一 6 6 2. 3 5 8 6 62 35 8 5 3 8 推论 如果行列式有两行(列)完全相同,则 此行列式为零 证明互换相同的两行,有D=一D, .D=0
例如 推论 如果行列式有两行(列)完全相同,则 此行列式为零. 证明 互换相同的两行,有 D = 0. D = −D, ( 1) ( 1) , 1 t t − = − − 故 ( 1) . 1 1 D1 a1 a a a D j i npn p ip jp t = − − = − 证毕 , 1 7 5 1 7 5 6 6 2 = − 3 5 8 . 8 2 5 8 2 5 = − 3 6 1 5 6 7 5 6 7 3 6 1 6 6 2 3 5 8 2 3 r r 1 2 c c

性质3行列式的某一行(列) 中所有的元素都 乘以同一数k,等于用数k乘此行列式 11 L12 11 L12 n kai kai2 kain =k ai Qi2 Qin nn 第i行(或列)乘以k,记作r×k(或C,×k) 推论行列式的某一行(列)中所有元素的公因 子可以提到行列式符号的外面. 第行(或列)提出公因子k,记作÷k(或C,÷k)
性质3 行列式的某一行(列)中所有的元素都 乘以同一数 k ,等于用数 k 乘此行列式. n n nn i i in n a a a ka ka ka a a a 1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a k 1 2 1 2 11 12 1 = 推论 行列式的某一行(列)中所有元素的公因 子可以提到行列式符号的外面. 第i行(或列)乘以k,记作 r k( c k). i 或 i 第i行(或列)提出公因子k,记作 r k( c k). i 或 i
举例说明性质3及其推论 2 23 23 0 -1 -1 4 二0 -1 1 2 -3 4 -3 -3 4 8 -12 16 (一个数 对列也有相同的运算,同学们可以试一试。 实际计算时常用推论的形式,比如 1 2 3 ”÷4 2 3 0 0 -1 8 -1216 2 -3 第三行有公因子4
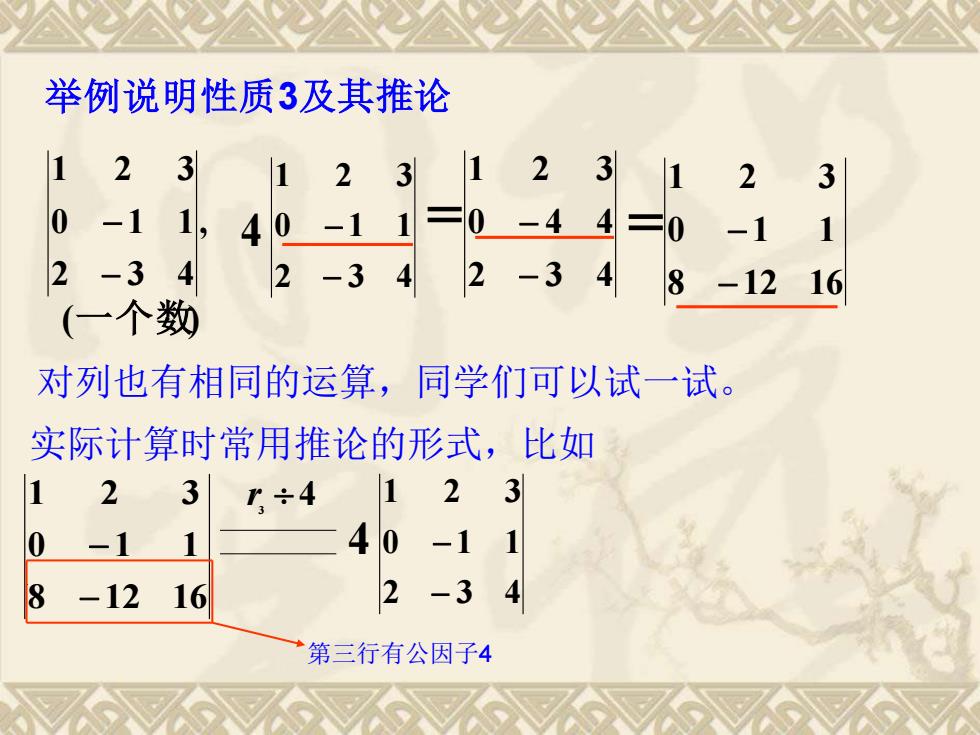
举例说明性质3及其推论 , 2 3 4 0 1 1 1 2 3 − − (一个数) 2 3 4 0 1 1 1 2 3 − 4 − = = 2 3 4 0 4 4 1 2 3 − − 8 12 16 0 1 1 1 2 3 − − 对列也有相同的运算,同学们可以试一试。 实际计算时常用推论的形式,比如 8 12 16 0 1 1 1 2 3 − − r 3 4 4 2 3 4 0 1 1 1 2 3 − − 第三行有公因子4

性质4 行列式中如果有两行(列)元素成比 例,则此行列式为零. 证明 11 L12 n 12 。 n 1 ai2 迎 u Ai2 。· in K =0. kai kai2 KQin ai Ai2 in An2 (nl (n2 a nn
性质4 行列式中如果有两行(列)元素成比 例,则此行列式为零. 证明 n n nn i i in i i in n a a a ka ka ka a a a a a a 1 2 1 2 1 2 11 12 1 n n nn i i in i i in n a a a a a a a a a a a a k 1 2 1 2 1 2 11 12 1 = = 0

性质5 若行列式的某一列(行)的元素都是两 数之和. 11 L12 ·. (av ali) in 例如 D 021 L22 (azi+azi) An2 (ani+a) (nn 则D等于下列两个行列式之和: 11 Avi .1n L11 .n D= L21 Azi .·l2n L21 d .l2n ni i .Qnn
性质5 若行列式的某一列(行)的元素都是两 数之和. n n ni ni nn i i n i i n a a a a a a a a a a a a a a a D ( ) ( ) ( ) 1 2 2 1 2 2 2 2 2 1 1 1 2 1 1 1 + + + = 则D等于下列两个行列式之和: n ni nn i n i n n ni nn i n i n a a a a a a a a a a a a a a a a a a D = + 1 2 1 2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 例如