and(6)Portland,Oregon。凭直觉,货栈是过多了,就是说,在不会过多的增加运输成本和服 务成本的前提下,可以考虑关闭一些货栈来减少一定数量的固定成本。相关数据是按月采集 的,详见下面的表格: 成本矩阵(每吨-月) 需求城市 月供应 能力 月固定 货栈 2 3 5 6 (吨) 成本 A $1675 $400 $685 $1630 $1160 $2800 18 $7,650 B 1460 1940 970 100 495 1200 24 3,500 c 1925 2400 1425 500 950 800 27 3,500 D 380 1355 543 1045 665 2321 22 4.100 E 922 1646 700 508 311 1797 31 2.200 每月需求量 10 8 12 6 7 11 (吨) 表6-1Zyx公司销售数据 例如,关闭货栈A(Baltimore)每月将节约固定成本$7,650。如果城市5(Omaha)从E (Wichita)获得它的全部需求,则每月供应给城市Omaha的运输成本是7×31l=$2,177。并 不要求一个消费者一定从唯一的城市或得全部需求。这样的多来源是因为一个货栈只具备有 限的供应能力(例如,Cheyenn每月只能提供24吨)。Zyzx打算关掉一个货栈,它将关闭那 一个呢? 我们用2种不同的方法来求解或近似地求解这个问题: 1)逐步增加的方式:一开始没有一个工厂开工,然后增加成本减少幅度最大的工 厂,.,直到再增加工厂也无利可图为止。 2)逐步减少的方式:一开始所有的工厂都开工,然后减少成本节约幅度最大的工 厂,.,直到再减少工厂也无利可图为止。 试探式3和4的有利之处是应用起来比较方便。下面是用2种方法计算出来的结果: 方法 最优目标值时间(秒) 开工的工厂目标函数值 松P 46,031 3.38 A,B,D 35,662 紧P 46,031 1.67 A,B,D 46,031 逐步增加方式 46.943 nil A,B,D,E
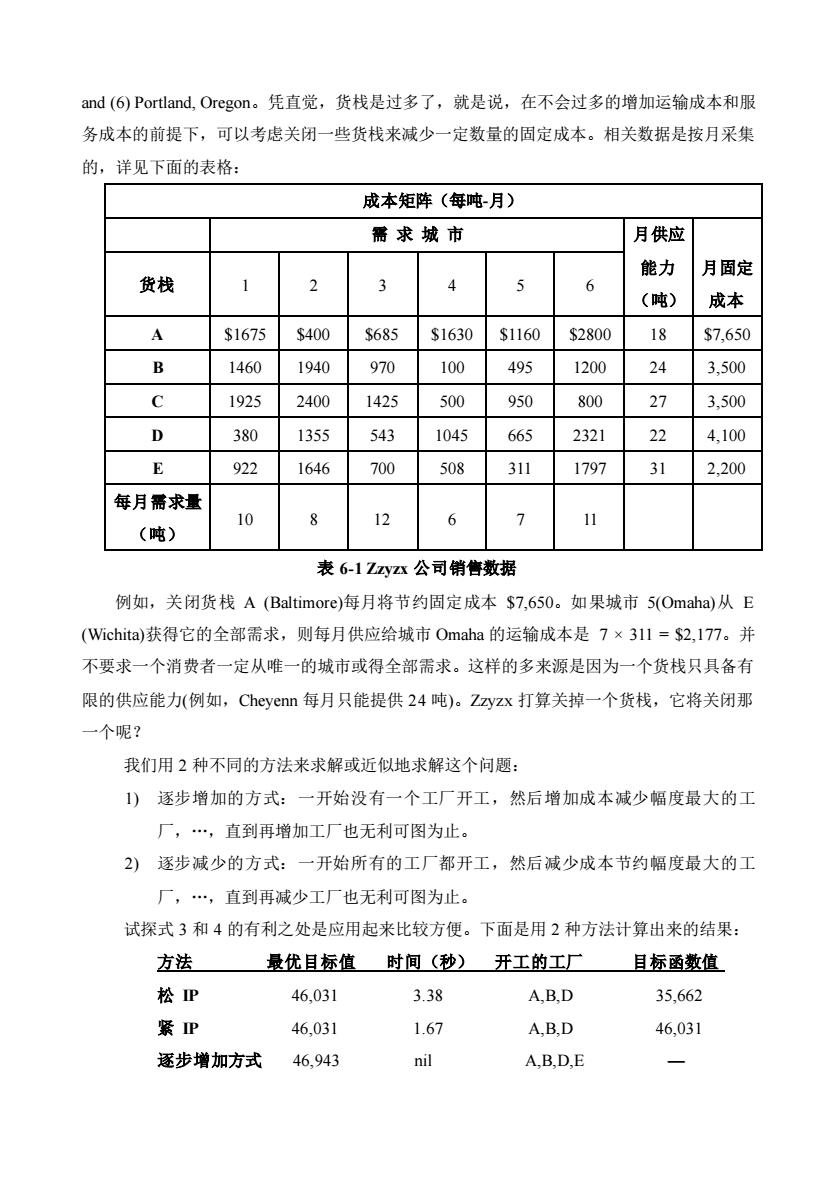
and (6) Portland, Oregon。凭直觉,货栈是过多了,就是说,在不会过多的增加运输成本和服 务成本的前提下,可以考虑关闭一些货栈来减少一定数量的固定成本。相关数据是按月采集 的,详见下面的表格: 成本矩阵(每吨-月) 需 求 城 市 月供应 能力 (吨) 月固定 成本 货栈 1 2 3 4 5 6 A $1675 $400 $685 $1630 $1160 $2800 18 $7,650 B 1460 1940 970 100 495 1200 24 3,500 C 1925 2400 1425 500 950 800 27 3,500 D 380 1355 543 1045 665 2321 22 4,100 E 922 1646 700 508 311 1797 31 2,200 每月需求量 (吨) 10 8 12 6 7 11 表 6-1 Zzyzx 公司销售数据 例如,关闭货栈 A (Baltimore)每月将节约固定成本 $7,650。如果城市 5(Omaha)从 E (Wichita)获得它的全部需求,则每月供应给城市 Omaha 的运输成本是 7 × 311 = $2,177。并 不要求一个消费者一定从唯一的城市或得全部需求。这样的多来源是因为一个货栈只具备有 限的供应能力(例如,Cheyenn 每月只能提供 24 吨)。Zzyzx 打算关掉一个货栈,它将关闭那 一个呢? 我们用 2 种不同的方法来求解或近似地求解这个问题: 1) 逐步增加的方式:一开始没有一个工厂开工,然后增加成本减少幅度最大的工 厂,.,直到再增加工厂也无利可图为止。 2) 逐步减少的方式:一开始所有的工厂都开工,然后减少成本节约幅度最大的工 厂,.,直到再减少工厂也无利可图为止。 试探式 3 和 4 的有利之处是应用起来比较方便。下面是用 2 种方法计算出来的结果: 方法 最优目标值 时间(秒) 开工的工厂 目标函数值 松 IP 46,031 3.38 A,B,D 35,662 紧 IP 46,031 1.67 A,B,D 46,031 逐步增加方式 46,943 nil A,B,D,E —

逐步减少方式46,443 nil A,C,D,E 注意,尽管松P模型与紧P模型的最优解相等,但是,前者所用的计算时间是后者的 两倍。对于一个大型问题,这种差别将更加显著。对于紧P模型,相应的LP模型(去掉整 数变量的约束)的目标函数值与紧P模型的最优目标函数值相等。所以,紧P模型被当作 LP模型来求解的时候,得到的解答自然是整数。 单一产品的动态批量规模问题可以描述如下: n=一个产品计划生产的周期数: D=j周期预计的需求数量,j=1,2,.,n 6=产品在周期i生产的固定成本: h,=在周期i的单位产品库存到周期i+1的成本。 这个问题可以看成是一个简单工厂定位问题。我们定义: c=D,∑h 就是说,c时是用周期i的产品供应j期需求的成本。每个周期可以看成是一个工厂工地 和一个消费者。 更进一步,如果周期ⅰ只有有限的生产能力K,这时,能力受限的动态批量规模问题就 是一个特殊的能力受限制的工厂定位问题。 6.2.7表示具有一般阶梯状的成本曲线 在工厂定位问题中固定成本加线性变动成本曲线便是更加一般的阶梯状成本曲线(见下 面的图6-2)的一个特例。 三段斜率分别是C1,c2和c3。截距K2和K3是由公式K+1=K+CU:-c+1U确定。如果 C+1<C,则是一个具有规模效益经济活动的成本曲线。如果我们从一个供货商处购买商品时, 有数量规模折扣,就会有类似的成本曲线
逐步减少方式 46,443 nil A,C,D,E — 注意,尽管松 IP 模型与紧 IP 模型的最优解相等,但是,前者所用的计算时间是后者的 两倍。对于一个大型问题,这种差别将更加显著。对于紧 IP 模型,相应的 LP 模型(去掉整 数变量的约束)的目标函数值与紧 IP 模型的最优目标函数值相等。所以,紧 IP 模型被当作 LP 模型来求解的时候,得到的解答自然是整数。 单一产品的动态批量规模问题可以描述如下: n = 一个产品计划生产的周期数; Dj = j 周期预计的需求数量,j = 1, 2,.,n; fi = 产品在周期 i 生产的固定成本; hi = 在周期 i 的单位产品库存到周期 i + 1 的成本。 这个问题可以看成是一个简单工厂定位问题。我们定义: cij = − = 1 1 j i Dj hi 就是说,cij 是用周期 i 的产品供应 j 期需求的成本。每个周期可以看成是一个工厂工地 和一个消费者。 更进一步,如果周期 i 只有有限的生产能力 Ki,这时,能力受限的动态批量规模问题就 是一个特殊的能力受限制的工厂定位问题。 6.2.7 表示具有一般阶梯状的成本曲线 在工厂定位问题中固定成本加线性变动成本曲线便是更加一般的阶梯状成本曲线(见下 面的图 6-2)的一个特例。 三段斜率分别是 c1, c2 和 c3。截距 K2 和 K3 是由公式 Ki+1 = Ki + ciUi - ci+1 Ui 确定。如果 ci+1 < ci, 则是一个具有规模效益经济活动的成本曲线。如果我们从一个供货商处购买商品时, 有数量规模折扣,就会有类似的成本曲线

案K K 60 U x 图6-2凹面分段线性成本曲线 表示这样的成本曲线有好几种方法。第1种方法就是前面表示一个固定成本加线性变动 成本曲线方法的推广。如果整个模型只有少数这样的曲线,而每个曲线只有一、两个转折点, 这个方法还是比较满意的。 定义: y=1如果U-1≤x<U,否则0 (a) x=X如果U1≤x<Ui,否则0 (b) 相应的模型应该包含下面的项目: MN=K*y1+K2*y2+K3*y3+C1*X1+C2*X2+C3*X3+.: 如果x在模型的其它地方出现,就可以用x1+发+x3取代。如果是01变量,那么上 面的约束确实正确表达了成本函数。如果成本曲线是凹面且关于ⅹ没有上限,那么约束集合 (b)就没有必要了。 6.2.8实例2 假设在一个大型问题中要确定向一个供货商订货(有数量折扣)的问题。情况是这样的: 一次订货的固定成本是$150。最初1,000加仑的产品每加仑价格是$2。超过1,000加仑的部 分每加仑的价格下降到$1.90。我们最多只能购买5,000加仑的产品。问题的各种参数计算如 下: K1=150: U1=1,000: K2=150+1,000×2-1,000×1.90=250: U2=5,000:
图 6-2 凹面分段线性成本曲线 表示这样的成本曲线有好几种方法。第 1 种方法就是前面表示一个固定成本加线性变动 成本曲线方法的推广。如果整个模型只有少数这样的曲线,而每个曲线只有一、两个转折点, 这个方法还是比较满意的。. 定义: yi =1 如果 Ui-1 ≤ x < Ui, 否则 0 (a) xi = x 如果 Ui-1 ≤ x < Ui, 否则 0 (b) 相应的模型应该包含下面的项目: MIN = Kl*y1 + K2*y2 + K3*y3 + C1*X1 + C2*X2 + C3*X3 +.; 如果 x 在模型的其它地方出现,就可以用 x1 + x2 + x3 取代。如果 yi 是 0/1 变量,那么上 面的约束确实正确表达了成本函数。如果成本曲线是凹面且关于 x 没有上限,那么约束集合 (b)就没有必要了。 6.2.8 实例 2 假设在一个大型问题中要确定向一个供货商订货(有数量折扣)的问题。情况是这样的: 一次订货的固定成本是$150。最初 1,000 加仑的产品每加仑价格是$2。超过 1,000 加仑的部 分每加仑的价格下降到$1.90。我们最多只能购买 5,000 加仑的产品。问题的各种参数计算如 下: K1 = 150; U1 = 1,000; K2 = 150 + 1,000 × 2 - 1,000 × 1.90 = 250; U2 = 5,000;
定义变量: y1=1如果购买的数量大于0且不超过1,000,否则0: y2=1如果购买的数量大于1,000,否则0: x1=购买的加仑数量,如果购买的数量不超过1,000: X2=购买的加仑数量,如果购买的数量超过1,000。 相应的模型一定包括: MIN=150*y1*250*y2+2*x1+1.9*x2+.; !s.t.; x1 <=1000 *y1; x2 <=5000 *y2; y1+ y2 <=1; @BIN(y1);eBIN(y1);.·· !限制变量y是整数变量: 6.2.9非线性成本曲线的选择性表示 下面我们用一个选择性表示方法来表示下面图6-3中的成本曲线。 K3 成K2 0 Ui X U2 U3 图6-3任意分段线性成本曲线 假设函数在断点X=U,x=U+1之间是线性函数(=1,2,.)。函数在第i个断点的函数 值用v:(i.e.,v=f(U)表示。 这样一个具有个断点的函数可以用一个线性规划表示
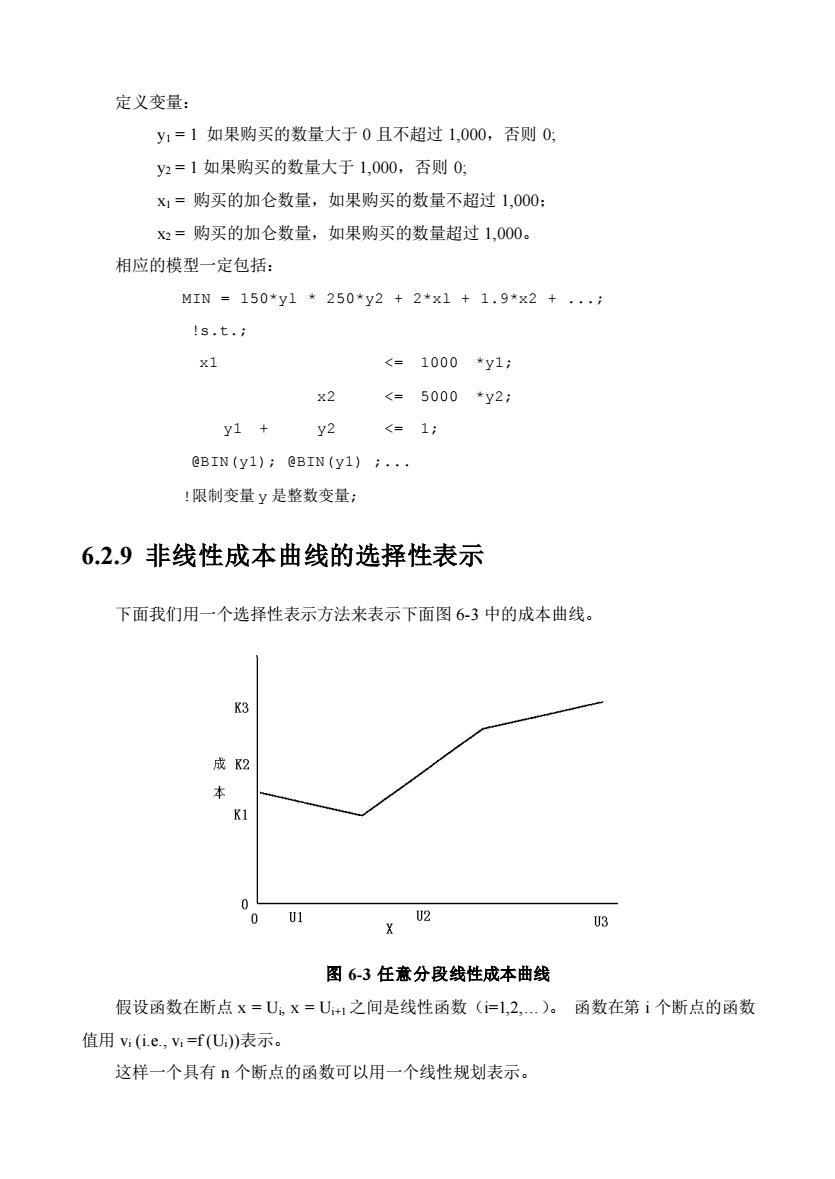
定义变量: y1 = 1 如果购买的数量大于 0 且不超过 1,000,否则 0; y2 = 1 如果购买的数量大于 1,000,否则 0; x1 = 购买的加仑数量,如果购买的数量不超过 1,000; x2 = 购买的加仑数量,如果购买的数量超过 1,000。 相应的模型一定包括: MIN = 150*yl * 250*y2 + 2*xl + 1.9*x2 + .; !s.t.; x1 <= 1000 *y1; x2 <= 5000 *y2; y1 + y2 <= 1; @BIN(y1); @BIN(y1) ;. !限制变量 y 是整数变量; 6.2.9 非线性成本曲线的选择性表示 下面我们用一个选择性表示方法来表示下面图 6-3 中的成本曲线。 图 6-3 任意分段线性成本曲线 假设函数在断点 x = Ui, x = Ui+1 之间是线性函数(i=1,2,.)。 函数在第 i 个断点的函数 值用 vi (i.e., vi =f (Ui))表示。 这样一个具有 n 个断点的函数可以用一个线性规划表示

1)增加约束:w1+w2+.+wa=1 2)用下面的表达式替换任何一个x的值: WIU1+W2U2++WnUn 3)用下面的表达式替换任何一个(x)的值: W1V1+W2V2++WnVn 4)最多只允许有两个不等于0且相邻w的值,其它的值都是0。 新变量w指定了点U的权数。如果函数f(x)在两个相邻的点X=U:和x=UH之间 是线性函数,x=wU+w+1U+1满足w+w+1=1,那么,fx)=wU)+W+1fU+1)=wV+ Wi+l Vi+lo 可以用数种方法形成约束(4)。约束(1)可以用一些P代码表示,就是所谓的“第2类特 殊命令集合”或简称“SOS2”。对于用$OS2表示的每一个约束将自动满足约束(4)。 如果我们有一个标准的P代码,而没有SOS2特征,那么约束(4)可以用下面一系列约束 表示: WI ≤z1 W2 ≤Z1+Z2 W3≤Z2+Z3 wn-1≤Zn-2+Zn-l Wn ≤zn-1 Z1+Z2+.+Zn-=1 Zi=0or 1. 总结如下,处理一个非线性项目需要一个约束和n个变量。如果没有SOS2特征,处理 一个非线性项目必须增加n个约束和n-1个变量。 这里描述的一般方法有时称为拉姆达方法。 6.2.10将乘积函数转换成分离函数 前面介绍的方法只能是用来处理一个变量的非线性函数。还有一些标准的方法可以用来 转换一个多变量函数,所以,一个函数也可以利用转换变量用分离的形式表示。最普通的转
1) 增加约束:w1+ w2 +. + wn = 1 2) 用下面的表达式替换任何一个 x 的值: w1U1+ w2U2+.+ wnUn 3) 用下面的表达式替换任何一个 f(x)的值: w1v1+ w2v2+.+ wnvn 4) 最多只允许有两个不等于 0 且相邻 wi 的值,其它的值都是 0。 新变量 wi 指定了点 Ui 的权数。如果函数 f(x)在两个 相邻的点 x = Ui 和 x = Ui+l 之间 是线性函数,x = wiUi+ wi+1Ui+1 满足 wi + wi.+1 = 1,那么,f(x) = wif(Ui) + wi+1f(Ui+1 ) = wivi+ wi+1vi+1。 可以用数种方法形成约束(4)。约束(1)可以用一些 IP 代码表示,就是所谓的“第 2 类特 殊命令集合”或简称“SOS2”。对于用 SOS2 表示的每一个约束将自动满足约束(4)。 如果我们有一个标准的 IP 代码,而没有 SOS2 特征,那么约束(4)可以用下面一系列约束 表示: w1 ≤ z1 w2 ≤ z1 + z2 w3 ≤ z2 + z3 . . . wn-1 ≤ zn-2 + zn-1 wn ≤ zn- 1 z1 + z2 + . + zn-l = 1 zi = 0 or 1. 总结如下,处理一个非线性项目需要一个约束和 n 个变量。如果没有 SOS2 特征,处理 一个非线性项目必须增加 n 个约束和 n – 1 个变量。 这里描述的一般方法有时称为拉姆达方法。 6.2.10 将乘积函数转换成分离函数 前面介绍的方法只能是用来处理一个变量的非线性函数。还有一些标准的方法可以用来 转换一个多变量函数,所以,一个函数也可以利用转换变量用分离的形式表示。最普通的转