《运筹学》课程教学资源（参考资料）5 物料调和模型

5物料调和模型 5.1引言 在物料调和问题中，通常有： 1)两种或多种原材料： 2)一个或多个质量指标（对于每一种原材料）； 3)一种或多种产品（通过调和原材料生产出），并使得产品的质量达到一定的要 求。 计算产品质量指标的一种理想方法就是对原材料的质量指标进行加权平均而获得。 下面是一些实例： 产品 质量 原材料 饲料 水分，浓度，进口原料含量，有害成分 各类原始饲料 食物 蛋白质，碳水化合物，脂肪含量 玉米，燕麦，大豆，肉类 汽油 辛烷值，挥发性，蒸汽压 提炼的各类原油产品 粗粉 碳，锰，铬的含量 粗粉矿石，金属碎片 出口的粮食水分，进口原料和有害成分的百分比各类粮食供应商 销售的煤炭硫磺，热量，灰分，水分含量 伊利诺斯州，怀俄明州煤炭 酒 年限，种类，地域 各地的纯生酒 银行资产 平衡表 各类贷款比例贷款期限投资利率 可能的各类贷款和投资 在下面的三种工业中经常使用调和模型： 1)饲料和食品工业（例如，调和牛饲料，热狗等等）： 2)金属加工业（例如，调和特种钢和特种合金，尤其是在再生废料的使用中）： 3)石油工业（例如，调和指定辛烷值和蒸汽压的汽油）。 某类原材料的市场价格在一个月或一个星期内也许会发生较大的变化。例如，明智的 采购员会从最便宜的供应商那里采购玉米。更为聪明的采购员会利用这样的事实：当玉米 的价格相对于大豆有所下降时，用同样多的钱，多采购玉米，少采购大豆就会得到更好的 经济效果。 美国科学家菲尔德在1978年为饲养场的家畜构造了一个低成本的饲料调和模型。饲 养场的管理员每月要运行1000次模型。艾伦在1998年对美国韦尔奇有限公司的葡萄汁调 和问题进行了研究。调和葡萄汁涉及的质量指标是甜度、酸度和色泽。这样的调和问题每 一个季度至少要做一次，要决定从韦尔奇的供应商那里购进什么种类的葡萄及其数量。长 期的供货合同迫使韦尔奇收购每一个供应商的全部产品。 近一段时间以来，在钢铁业的小工厂中有一些成功的例子。这些小工厂多数都是使用 回收的废钢铁进行再加工。相应的调和问题就是：使用何种废料，数量是多少，才能达到

1 5 物料调和模型 5.1 引言 在物料调和问题中，通常有: 1） 两种或多种原材料; 2） 一个或多个质量指标（对于每一种原材料）; 3） 一种或多种产品（通过调和原材料生产出），并使得产品的质量达到一定的要 求。 计算产品质量指标的一种理想方法就是对原材料的质量指标进行加权平均而获得。 下面是一些实例: 产品 质量 原材料 饲料 水分, 浓度, 进口原料含量，有害成分 各类原始饲料 食物 蛋白质, 碳水化合物, 脂肪含量 玉米, 燕麦, 大豆, 肉类 汽油 辛烷值, 挥发性, 蒸汽压 提炼的各类原油产品 粗粉 碳, 锰, 铬的含量 粗粉矿石, 金属碎片 出口的粮食 水分, 进口原料和有害成分的百分比 各类粮食供应商 销售的煤炭 硫磺, 热量, 灰分, 水分含量 伊利诺斯州, 怀俄明州煤炭 酒 年限, 种类, 地域 各地的纯生酒 银行资产 平衡表 各类贷款比例 贷款期限 投资利率 可能的各类贷款和投资 在下面的三种工业中经常使用调和模型： 1) 饲料和食品工业 (例如，调和牛饲料，热狗等等); 2） 金属加工业 (例如，调和特种钢和特种合金，尤其是在再生废料的使用中); 3） 石油工业 (例如，调和指定辛烷值和蒸汽压的汽油)。 某类原材料的市场价格在一个月或一个星期内也许会发生较大的变化。例如，明智的 采购员会从最便宜的供应商那里采购玉米。更为聪明的采购员会利用这样的事实：当玉米 的价格相对于大豆有所下降时，用同样多的钱，多采购玉米，少采购大豆就会得到更好的 经济效果。 美国科学家菲尔德在 1978 年为饲养场的家畜构造了一个低成本的饲料调和模型。饲 养场的管理员每月要运行 1000 次模型。艾伦在 1998 年对美国韦尔奇有限公司的葡萄汁调 和问题进行了研究。调和葡萄汁涉及的质量指标是甜度、酸度和色泽。这样的调和问题每 一个季度至少要做一次，要决定从韦尔奇的供应商那里购进什么种类的葡萄及其数量。长 期的供货合同迫使韦尔奇收购每一个供应商的全部产品。 近一段时间以来，在钢铁业的小工厂中有一些成功的例子。这些小工厂多数都是使用 回收的废钢铁进行再加工。相应的调和问题就是：使用何种废料，数量是多少，才能达到

2 产品（例如，承重棒等等）的质量要求？ 第一个公开发表的LP模型就是一个调和或营养问题，是由George Stigler在1945年 完成。这个问题需要从80中食品中构造一个“处方”，使得调和的产品满足12种营养的 需求。例如，蛋白质要超过5%，纤维素要超过40%等等。当Stigler给出这个模型的时候， 还没有出现求解LP的单纯形算法。因此，人们还没有意识到这个“营养问题”恰好就是 这类调和问题的一个特例。Stigler意识到了它的一般性，他说“到目前为止，还没有任何 直接的方法可以解决线性约束下线性函数的最小值问题”。对于这个特殊的问题，他借助 于参数变换给出的解答与后来用单纯形法计算的最低成本解答只有几分币的差距。无论是 最低成本解答还是Stigler的解答，从烹饪的角度来看都是不可行的。试想一下，人们能够 将由卷心菜、面粉和干青豆一起吞下吗？我们不清楚，是有人需要这样的食品，还是有人 可以忍受这样的食品？从这些解答中，我们可以看出约束的重要性。有些约束虽然是显而 易见的，但也常常会被遗忘。在这个例子中，被遗忘的约束是可口性约束。 5.2调和问题的结构和实例 5.2.1调和问题的结构 让我们来考察一个简单的食品调和问题。我们要生产一种牲畜饲料，其蛋白质含量至少 超过15%。使用的原材料是玉米（蛋白质含量6%）和大豆（蛋白质含量35%）。 关于蛋白质的约束如下： 调和物中蛋白质（蒲式尔） ≥0.15 调和物（蒲式尔） 如果C表示调和物中玉米的数量（蒲式尔），S表示调和物中大豆的数量，那么，我 们有 0.06C+0.35S ≥0.15 C+S 因为这个约束不是线性的，初看起来，似乎有点麻烦。当然，如果将不等式两边同乘 (C+S),就可以得到下面等价的约束： 0.06C+0.35S≥0.15(C+S) 再将它标准化，得到 -0.09C+0.20S≥0 对于其它指标的约束（例如，脂肪，碳水化合物、色泽、味道和质地等）都可以按照 类似的方法处理。 调和问题的一个最大的特点是当直接给出约束的时候，关键约束是以线性比率的形式 出现。当然，可以通过同乘分母将它们转化成线性约束。在一些金融模型中也会出现比率 约束。金融机构关于投放贷款比例的约束或投资周期的约束就是比率约束。 如果在一个大的问题中，当批量也是决策变量，而调和因素只是占很小的比率时，相

2 产品（例如，承重棒等等）的质量要求？ 第一个公开发表的 LP 模型就是一个调和或营养问题，是由 George Stigler 在 1945 年 完成。这个问题需要从 80 中食品中构造一个“处方”，使得调和的产品满足 12 种营养的 需求。例如，蛋白质要超过 5%，纤维素要超过 40%等等。当 Stigler 给出这个模型的时候， 还没有出现求解 LP 的单纯形算法。因此，人们还没有意识到这个“营养问题”恰好就是 这类调和问题的一个特例。Stigler 意识到了它的一般性，他说“到目前为止，还没有任何 直接的方法可以解决线性约束下线性函数的最小值问题”。对于这个特殊的问题，他借助 于参数变换给出的解答与后来用单纯形法计算的最低成本解答只有几分币的差距。无论是 最低成本解答还是 Stigler 的解答，从烹饪的角度来看都是不可行的。试想一下，人们能够 将由卷心菜、面粉和干青豆一起吞下吗？我们不清楚，是有人需要这样的食品，还是有人 可以忍受这样的食品？从这些解答中，我们可以看出约束的重要性。有些约束虽然是显而 易见的，但也常常会被遗忘。在这个例子中，被遗忘的约束是可口性约束。 5.2 调和问题的结构和实例 5.2.1 调和问题的结构 让我们来考察一个简单的食品调和问题。我们要生产一种牲畜饲料,其蛋白质含量至少 超过 15%。使用的原材料是玉米（蛋白质含量 6%）和大豆（蛋白质含量 35%）。 关于蛋白质的约束如下：  0.15 调和物（蒲式尔） 调和物中蛋白质（蒲式尔） 如果 C 表示调和物中玉米的数量（ 蒲式尔 ），S 表示调和物中大豆的数量，那么，我 们有 0.15 C S 0.06 C 0.35S  + + 因为这个约束不是线性的，初看起来，似乎有点麻烦。当然，如果将不等式两边同乘 (C+S)，就可以得到下面等价的约束： 0.06 C + 0.35 S ≥ 0.15 (C+S) 再将它标准化，得到 - 0.09 C + 0.20 S ≥ 0 对于其它指标的约束（例如，脂肪，碳水化合物、色泽、味道和质地等）都可以按照 类似的方法处理。 调和问题的一个最大的特点是当直接给出约束的时候，关键约束是以线性比率的形式 出现。当然，可以通过同乘分母将它们转化成线性约束。在一些金融模型中也会出现比率 约束。金融机构关于投放贷款比例的约束或投资周期的约束就是比率约束。 如果在一个大的问题中，当批量也是决策变量，而调和因素只是占很小的比率时，相

3 应的模型就要复杂一点。 5.2.2实例：匹斯堡钢铁公司的调和问题 匹斯堡钢铁公司(PS)计划生产一种新型的高碳钢，其质量要求如下： 至少 至多 碳含量 3.00% 3.50% 铬含量 0.30% 0.45% 锰含量 0.35% 1.65% 硅含量 2.70% 3.00% PS可以利用以下的原材料： 成本（磅）碳（%)铬（%) 锰（%)硅(%) 可用量 铸铁1 0.0300 4.0 0.0 0.9 2.25 无限制 铸铁2 0.0645 0.0 10.0 4.5 15.00 无限制 铁硅1 0.0650 0.0 0.0 0.0 45.00 无限制 铁硅2 0.0610 0.0 0.0 0.0 42.00 无限制 合金1 0.1000 0.0 0.0 60.0 18.00 无限制 合金2 0.1300 0.0 20.0 9.0 30.00 无限制 合金3 0.1190 0.0 8.0 33.0 25.00 无限制 碳化物（硅） 0.0800 15.0 0.0 0.0 30.00 20磅 钢锭1 0.0210 0.4 0.0 0.9 0.00 200磅 钢锭2 0.0200 0.1 0.0 0.3 0.00 200磅 钢锭3 0.0195 0.1 0.0 0.3 0.00 200磅 根据合同，需要生产一吨(2000-磅)高碳钢。现在的问题是：选择哪些原材料进行调 和，每一种原材料的数量应该是多少，才能达到即满足质量的要求，又能使得总成本最少 的目的？有经验的炼钢工人估计：最低成本的治炼方式使用的原材料不会超过9种。最好 的调和方式是什么？很多原材料的价格和4种质量指标可以进行适当的调整。那些价格和 质量指标值得去调整。 注意，调和物中某种成分的含量可以用原材料相应成分的含量加权平均简单算出。例 如，如果合金1和合金2锰的含量分别是40%和60%，那么，调和物中，锰的含量就是： (0.40)×60+(0.60)×9=29.4。 5.2.3匹斯堡钢铁公司调和问题的模型和解答 PS调和问题的LP模型有11个变量和13个约束。11个变量是来自11种原材料。质 量指标中4种元素的上限构成了4个约束，4个下限也构成了4个约束。其它4个约束是 原材料用量上限的约束。最后一个是产品必须是2000磅的约束。 如果我们假设P1表示铸铁1的重量，对其它的原材料也做类似的处理。那么，就得 到成本最小化的模型： MODEL:

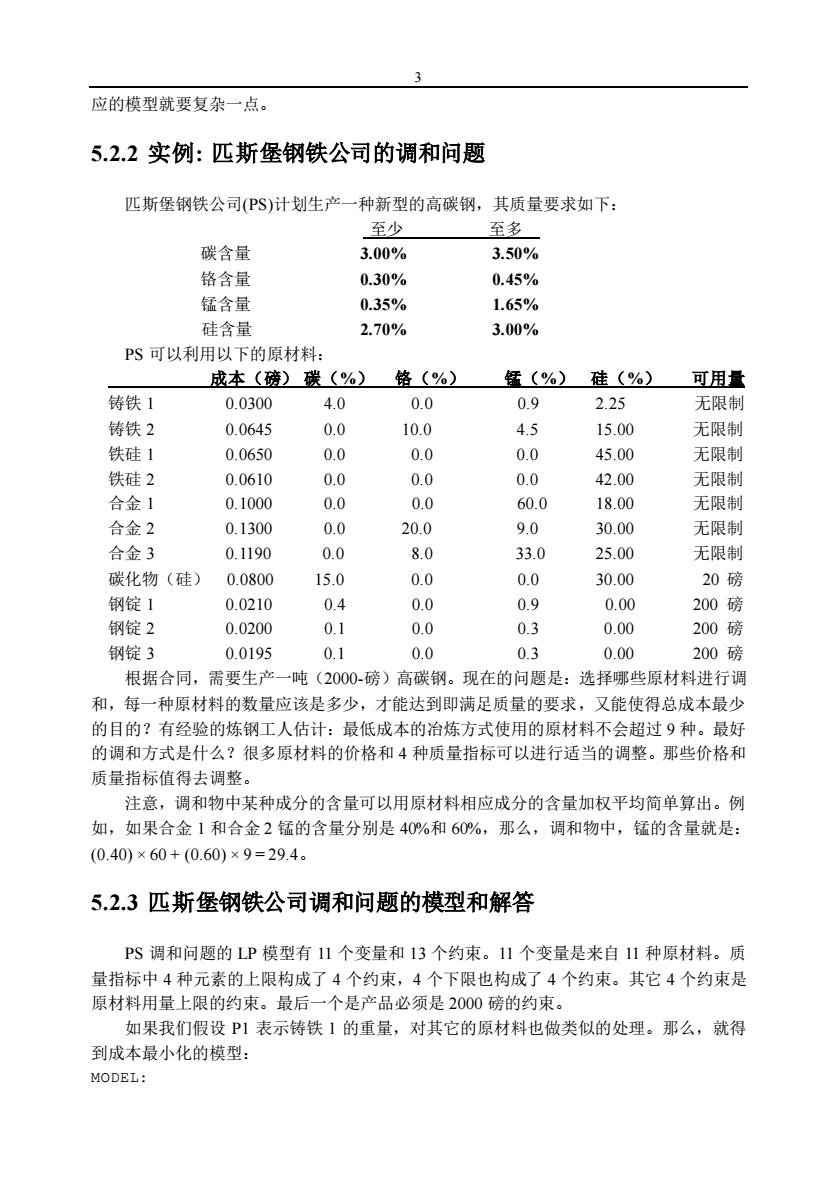
3 应的模型就要复杂一点。 5.2.2 实例: 匹斯堡钢铁公司的调和问题 匹斯堡钢铁公司(PS)计划生产一种新型的高碳钢，其质量要求如下： 至少 至多 碳含量 3.00% 3.50% 铬含量 0.30% 0.45% 锰含量 0.35% 1.65% 硅含量 2.70% 3.00% PS 可以利用以下的原材料： 成本（磅） 碳（%） 铬（%） 锰（%） 硅（%） 可用量 铸铁 1 0.0300 4.0 0.0 0.9 2.25 无限制 铸铁 2 0.0645 0.0 10.0 4.5 15.00 无限制 铁硅 1 0.0650 0.0 0.0 0.0 45.00 无限制 铁硅 2 0.0610 0.0 0.0 0.0 42.00 无限制 合金 1 0.1000 0.0 0.0 60.0 18.00 无限制 合金 2 0.1300 0.0 20.0 9.0 30.00 无限制 合金 3 0.1190 0.0 8.0 33.0 25.00 无限制 碳化物（硅） 0.0800 15.0 0.0 0.0 30.00 20 磅 钢锭 1 0.0210 0.4 0.0 0.9 0.00 200 磅 钢锭 2 0.0200 0.1 0.0 0.3 0.00 200 磅 钢锭 3 0.0195 0.1 0.0 0.3 0.00 200 磅 根据合同，需要生产一吨（2000-磅）高碳钢。现在的问题是：选择哪些原材料进行调 和，每一种原材料的数量应该是多少，才能达到即满足质量的要求，又能使得总成本最少 的目的？有经验的炼钢工人估计：最低成本的冶炼方式使用的原材料不会超过 9 种。最好 的调和方式是什么？很多原材料的价格和 4 种质量指标可以进行适当的调整。那些价格和 质量指标值得去调整。 注意，调和物中某种成分的含量可以用原材料相应成分的含量加权平均简单算出。例 如，如果合金 1 和合金 2 锰的含量分别是 40%和 60%，那么，调和物中，锰的含量就是： (0.40) × 60 + (0.60) × 9 = 29.4。 5.2.3 匹斯堡钢铁公司调和问题的模型和解答 PS 调和问题的 LP 模型有 11 个变量和 13 个约束。11 个变量是来自 11 种原材料。质 量指标中 4 种元素的上限构成了 4 个约束，4 个下限也构成了 4 个约束。其它 4 个约束是 原材料用量上限的约束。最后一个是产品必须是 2000 磅的约束。 如果我们假设 P1 表示铸铁 1 的重量，对其它的原材料也做类似的处理。那么，就得 到成本最小化的模型： MODEL:

MIN=0.03*P1+0.0645*P2+0.065*F1+0.061*F2+0.1*A1+0.13*A2+0.119*A3+0.08 *CB+0.021*S1+0.02*S2+0.0195*s3; !可以利用的原材料： CB<=20;S1<=200:S2<=200:S3<=200; ！质量要求： ！碳含量； 0.04*P1+0.15*CB+0.004*S1+0.001*S2+0.001*S3>=60: 0.04*P1+0.15*CB+0.004*S1+0.001*S2+0.001*S3<=70; ！铬含量： 0.1*P2+0.2*A2+0.08*A3>=6;10.003*2000=6: 0.1*P2+0.2*A2+0.08*A3<=9: ！锰含量； 0.009*P1+0.045*P2+0.6*A1+0.09*A2+0.33*A3+0.009*S1 +0.003*S2+0.003*s3>=27; 0.009*P1+0.045*P2+0.6*A1+0.09*A2+0.33*A3+0.009*S1 +0.003*S2+0.003*S3<=33; ！硅含量： 0.0225*P1+0.15*P2+0.45*F1+0.42*F2+0.18*A1+0.3*A2 +0.25*A3+0.3*CB>=54: 0.0225*P1+0.15*P2+0.45*F1+0.42*F2+0.18*A1+0.3*A2 +0.25*A3+0.3*CB<=60: Finish good requirements; !成品需求： P1+P2+F1+F2+A1+A2+A3+CB+S1+S2+S3=2000: END 简言之，这个模型就是 Minimize原材料成本 subject to (a)可利用的原材料 (b)质量需求 (c)成品需求 这种将约束归类的方法在实践中非常有用。 对于这个例子，当我们写质量约束的时候，可以利用产品重量为2000的性质将这些 约束进行适当的转化。例如，2000的3%就是60,2000的3.5%就是70，等等。 求解后，就可以得到下面的解答： Global optimal solution found at step: 10 Objective value: 59.55629 Variable Value Reduced Cost P1 1474.264 0.0000000 P2 60.00000 0.0000000

4 MIN=0.03*P1+0.0645*P2+0.065*F1+0.061*F2+0.1*A1+0.13*A2+0.119*A3+0.08 *CB+0.021*S1+0.02*S2+0.0195*S3; ! 可以利用的原材料; CB <= 20; S1 <= 200; S2 <= 200; S3 <= 200; ! 质量要求; ! 碳含量; 0.04 * P1 + 0.15 * CB + 0.004 * S1 + 0.001 * S2 + 0.001 * S3 >= 60; 0.04 * P1 + 0.15 * CB + 0.004 * S1 + 0.001 * S2 + 0.001 * S3 <= 70; ! 铬含量; 0.1 * P2 + 0.2 * A2 + 0.08 * A3 >= 6;!0.003*2000=6; 0.1 * P2 + 0.2 * A2 + 0.08 * A3 <= 9; ! 锰含量; 0.009 * P1 + 0.045 * P2 + 0.6 * A1 + 0.09 * A2 + 0.33 * A3 + 0.009 * S1 + 0.003 * S2 + 0.003 * S3 >= 27; 0.009 * P1 + 0.045 * P2 + 0.6 * A1 + 0.09 * A2 + 0.33 * A3 + 0.009 * S1 + 0.003 * S2 + 0.003 * S3 <= 33; ! 硅含量; 0.0225 * P1 + 0.15 * P2 + 0.45 * F1 + 0.42 * F2 + 0.18 * A1 + 0.3 * A2 + 0.25 * A3 + 0.3 * CB >= 54; 0.0225 * P1 + 0.15 * P2 + 0.45 * F1 + 0.42 * F2 + 0.18 * A1 + 0.3 * A2 + 0.25 * A3 + 0.3 * CB <= 60; ! Finish good requirements; !成品需求; P1 + P2 + F1 + F2 + A1 + A2 + A3 + CB + S1 + S2 + S3 = 2000; END 简言之，这个模型就是: Minimize 原材料成本 subject to (a) 可利用的原材料 (b) 质量需求 (c) 成品需求 这种将约束归类的方法在实践中非常有用。 对于这个例子，当我们写质量约束的时候，可以利用产品重量为 2000 的性质将这些 约束进行适当的转化。例如，2000 的 3% 就是 60，2000 的 3.5%就是 70，等等。 求解后，就可以得到下面的解答： Global optimal solution found at step: 10 Objective value: 59.55629 Variable Value Reduced Cost P1 1474.264 0.0000000 P2 60.00000 0.0000000

5 F1 0.0000000 0.1035937E-02 F2 22.06205 0.0000000 A1 14.23886 0.0000000 A2 0.0000000 0.2050311E-01 A3 0.0000000 0.1992597E-01 CB 0.0000000 0.3356920E-02 s1 200.0000 0.0000000 S2 29.43496 0.0000000 s3 200.0000 0.0000000 注意，调和后的产品仅仅利用了7种原材料。 在实践中，匹斯堡公司基本上每月要运行两次。第一次运行结束后，采购商根据递减 成本和影子价格来指导购买原材料。第二次运行结束后，制造商就会从生产的产品中获得 收益。 5.3案例及参考解答 5-1.这个星期，Exxoff公司必须对合成汽油产品作出决定。他们要合成两种汽油产品， 产品的特性列表如下： 汽油产品 蒸汽压 辛烷数 售价S桶 Lo-lead <=7 >=80 $9.80 Premium <=6 >=100 $12.00 构成两种汽油的原料及它们的特性列表如下： 原料 蒸汽压 辛烷数 本周可供量（桶） Cat-Cracked Gas 8 83 2700 Isopentane 20 109 1350 Straight Gas 4 74 4100 汽油产品中的蒸汽压和辛烷数可简单地按照它们中原料的构成比例加权平均而得到。 对于多余的原料可以以每桶$9的价格售出。 a)决策变量是什么？ b)给出LP模型 c)要合成多少Premium? 参考解答： a)决策变量是两个产品中三种原材料的数量。分别用Lc,Li,Ls,Pc,Pi,Ps表示。 b) Model: !Lc,Li,工s,Pc,Pi,Ps表示两个产品中三种原材料的数量： !原材料限制： Lc+Pc<=2700;Li+Pi<=1350::Ls+Pc<=4100: !表示剩余原料：

5 F1 0.0000000 0.1035937E-02 F2 22.06205 0.0000000 A1 14.23886 0.0000000 A2 0.0000000 0.2050311E-01 A3 0.0000000 0.1992597E-01 CB 0.0000000 0.3356920E-02 S1 200.0000 0.0000000 S2 29.43496 0.0000000 S3 200.0000 0.0000000 注意，调和后的产品仅仅利用了 7 种原材料。 在实践中，匹斯堡公司基本上每月要运行两次。第一次运行结束后，采购商根据递减 成本和影子价格来指导购买原材料。第二次运行结束后，制造商就会从生产的产品中获得 收益。 5.3 案例及参考解答 5-1. 这个星期，Exxoff公司必须对合成汽油产品作出决定。他们要合成两种汽油产品， 产品的特性列表如下： 汽油产品 蒸汽压 辛烷数 售价(S/桶) Lo-lead <= 7 >= 80 $ 9.80 Premium <= 6 >= 100 $12.00 构成两种汽油的原料及它们的特性列表如下： 原料 蒸汽压 辛烷数 本周可供量(桶) Cat-Cracked Gas 8 83 2700 Isopentane 20 109 1350 Straight Gas 4 74 4100 汽油产品中的蒸汽压和辛烷数可简单地按照它们中原料的构成比例加权平均而得到。 对于多余的原料可以以每桶$9的价格售出。 a) 决策变量是什么? b) 给出LP模型 c) 要合成多少Premium? 参考解答： a) 决策变量是两个产品中三种原材料的数量。分别用Lc，Li，Ls，Pc，Pi，Ps表示。 b) Model: !Lc，Li，Ls，Pc，Pi，Ps表示两个产品中三种原材料的数量; !原材料限制; Lc+Pc<=2700; Li+Pi<=1350; Ls+Pc<=4100; !表示剩余原料;