《运筹学》课程教学资源（参考资料）3 网络计划模型

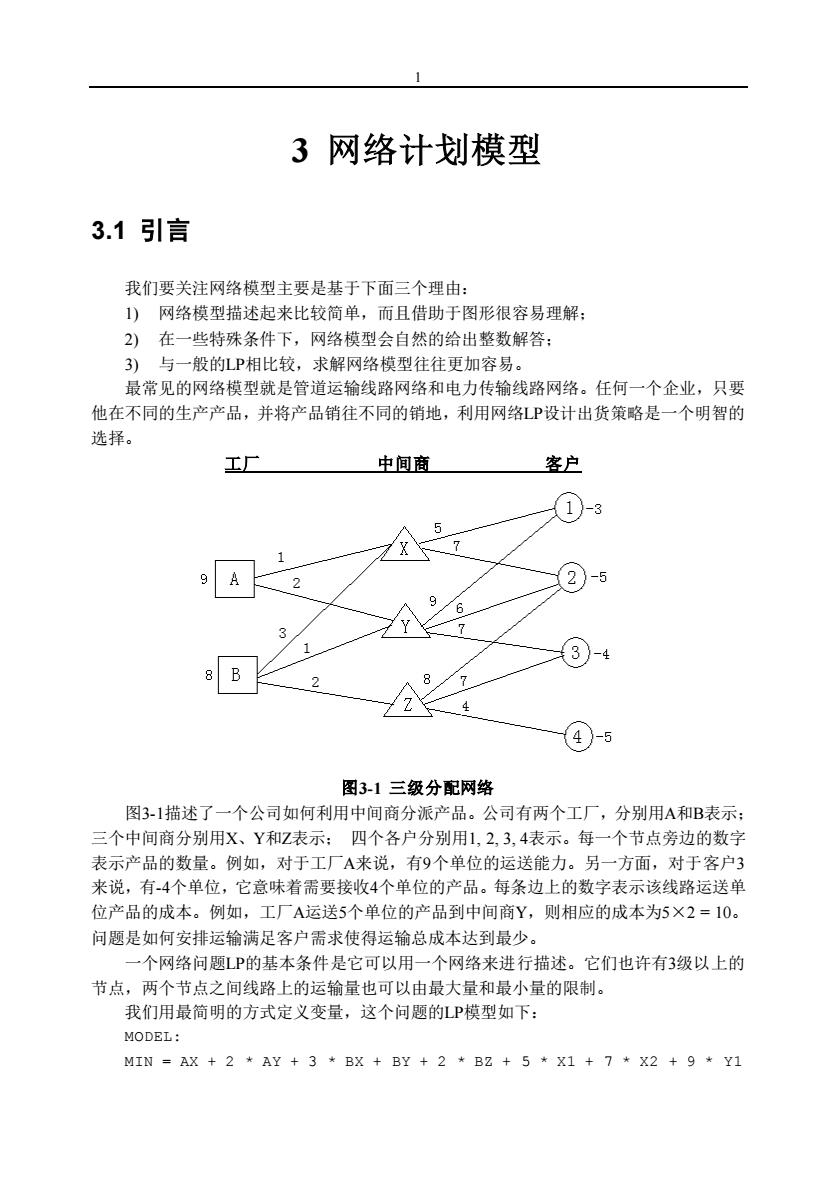
3网络计划模型 3.1引言 我们要关注网络模型主要是基于下面三个理由： 1)网络模型描述起来比较简单，而且借助于图形很容易理解： 2)在一些特殊条件下，网络模型会自然的给出整数解答： 3)与一般的LP相比较，求解网络模型往往更加容易。 最常见的网络模型就是管道运输线路网络和电力传输线路网络。任何一个企业，只要 他在不同的生产产品，并将产品销往不同的销地，利用网络LP设计出货策略是一个明智的 选择。 工厂 中间商 客户 -3 5 A 2 3-5 6 3 1 3 -4 B 2 图3-1三级分配网络 图3-1描述了一个公司如何利用中间商分派产品。公司有两个工厂，分别用A和B表示： 三个中间商分别用X、Y和Z表示：四个各户分别用1,2,3,4表示。每一个节点旁边的数字 表示产品的数量。例如，对于工厂A来说，有9个单位的运送能力。另一方面，对于客户3 来说，有-4个单位，它意味着需要接收4个单位的产品。每条边上的数字表示该线路运送单 位产品的成本。例如，工厂A运送5个单位的产品到中间商Y,则相应的成本为5×2=10。 问题是如何安排运输满足客户需求使得运输总成本达到最少。 一个网络问题LP的基本条件是它可以用一个网络来进行描述。它们也许有3级以上的 节点，两个节点之间线路上的运输量也可以由最大量和最小量的限制。 我们用最简明的方式定义变量，这个问题的LP模型如下： MODEL: MIN AX 2 AY 3 BX BY 2 BZ 5 X1 7 X2 9 Y1

1 3 网络计划模型 3.1 引言 我们要关注网络模型主要是基于下面三个理由： 1) 网络模型描述起来比较简单，而且借助于图形很容易理解； 2) 在一些特殊条件下，网络模型会自然的给出整数解答； 3) 与一般的LP相比较，求解网络模型往往更加容易。 最常见的网络模型就是管道运输线路网络和电力传输线路网络。任何一个企业，只要 他在不同的生产产品，并将产品销往不同的销地，利用网络LP设计出货策略是一个明智的 选择。 工厂 中间商 客户 图3-1 三级分配网络 图3-1描述了一个公司如何利用中间商分派产品。公司有两个工厂，分别用A和B表示； 三个中间商分别用X、Y和Z表示； 四个各户分别用1, 2, 3, 4表示。每一个节点旁边的数字 表示产品的数量。例如，对于工厂A来说，有9个单位的运送能力。另一方面，对于客户3 来说，有-4个单位，它意味着需要接收4个单位的产品。每条边上的数字表示该线路运送单 位产品的成本。例如，工厂A运送5个单位的产品到中间商Y，则相应的成本为5×2 = 10。 问题是如何安排运输满足客户需求使得运输总成本达到最少。 一个网络问题LP的基本条件是它可以用一个网络来进行描述。它们也许有3级以上的 节点，两个节点之间线路上的运输量也可以由最大量和最小量的限制。 我们用最简明的方式定义变量，这个问题的LP模型如下： MODEL: MIN = AX + 2 * AY + 3 * BX + BY + 2 * BZ + 5 * X1 + 7 * X2 + 9 * Y1

2 +6*Y2+7*Y3+8*Z2+7*Z3+4*Z4: AX AY 9; BX BY BZ 8; -AX-BX+X1+X2=0: -AY-BY+Y1+Y2+Y3=0; -BZ+Z2+Z3+Z4=0; -X1-Y1=-3: -X2-Y2-z2=-5: -Y3-Z3=-4; -Z4=-5; END 对于每一个节点来说，都有一个约束：“来源量=使用量”。例如，约束5是限制中间 商Y的，表明运出产品数量减去运入产品数量的结果为零。 下面列出了上面LP模型的系数矩阵，可以从另一个角度看出网络问题的结构。 AA BB BX XY YY Z ZZ X Y Z12 123 23 4 1: 1 2 2 2 57 9 67 87 4 MIN 2: 1 =9 3 1 =8 4: -1 -1 = 5 6 11 1 7 =-3 8: =5 9 =-4 10: -1=5 你也许注意到了一个网络问题约束矩阵的一个非常重要的特性。如果不靠个别变量的 界限约束，约束矩阵的每一列只有两个非零数，一个是+1，另一个是-1。下面给出这个问 题的解答： Optimal solution found at step: 1 Objective value: 121.0000 Variable Value Reduced Cost AX 3.000000 0.000000 AY 6.000000 0.000000 BX 0.000000 3.000000 BY 3.000000 0.000000 BZ 5.000000 0.000000 X1 3.000000 0.000000 X2 0.000000 0.000000 Y1 0.000000 5.000000

2 + 6 * Y2 + 7 * Y3 + 8 * Z2 + 7 * Z3 + 4 * Z4; AX + AY = 9; BX + BY + BZ = 8; - AX - BX + X1 + X2 = 0; - AY - BY + Y1 + Y2 + Y3 = 0; - BZ + Z2 + Z3 + Z4 = 0; - X1 - Y1 = -3; - X2 - Y2 - Z2 = -5; - Y3 - Z3 = -4; - Z4 = -5; END 对于每一个节点来说，都有一个约束：“来源量=使用量”。例如，约束 5 是限制中间 商 Y 的，表明运出产品数量减去运入产品数量的结果为零。 下面列出了上面 LP 模型的系数矩阵，可以从另一个角度看出网络问题的结构。 A X A Y B X B Y B Z X 1 X 2 Y 1 Y 2 Y 3 Z 2 Z 3 Z 4 1: 1 2 3 1 2 5 7 9 6 7 8 7 4 MIN 2: 1 1 = 9 3: 1 1 1 = 8 4: -1 -1 1 1 = 5: -1 -1 1 1 1 = 6: -1 1 1 1 = 7: -1 -1 = -3 8: -1 -1 -1 = -5 9: -1 -1 = -4 10: - 1 = -5 你也许注意到了一个网络问题约束矩阵的一个非常重要的特性。如果不靠个别变量的 界限约束，约束矩阵的每一列只有两个非零数，一个是+1，另一个是-1。下面给出这个问 题的解答： Optimal solution found at step: 1 Objective value: 121.0000 Variable Value Reduced Cost AX 3.000000 0.000000 AY 6.000000 0.000000 BX 0.000000 3.000000 BY 3.000000 0.000000 BZ 5.000000 0.000000 X1 3.000000 0.000000 X2 0.000000 0.000000 Y1 0.000000 5.000000

3 Y2 5.000000 0.000000 Y3 4.000000 0.000000 z2 0.000000 3.000000 z3 0.000000 1.000000 Z4 5.000000 0.000000 这个解答揭示了求解网络问题的两个特点是：： 1)如果约束右边的系数（生产能力或需求）是整数，那末变量也是整数。 2)如果目标函数系数是整数，那末对偶价格也是整数。 下面我们对网络LP做一个总结： ●与每一个节点对应的数字是节点的能力（负数表示需求）。 ●与每一条边对应的是： a)运送单位产品的成本（也可以是负数）： b)运送产品的最低数量（通常是0）： C)运送产品的最高数量（本例中是无穷大）。 我们的问题是在满足供应、需求和流量限制的条件下如何安排运输才能使得总成本最 小。 3.2典型案例 有一些普通的LP模型就是标准的网络LP案例。它们分别是： 1)运输问题。它是一个2级网络问题。所有的1级节点都是供应商。所有的2级 节点都是用户。供应商和用户之间只有一条线路。 2)最短路和最长路问题。假设已知美国的道路网络。人们希望能够找到从Bangor到 San Diego的最短距离。这个问题等价于从Bangor运送单位产品到San Diego的运输问题， 线路的运输成本就是线路的长度。关于最短路问题有简单而快速的计算程序。最短路问题 的姐妹问题就是在PERT或CPM分析中出现的最长路问题。 3)指派问题。如果一个运输问题中供应商的数量与用户的数量一样，每一个供应商 只提供一个产品而每一个用户只接受一个产品，这个运输问题就是指派问题。对于这个 问题己经出现高效率的计算程序。 4)最大流问题。给定一个有向网络，对于每一条线路有一个运输量的上限限制。人 们想知道从一个特定的出发点到一个特定的目的地的最大运输量是多少。这个问题可以用 于建筑运输和军事调动案例中。 在一个大型项目的管理过程中，计划评估法(PERT和关键线路法(CPM①是两个相关的 监控技术。PERT/CPM的关键是计算关键线路，就是确定一些必须按时完成的活动以保证 整个项目按期完成。 我们将通过例子来说明：关键线路的计算是一个很简单的网络LP问题。再具体一点 说关键线路就是一个最长的线路。 在下面的表格中，我们列出了建设一栋房子的主要作业。一项作业只有在他的所有 紧前作业完成之后才可以进行

3 Y2 5.000000 0.000000 Y3 4.000000 0.000000 Z2 0.000000 3.000000 Z3 0.000000 1.000000 Z4 5.000000 0.000000 这个解答揭示了求解网络问题的两个特点是：: 1）如果约束右边的系数（生产能力或需求）是整数，那末变量也是整数。 2）如果目标函数系数是整数，那末对偶价格也是整数。 下面我们对网络 LP 做一个总结： ⚫ 与每一个节点对应的数字是节点的能力（负数表示需求）。 ⚫ 与每一条边对应的是： a) 运送单位产品的成本（也可以是负数）； b) 运送产品的最低数量（通常是 0）； c) 运送产品的最高数量（本例中是无穷大）。 我们的问题是在满足供应、需求和流量限制的条件下如何安排运输才能使得总成本最 小。 3.2 典型案例 有一些普通的 LP 模型就是标准的网络 LP 案例。 它们分别是： 1） 运输问题。它是一个 2 级网络问题。所有的 1 级节点都是供应商。 所有的 2 级 节点都是用户。供应商和用户之间只有一条线路。 2） 最短路和最长路问题。假设已知美国的道路网络。人们希望能够找到从 Bangor 到 San Diego 的最短距离。这个问题等价于从 Bangor 运送单位产品到 San Diego 的运输问题， 线路的运输成本就是线路的长度。关于最短路问题有简单而快速的计算程序。最短路问题 的姐妹问题就是在 PERT 或 CPM 分析中出现的最长路问题。 3） 指派问题。如果一个运输问题中供应商的数量与用户的数量一样，每一个供应商 只提供一个产品而每一个用户只接受一个产品， 这个运输问题就是指派问题。对于这个 问题已经出现高效率的计算程序。 4） 最大流问题。给定一个有向网络，对于每一条线路有一个运输量的上限限制。人 们想知道从一个特定的出发点到一个特定的目的地的最大运输量是多少。这个问题可以用 于建筑运输和军事调动案例中。 在一个大型项目的管理过程中，计划评估法(PERT)和关键线路法(CPM)是两个相关的 监控技术。PERT/CPM 的关键是计算关键线路，就是确定一些必须按时完成的活动以保证 整个项目按期完成。 我们将通过例子来说明: 关键线路的计算是一个很简单的网络 LP 问题。再具体一点 说关键线路就是一个最长的线路。 在下面的表格中，我们列出了建设一栋房子的主要作业。 一项作业只有在他的所有 紧前作业完成之后才可以进行

4 作业 记号 作业时间 紧前作业 挖地基 DIG 浇灌基础 FOUND 4 DIG 浇灌地面 POURB 2 FOUND 安装拖梁 JOISTS 3 FOUND 安装围墙 WALLS 5 FOUND 安装椽子 RAFTERS 3 WALLS,POURB 安装地板 FLOOR 4 JOISTS 内部初装修 ROUGH 6 FLOOR 安装屋顶 ROOF 7 RAFTERS 内部精装修 FINISH 5 ROUGH.ROOF 美化环境 SCAPE 2 POURB,WALLS 在图3-1中，我们将说明这个项目的PET网络（箭线式网络）。我们将通过计算最少 的占用时间来完成这项工作。对于图3-1，我们对从左到右最长线路的长度感兴趣。如果 这个线路上的作业不能按时完成，那末这个项目就不能按时完成。经检验，关键线路由DIG, FOUND,WALLS,RAFTERS,ROOF和FINISH组成，长度为27。 虽然这个例子可以不用计算机来完成，但是我们还是来学习如何用公式来描述这个问 题，从而来用LP模型来求解。 Rough Floor 6 4 H Roof Joists 7 Finish 3 5 G Dig B Found Pour B 3 4 Rafters 2 3 Scape 5 2 Walls 图3-1建设一栋房子的网络图 首先定义变量DIG只取0或1用来表示作业DIG是否在关键线路上。对于其他的变 量也类似。等于1的变量就构成了关键线路。相应的目标函数就在PERT图中找出最长的 线路。 目标函数是： MAX 3 DIG +4 FOUND 2 POURB 3 JOISTS 5 WALLS 3 RAFTERS +4 FLOOR +6 ROUGH +7 ROOF 5 FINISH +2 SCAPE; 单就目标函数本身来说似乎有问题。我们并不是要求出项目的最大长度。当然，如果 我们适当地增加约束，我们将会看到这个目标函数就是求出了这个PET网络的最长线路。 增加的线路如下： 1)作业DG一定在关键线路上：

4 作业 记号 作业时间 紧前作业 挖地基 DIG 3 — 浇灌基础 FOUND 4 DIG 浇灌地面 POURB 2 FOUND 安装拖梁 JOISTS 3 FOUND 安装围墙 WALLS 5 FOUND 安装椽子 RAFTERS 3 WALLS, POURB 安装地板 FLOOR 4 JOISTS 内部初装修 ROUGH 6 FLOOR 安装屋顶 ROOF 7 RAFTERS 内部精装修 FINISH 5 ROUGH, ROOF 美化环境 SCAPE 2 POURB, WALLS 在图 3-1 中，我们将说明这个项目的 PERT 网络(箭线式网络) 。我们将通过计算最少 的占用时间来完成这项工作。对于图 3-1，我们对从左到右最长线路的长度感兴趣。如果 这个线路上的作业不能按时完成，那末这个项目就不能按时完成。经检验，关键线路由 DIG, FOUND, WALLS, RAFTERS, ROOF 和 FINISH 组成，长度为 27。 虽然这个例子可以不用计算机来完成，但是我们还是来学习如何用公式来描述这个问 题，从而来用 LP 模型来求解。 图 3-1 建设一栋房子的网络图 首先定义变量 DIG 只取 0 或 1 用来表示作业 DIG 是否在关键线路上。对于其他的变 量也类似。等于 1 的变量就构成了关键线路。相应的目标函数就在 PERT 图中找出最长的 线路。 目标函数是： MAX = 3 * DIG + 4 * FOUND + 2 * POURB + 3 * JOISTS + 5 * WALLS + 3 * RAFTERS + 4 * FLOOR + 6 * ROUGH + 7 * ROOF + 5 * FINISH + 2 * SCAPE; 单就目标函数本身来说似乎有问题。我们并不是要求出项目的最大长度。当然，如果 我们适当地增加约束，我们将会看到这个目标函数就是求出了这个 PERT 网络的最长线路。 增加的线路如下： 1) 作业 DIG 一定在关键线路上；

2)一个作业只有在它的紧前作业在关键线路上时它才可以在关键线路上。进一步说， 如果一个作业有紧后作业，只有在它的紧后作也在关键线路上时它才可以在关键线路上。 3)作业SCAPE或FINISH必定有一个在关键线路上。 通过加入下面的约束就可以实现上面的要求： -DIG=-1: FOUND DIG 0 JOISTS -POURB WALLS FOUND =0; FLOOR JOISTS =0; RAFTERS SCAPE POURB WALLS =0; ROUGH FLOOR 0; ROOF RAFTERS 0; FINISH ROUGH ROOF 0; FINISH SCAPE +1; 这个问题的解答如下： Optimal solution found at step: 2 Objective value: 27.00000 Variable Value Reduced Cost DIG 1.000000 0.000000 FOUND 1.000000 0.000000 POURB 0.000000 3.000000 JOISTS 0.000000 0.000000 WALLS 1.000000 0.000000 RAFTERS 1.000000 0.000000 FLOOR 0.000000 0.000000 ROUGH 0.000000 2.000000 ROOF 1.000000 0.000000 FINISH 1.000000 0.000000 SCAPE 0.000000 13.00000 注意关键线路上作业对应变量的值都是1。如果第一个约束“DIG=-1”被删除，结 果会如何？ 看看下面这个问题的系数结构也很有好处： R W F 0 0 G D D R H E 1: 6 2 MAX

5 2) 一个作业只有在它的紧前作业在关键线路上时它才可以在关键线路上。进一步说， 如果一个作业有紧后作业，只有在它的紧后作也在关键线路上时它才可以在关键线路上。. 3) 作业 SCAPE 或 FINISH 必定有一个在关键线路上。 通过加入下面的约束就可以实现上面的要求： - DIG = -1; - FOUND + DIG = 0; - JOISTS - POURB - WALLS + FOUND = 0; - FLOOR + JOISTS = 0; - RAFTERS - SCAPE + POURB + WALLS = 0; - ROUGH + FLOOR = 0; - ROOF + RAFTERS = 0; - FINISH + ROUGH + ROOF = 0; + FINISH + SCAPE = +1; 这个问题的解答如下： Optimal solution found at step: 2 Objective value: 27.00000 Variable Value Reduced Cost DIG 1.000000 0.000000 FOUND 1.000000 0.000000 POURB 0.000000 3.000000 JOISTS 0.000000 0.000000 WALLS 1.000000 0.000000 RAFTERS 1.000000 0.000000 FLOOR 0.000000 0.000000 ROUGH 0.000000 2.000000 ROOF 1.000000 0.000000 FINISH 1.000000 0.000000 SCAPE 0.000000 13.00000 注意关键线路上作业对应变量的值都是 1。如果第一个约束“-DIG = - 1”被删除，结 果会如何？ 看看下面这个问题的系数结构也很有好处： D I G F O U N D P O U N D J O I S T S W A L L S R A F T E R S F L O O R R O U G H R O O F F N I S H S C A P E 1: 3 4 2 3 5 3 4 6 7 5 2 MAX