
6 Lc+Pc+Y11=2700:Li+Pi+Y21=1350: Ls+Pc+Y31=4100: !质量要求; 8*Lc+20*Li+4*Ls<7*(Lc+L1+Ls): 83*Lc+109*Li+74*Ls>80*(Lc+Li+Ls): 8*Pc+20*Pi+4*Ps 6*(Pc+Pi+Ps); 83*Pc+109*Pi+74*Ps>100*(Pc+Pi+Ps): !目标; max=9.8*(Lc+Li+Ls)+12*(Pc+Pi+Ps)+9*(Y11+Y21+Y31): @gin(Lc);@gin(Li);@gin(Ls);@gin(Pc);@gin(Pi);@gin(Ps); c)不合成Premium。合成Lo-lead7538桶,总利润79380.40美元。 End 5-2.Blendex石油公司用庚烷(Heptane)和辛烷(Octane)两种原料合成Regular和Premium 两种产品。每一升Regulari产品由50%庚烷和50%辛烷合成,每升Premium产品由40%庚烷与 60%辛烷组成。在生产计划期内,共有200,000升庚烷,310,000升辛烷的原料。每升Regular 和Premium的利润分别为0.03美元,0.04美元。 a)为了确定出Regular和Premium的产量,试建立相应的线性规划模型。 b)不使用计算机计算出最优产量。 参考解答: )分别用H和O表示两种原料的数量,用R和P表示两个产品的数量。模型如下: Model: !分别用RH,RO和PH,PO表示两个产品中两种原料的数量; !原材料限制; RH+PH<20;R0+P0<31;!单位是万升: !质量要求; RH=RO;4*PO=6*PH; !目标; max=0.03*(RH+R0)+0.04*(P0+PH); End b)利用质量要求消去两个变量,用图解法求得最优解:PH=20,PO=30,故生产 Premium50万升,总利润为2万美元。 S-3.Hackensack调和威士忌酒业公司进口Prime、Choice和Premium三个等级的威士忌 原料酒。将这些原料酒混合起来就可以生产出两个品牌的威士忌产品。 相关的质量指标是: 品牌 规格 售价($L) 苏格兰俱乐部 Prime≥60%且Premium≤20% $S6.80 约翰尼.金 Prime≥15%且Premium≤60% $5.70 三个等级原料酒的成本和供应量如下: 威士忌原料酒 本周供应量(L) 单价($L) Prime 2,000 $7.00 Choice 2,500 $5.00 Premium 1,200 $4.00
6 Lc+Pc+Y11=2700; Li+Pi+Y21=1350; Ls+Pc+Y31=4100; !质量要求; 8*Lc+ 20*Li+ 4*Ls < 7*(Lc+Li+Ls); 83*Lc+109*Li+74*Ls > 80*(Lc+Li+Ls); 8*Pc+ 20*Pi+ 4*Ps < 6*(Pc+Pi+Ps); 83*Pc+109*Pi+74*Ps >100*(Pc+Pi+Ps); !目标; max=9.8*(Lc+Li+Ls)+12*(Pc+Pi+Ps)+9*(Y11+Y21+Y31); @gin(Lc);@gin(Li);@gin(Ls);@gin(Pc);@gin(Pi);@gin(Ps); c) 不合成Premium。合成Lo-lead7538桶,总利润79380.40美元。 End 5-2. Blendex石油公司用庚烷(Heptane)和辛烷(Octane)两种原料合成Regular和Premium 两种产品。每一升Regular产品由50%庚烷和50%辛烷合成,每升Premium产品由40%庚烷与 60%辛烷组成。在生产计划期内,共有200,000升庚烷,310,000升辛烷的原料。每升Regular 和Premium的利润分别为0.03美元,0.04美元。 a) 为了确定出Regular和Premium的产量,试建立相应的线性规划模型。 b) 不使用计算机计算出最优产量。 参考解答: a) 分别用H和O表示两种原料的数量,用R和P表示两个产品的数量。模型如下: Model: !分别用RH,RO和PH,PO表示两个产品中两种原料的数量; !原材料限制; RH+PH<20; RO+PO<31; !单位是万升; !质量要求; RH=RO; 4*PO=6*PH; !目标; max=0.03*(RH+RO)+0.04*(PO+PH); End b) 利用质量要求消去两个变量,用图解法求得最优解:PH=20,PO=30,故生产 Premium50万升,总利润为2万美元。 5-3. Hackensack调和威士忌酒业公司进口Prime、Choice和Premium三个等级的威士忌 原料酒。将这些原料酒混合起来就可以生产出两个品牌的威士忌产品。 相关的质量指标是: 品牌 规格 售价($/L) 苏格兰.俱乐部 Prime≥60%且Premium≤20% $6.80 约翰尼.金 Prime≥15%且Premium≤60% $5.70 三个等级原料酒的成本和供应量如下: 威士忌原料酒 本周供应量(L) 单价($/L) Prime 2,000 $7.00 Choice 2,500 $5.00 Premium 1,200 $4.00

Hackensac公司希望本周公司的利润达到最大化,而且认为可以利用线性规划来完成 相关的计算。两种品牌的产品各生产多少?产品的结构(三种原料的构成)如何? 参考解答: Model: Sets: brand/scottish johnny /price,product; !品牌集合,有两个集合成员,共有属性为单价,生产量: stock/Prime Choice Premium/:supply,cost,number; !原料集合,有三个成员,所含属性有周可用量,成本单价,所需量: b_s(stock,brand):ounce,result; !派生集合,由品牌和原料派生而成的,属性有原料的要求,结果: Endsets data: price=@0LE('最优化案例5-3.xls','price'): supp1y=@oLE('最优化案例5-3.x1s','supply'): cost=@0LE('最优化案例5-3.x1s','cost'): ounce=eoLE('最优化案例5-3.xls','ounce'): enddata !以上用来将excel中数据输入到1ingo中。: @for(stock(i): number(i)=@sum(bs(i,j):result (i,j))); !各原料的总量: @for(brand(j): product(j)=@sum(b s(i,j):result(i,j))); !各产品的总量: max=@sum(brand(j):price(j)*product (j))-@sum(stock (i)cost (i)*num ber(i)); !目标函数: @for(stock(i): @sum(b_s(i,j)result (i,j))<=supply(i)); !约束一,表示各原料小于等于每周可用量: @for(b_s(i,j)li#eq#1: result(i,j)>=ounce(i,j)*@sum(b_s(k,j)result (k,j))); !第一行的约束: @for(b_s(i,j)li#eq#3: result (i,j)<=ounce(i,j)*@sum(b_s(k,j)result (k,j))); !第三行的约束: data: @0LB('最优化案例5-3.xls','result')=result; @oLB('最优化案例5-3.xls','number')=number;
7 Hackensac公司希望本周公司的利润达到最大化,而且认为可以利用线性规划来完成 相关的计算。两种品牌的产品各生产多少?产品的结构(三种原料的构成)如何? 参考解答: Model: Sets: brand/scottish johnny /: price,product; !品牌集合,有两个集合成员,共有属性为单价,生产量; stock/Prime Choice Premium/: supply,cost,number; !原料集合,有三个成员,所含属性有周可用量,成本单价,所需量; b_s(stock,brand):ounce,result; !派生集合,由品牌和原料派生而成的,属性有原料的要求,结果; Endsets data: price=@OLE('最优化案例5-3.xls','price'); supply=@OLE('最优化案例5-3.xls','supply'); cost=@OLE('最优化案例5-3.xls','cost'); ounce=@OLE('最优化案例5-3.xls','ounce'); enddata !以上用来将excel中数据输入到lingo中。; @for(stock(i): number(i)=@sum(b_s(i,j):result(i,j))); !各原料的总量; @for(brand(j): product(j)=@sum(b_s(i,j):result(i,j))); !各产品的总量; max=@sum(brand(j):price(j)*product(j))-@sum(stock(i):cost(i)*num ber(i)); !目标函数; @for(stock(i): @sum(b_s(i,j):result(i,j))<=supply(i)); !约束一,表示各原料小于等于每周可用量; @for(b_s(i,j)|i#eq#1: result(i,j)>=ounce(i,j)*@sum(b_s(k,j):result(k,j))); !第一行的约束; @for(b_s(i,j)|i#eq#3: result(i,j)<=ounce(i,j)*@sum(b_s(k,j):result(k,j))); !第三行的约束; data: @OLE('最优化案例5-3.xls','result')=result; @OLE('最优化案例5-3.xls','number')=number;
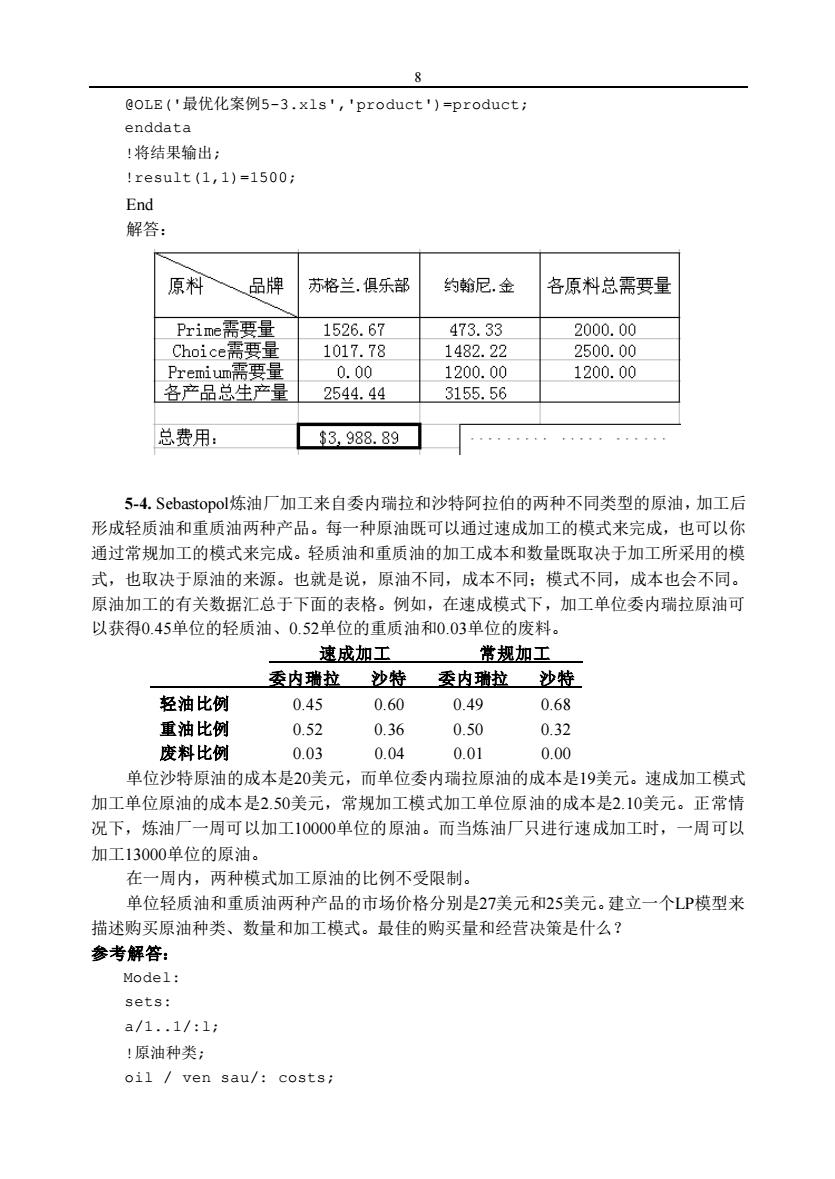
@oLE('最优化案例5-3.xls','product')=product; enddata !将结果输出 !resu1t(1,1)=1500: End 解答: 原料 品牌 苏格兰,俱乐部 约翰尼.金 各原料总需要量 Prime需要量 1526.67 473.33 2000.00 Choice需要量 1017.78 1482.22 2500.00 Premiumi需要量 0.00 1200.00 1200.00 各产品总生产量 2544.44 3155.56 总费用: $3,988.89 5-4.Sebastopol炼油厂加工来自委内瑞拉和沙特阿拉伯的两种不同类型的原油,加工后 形成轻质油和重质油两种产品。每一种原油既可以通过速成加工的模式来完成,也可以你 通过常规加工的模式来完成。轻质油和重质油的加工成本和数量既取决于加工所采用的模 式,也取决于原油的来源。也就是说,原油不同,成本不同:模式不同,成本也会不同。 原油加工的有关数据汇总于下面的表格。例如,在速成模式下,加工单位委内瑞拉原油可 以获得0.45单位的轻质油、0.52单位的重质油和0.03单位的废料。 速成加工 常规加工 委内瑞拉 沙特 委内瑞拉沙特」 轻油比例 0.45 0.60 0.49 0.68 重油比例 0.52 0.36 0.50 0.32 废料比例 0.03 0.04 0.01 0.00 单位沙特原油的成本是20美元,而单位委内瑞拉原油的成本是19美元。速成加工模式 加工单位原油的成本是2.50美元,常规加工模式加工单位原油的成本是2.10美元。正常情 况下,炼油厂一周可以加工10000单位的原油。而当炼油厂只进行速成加工时,一周可以 加工13000单位的原油。 在一周内,两种模式加工原油的比例不受限制。 单位轻质油和重质油两种产品的市场价格分别是27美元和25美元。建立一个LP模型来 描述购买原油种类、数量和加工模式。最佳的购买量和经营决策是什么? 参考解答: Model: sets: a/1.1/:1: !原油种类; oil ven sau/:costs;
8 @OLE('最优化案例5-3.xls','product')=product; enddata !将结果输出; !result(1,1)=1500; End 解答: 5-4. Sebastopol炼油厂加工来自委内瑞拉和沙特阿拉伯的两种不同类型的原油,加工后 形成轻质油和重质油两种产品。每一种原油既可以通过速成加工的模式来完成,也可以你 通过常规加工的模式来完成。轻质油和重质油的加工成本和数量既取决于加工所采用的模 式,也取决于原油的来源。也就是说,原油不同,成本不同;模式不同,成本也会不同。 原油加工的有关数据汇总于下面的表格。例如,在速成模式下,加工单位委内瑞拉原油可 以获得0.45单位的轻质油、0.52单位的重质油和0.03单位的废料。 速成加工 常规加工 委内瑞拉 沙特 委内瑞拉 沙特 轻油比例 0.45 0.60 0.49 0.68 重油比例 0.52 0.36 0.50 0.32 废料比例 0.03 0.04 0.01 0.00 单位沙特原油的成本是20美元,而单位委内瑞拉原油的成本是19美元。速成加工模式 加工单位原油的成本是2.50美元,常规加工模式加工单位原油的成本是2.10美元。正常情 况下,炼油厂一周可以加工10000单位的原油。而当炼油厂只进行速成加工时,一周可以 加工13000单位的原油。 在一周内,两种模式加工原油的比例不受限制。 单位轻质油和重质油两种产品的市场价格分别是27美元和25美元。建立一个LP模型来 描述购买原油种类、数量和加工模式。最佳的购买量和经营决策是什么? 参考解答: Model: sets: a/1.1/:l; !原油种类; oil / ven sau/: costs;

9 !处理方式: process short regular/:cost; !产成品: products light heavy /price; po(process,oil):use; !三者的派生集合: ppo(products process,oil):precent; !周产量限制数据; capacity 1.2/:amount; endsets data: costs=@0LE('最优化案例5-4.x1s'): cost=@0LB('最优化案例5-4.x1s'); price=@0LE('最优化案例5-4.xls'): precent=@oLE('最优化案例5-4.xls'); amount:=eoLE('最优化案例5-4.xls'); @0LE('最优化案例5-4.x1s')=use; @0LE('最优化案例5-4.x1s')=1; enddata !约束: @sum(oil(i)use(1,i))+@sum(oil(i)use(2,i))*1.3<amount (1); !目标函数: max=1(1): 1(1)=@sum(products(k):@sum(po(i,j)use(i,j)*precent (k,i,j))*pric e(k)) -@sum(oil(i)@sum(process(j)use(j,i))*costs(i)) -@sum(process(i)@sum(oil(j):use(i,j))*cost(i)); use(2,2)=10000; End 解答: 快速处理 正常处理 委内瑞拉 沙特阿拉伯 委内瑞拉 沙特阿拉伯 轻型产品 5850.00 0.00 0.00 0.00 重型产品 6760.00 0.00 0.00 0.00 委内瑞拉 沙特阿拉伯 快速处理13000.00 0.00 总利润: $47,450.00 正常处理 0.00 0.00
9 !处理方式; process / short regular/: cost; !产成品; products / light heavy /: price; po(process,oil):use; !三者的派生集合; ppo(products ,process,oil): precent; !周产量限制数据; capacity / 1.2/: amount; endsets data: costs=@OLE('最优化案例5-4.xls'); cost=@OLE('最优化案例5-4.xls'); price=@OLE('最优化案例5-4.xls'); precent=@OLE('最优化案例5-4.xls'); amount=@OLE('最优化案例5-4.xls'); @OLE('最优化案例5-4.xls')=use; @OLE('最优化案例5-4.xls')=l; enddata !约束; @sum(oil(i):use(1,i))+@sum(oil(i):use(2,i))*1.3<amount(1); !目标函数; max=l(1); l(1)=@sum(products(k):@sum(po(i,j):use(i,j)*precent(k,i,j))*pric e(k)) -@sum(oil(i):@sum(process(j):use(j,i))*costs(i)) -@sum(process(i):@sum(oil(j):use(i,j))*cost(i)); use(2,2)=10000; End 解答:
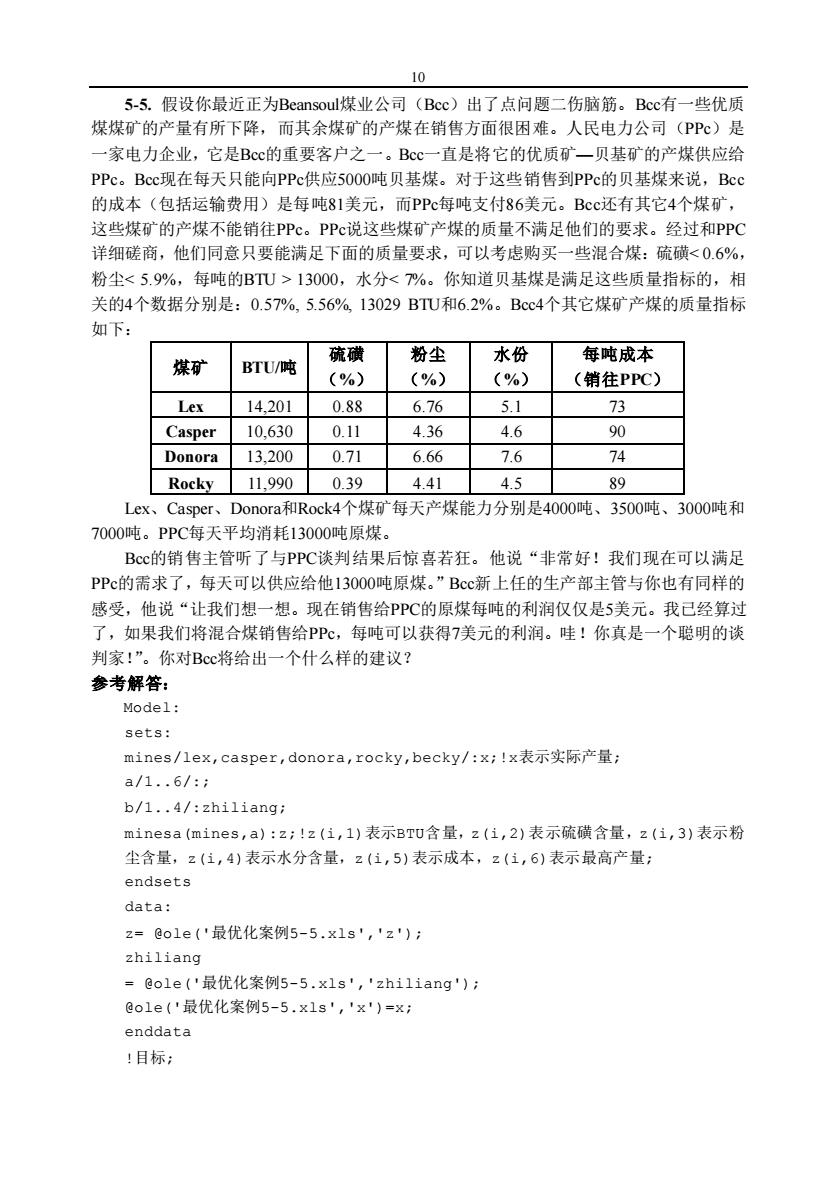
10 5-5.假设你最近正为Beansoul煤业公司(Bcc)出了点问题二伤脑筋。Bcc有一些优质 煤煤矿的产量有所下降,而其余煤矿的产煤在销售方面很困难。人民电力公司(PP℃)是 一家电力企业,它是Bcc的重要客户之一。Bcc一直是将它的优质矿一贝基矿的产煤供应给 PPC。Bcc现在每天只能向PPc供应5OOO吨贝基煤。对于这些销售到PPc的贝基煤来说,Bcc 的成本(包括运输费用)是每吨81美元,而PPc每吨支付86美元。BCc还有其它4个煤矿, 这些煤矿的产煤不能销往PPC。PPc说这些煤矿产煤的质量不满足他们的要求。经过和PPC 详细磋商,他们同意只要能满足下面的质量要求,可以考虑购买一些混合煤:硫磺<0.6%, 粉尘<5.9%,每吨的BTU>13000,水分<7%。你知道贝基煤是满足这些质量指标的,相 关的4个数据分别是:0.57%,5.56%,13029BTU和6.2%。Bcc4个其它煤矿产煤的质量指标 如下: 疏磺 粉尘 每吨成本 煤矿 水份 BTU/吨 (%) (%) (%) (销往PPC) Lex 14,201 0.88 6.76 5.1 73 Casper 10,630 0.11 4.36 4.6 90 Donora 13,200 0.71 6.66 7.6 74 Rocky 11.990 0.39 4.41 4.5 89 Lex、Casper、Donora和Rock4个煤矿每天产煤能力分别是4000吨、3500吨、3000吨和 7000吨。PPC每天平均消耗13000吨原煤。 BCc的销售主管听了与PPC谈判结果后惊喜若狂。他说“非常好!我们现在可以满足 PPc的需求了,每天可以供应给他13000吨原煤。”Bcc新上任的生产部主管与你也有同样的 感受,他说“让我们想一想。现在销售给PPC的原煤每吨的利润仅仅是5美元。我已经算过 了,如果我们将混合煤销售给PP℃,每吨可以获得7美元的利润。哇!你真是一个聪明的谈 判家!”。你对BCc将给出一个什么样的建议? 参考解答: Model: sets: mines/1ex,casper,donora,rocky,becky./:x;!x表示实际产量; a/1.6/:: b/1.4/:zhiliang; minesa(mines,a):z;!z(i,1)表示BTU含量,z(i,2)表示疏磺含量,z(i,3)表示粉 尘含量,z(1,4)表示水分含量,z(1,5)表示成本,z(1,6)表示最高产量: endsets data: z=@o1e('最优化案例5-5.x1s','z'): zhiliang =eo1e('最优化案例5-5.xls','zhi1iang'): @o1e('最优化案例5-5.x1s','x')=x: enddata !目标;
10 5-5. 假设你最近正为Beansoul煤业公司(Bcc)出了点问题二伤脑筋。Bcc有一些优质 煤煤矿的产量有所下降,而其余煤矿的产煤在销售方面很困难。人民电力公司(PPc)是 一家电力企业,它是Bcc的重要客户之一。Bcc一直是将它的优质矿—贝基矿的产煤供应给 PPc。Bcc现在每天只能向PPc供应5000吨贝基煤。对于这些销售到PPc的贝基煤来说,Bcc 的成本(包括运输费用)是每吨81美元,而PPc每吨支付86美元。Bcc还有其它4个煤矿, 这些煤矿的产煤不能销往PPc。PPc说这些煤矿产煤的质量不满足他们的要求。经过和PPC 详细磋商,他们同意只要能满足下面的质量要求,可以考虑购买一些混合煤:硫磺< 0.6%, 粉尘< 5.9%,每吨的BTU > 13000,水分< 7%。你知道贝基煤是满足这些质量指标的,相 关的4个数据分别是:0.57%, 5.56%, 13029 BTU和6.2%。Bcc4个其它煤矿产煤的质量指标 如下: 煤矿 BTU/吨 硫磺 (%) 粉尘 (%) 水份 (%) 每吨成本 (销往PPC) Lex 14,201 0.88 6.76 5.1 73 Casper 10,630 0.11 4.36 4.6 90 Donora 13,200 0.71 6.66 7.6 74 Rocky 11,990 0.39 4.41 4.5 89 Lex、Casper、Donora和Rock4个煤矿每天产煤能力分别是4000吨、3500吨、3000吨和 7000吨。PPC每天平均消耗13000吨原煤。 Bcc的销售主管听了与PPC谈判结果后惊喜若狂。他说“非常好!我们现在可以满足 PPc的需求了,每天可以供应给他13000吨原煤。”Bcc新上任的生产部主管与你也有同样的 感受,他说“让我们想一想。现在销售给PPC的原煤每吨的利润仅仅是5美元。我已经算过 了,如果我们将混合煤销售给PPc,每吨可以获得7美元的利润。哇!你真是一个聪明的谈 判家!”。你对Bcc将给出一个什么样的建议? 参考解答: Model: sets: mines/lex,casper,donora,rocky,becky/:x;!x表示实际产量; a/1.6/:; b/1.4/:zhiliang; minesa(mines,a):z;!z(i,1)表示BTU含量,z(i,2)表示硫磺含量,z(i,3)表示粉 尘含量,z(i,4)表示水分含量,z(i,5)表示成本,z(i,6)表示最高产量; endsets data: z= @ole('最优化案例5-5.xls','z'); zhiliang = @ole('最优化案例5-5.xls','zhiliang'); @ole('最优化案例5-5.xls','x')=x; enddata !目标;