
运筹学教程 第一章习题解 max Z=2x+x2 3x1+5x2≤15 (2) st.6x1+2x2≤24 x1,x2≥0 x2 (0,3) (3.75,0.75) ≥x1 (0,0) 4,0) page 12 23 April 2025 School of Management
运筹学教程 School of Management page 12 23 April 2025 第一章习题解答 + + = + , 0 6 2 24 3 5 15 . max 2 (2) 1 2 1 2 1 2 1 2 x x x x x x st Z x x
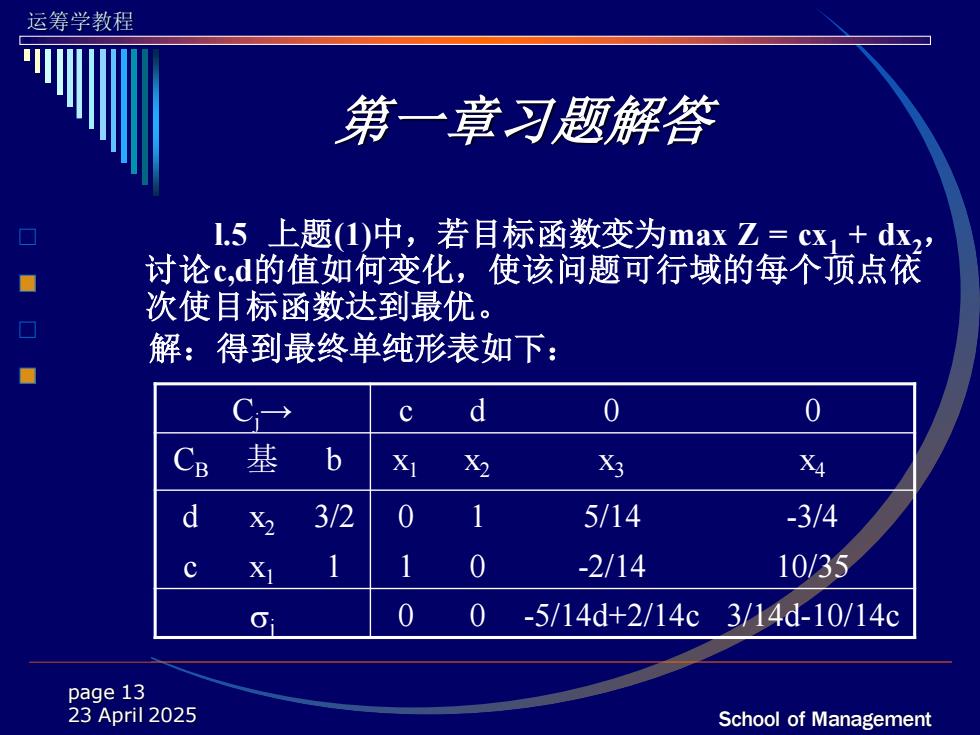
运筹学教程 第一章习题解答 l.5上题(1)中,若目标函数变为maxZ=cx1+dx2 讨论c,d的值如何变化,使该问题可行域的每个顶点依 次使目标函数达到最优。 解:得到最终单纯形表如下: c d 0 0 基b X1 X2 Xg X4 d X2 3/2 1 5/14 -3/4 X 1 0 -2/14 10/35 0 -5/14d+2/14c3/14d-10/14c page 13 23 April 2025 School of Management
运筹学教程 School of Management page 13 23 April 2025 第一章习题解答 l.5 上题(1)中,若目标函数变为max Z = cx1 + dx2, 讨论c,d的值如何变化,使该问题可行域的每个顶点依 次使目标函数达到最优。 解:得到最终单纯形表如下: Cj→ c d 0 0 CB 基 b x1 x2 x3 x4 d x2 3/2 0 1 5/14 -3/4 c x1 1 1 0 -2/14 10/35 j 0 0 -5/14d+2/14c 3/14d-10/14c
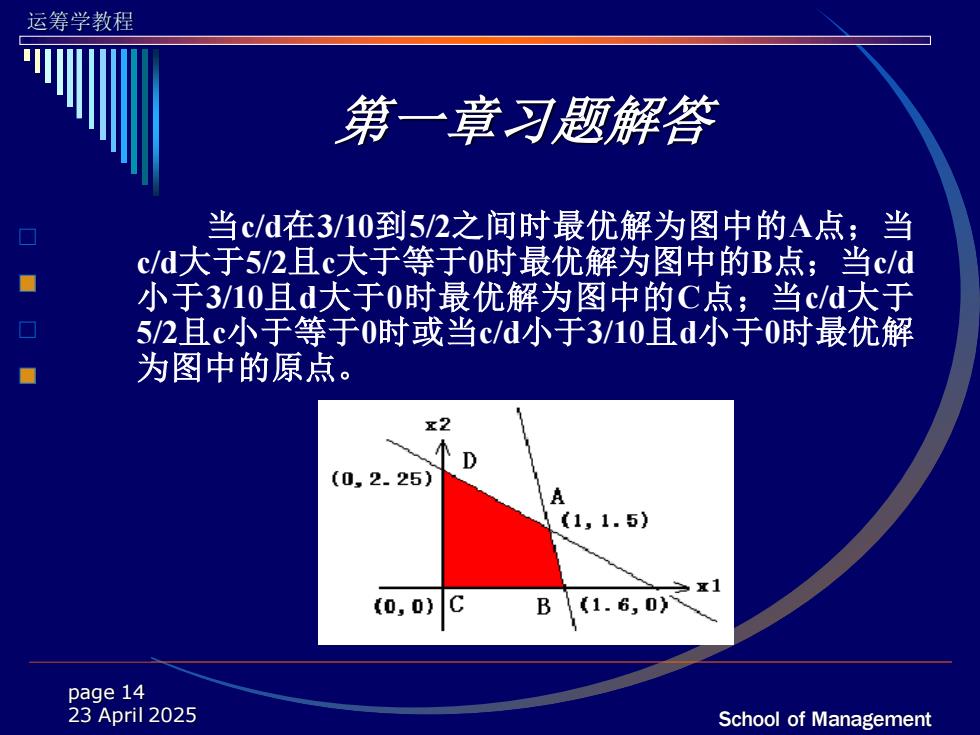
运筹学教程 第一章习题解答 当c/d在3/10到5/2之间时最优解为图中的A点;当 c/d大于5/2且c大于等于0时最优解为图中的B点;当c/d 小于3/10且d大于0时最优解为图中的C点;当c/d大于 5/2且c小于等于0时或当c/d小于3/10且d小于0时最优解 为图中的原点。 x2 D (0,2.25) A 《1,1.5) x1 (0,0) B1.6,0 page 14 23 April 2025 School of Management
运筹学教程 School of Management page 14 23 April 2025 第一章习题解答 当c/d在3/10到5/2之间时最优解为图中的A点;当 c/d大于5/2且c大于等于0时最优解为图中的B点;当c/d 小于3/10且d大于0时最优解为图中的C点;当c/d大于 5/2且c小于等于0时或当c/d小于3/10且d小于0时最优解 为图中的原点

运筹学教程 第一章习题解答 1.6考虑下述线性规划问题: max Z=Cx+C2x2 a11x1+a12x2≤b1 Sta21X1+a22x2≤b2 x1,x2≥0 式中,1≤c,≤3,4≤c2≤6,-1≤a1≤3,2≤a2≤5, 8≤b1≤12,2≤a21≤5,4≤a22≤6,10≤b2≤14,试确定 目标函数最优值的下界和上界。 page 15 23 April 2025 School of Management
运筹学教程 School of Management page 15 23 April 2025 第一章习题解答 式中,1≤c1≤3, 4≤c2≤6, -1≤a11≤3, 2≤a12≤5, 8≤b1≤12, 2≤a21≤5, 4≤a22≤6, 10≤b2≤14,试确定 目标函数最优值的下界和上界。 + + = + , 0 . max 1 2 21 1 22 2 2 11 1 12 2 1 1 1 2 2 x x a x a x b a x a x b st Z c x c x l.6 考虑下述线性规划问题:

运筹学教程 第一章习题解答 解:上界对应的模型如下(c,b取大,a取小) max Z=3x+6x2 -1x1+2x2≤12 st.3 2x1+4x2≤14 x1,x2≥0 最优值(上界)为:21 page 16 23 April 2025 School of Management
运筹学教程 School of Management page 16 23 April 2025 第一章习题解答 最优值(上界)为:21 + − + = + , 0 2 4 14 1 2 12 . max 3 6 1 2 1 2 1 2 1 2 x x x x x x st Z x x 解:上界对应的模型如下(c,b取大,a取小)