安徽大学：《运筹学》课程习题详解（PPT讲稿）第一章 线性规划

运筹学教程 第一章习题解答 min Z=2x-2x2 +3x3 -x1+x2+x3=4 (2) st -2x1+x2-x3≤6 x1≤0，x2≥0，x3无约束 maxZ=2x1+2x2-3x31+3x32 -x1+x2+x31-x32=4 St2x1+X2-x31+X32+x4=6 x1,x2,x31,x32x4≥0 page 7 23 April 2025 School of Management

运筹学教程 School of Management page 7 23 April 2025 第一章习题解答        − + −  − + + = = − + 1 2 3无约束 1 2 3 1 2 3 1 2 3 0, 0, 2 6 4 min 2 2 3 (2) x x x x x x x x x st Z x x x       + − + + = − + + − = = + − + , , , , 0 2 6 4 max 2 2 3 3 1 2 3 1 3 2 4 1 2 3 1 3 2 4 1 2 3 1 3 2 1 2 3 1 3 2 x x x x x x x x x x x x x x st Z x x x x

运筹学教程 第一章习题解答 1.3对下述线性规划问题找出所有基解，指出哪 些是基可行解，并确定最优解。 max Z=3x+x2+2x3 12x1+3x2+6x3+3x4=9 (①) 8x1+x2-4x3+2x=10 st 3x1-x6=0 x,≥0，)=1，.，6) minZ=5x1-2x2+3x3+2x4 X1+2x2+3x3+4x4=7 (2) st3 2x1+2x2+x3+2x4=3 x,≥0，(j=1,.4) page 8 23 April 2025 School of Management

运筹学教程 School of Management page 8 23 April 2025 第一章习题解答 1.3 对下述线性规划问题找出所有基解，指出哪 些是基可行解，并确定最优解。         = − = + − + = + + + = = + + 0（, 1, ,6） 3 0 8 4 2 10 12 3 6 3 9 max 3 2 (1) 1 6 1 2 3 5 1 2 3 4 1 2 3 x j  x x x x x x x x x x st Z x x x j       = + + + = + + + = = − + + 0,( 1, 4) 2 2 2 3 2 3 4 7 min 5 2 3 2 (2) 1 2 3 4 1 2 3 4 1 2 3 4 x j  x x x x x x x x st Z x x x x j

运筹学教程 第一章习题解答 max Z=3x+x2+2x3 12x1+3x2+6x3+3x4=9 (1) 8x1+x2-4x3+2x5=10 st< 3x1-x6=0 x,≥0，(j=1,.,6) 基可行解 X X2 Xg X4 X5 X6 Z 0 3 0 0 3.5 0 3 0 0 1.5 0 8 0 3 0 0 0 3 5 O 0.75 0 0 2 2.252.25 page 9 23 April 2025 School of Management

运筹学教程 School of Management page 9 23 April 2025 第一章习题解答         = − = + − + = + + + = = + + 0（, 1, ,6） 3 0 8 4 2 10 12 3 6 3 9 max 3 2 (1) 1 6 1 2 3 5 1 2 3 4 1 2 3 x j  x x x x x x x x x x st Z x x x j 基可行解 x1 x2 x3 x4 x5 x6 Z 0 3 0 0 3.5 0 3 0 0 1.5 0 8 0 3 0 0 0 3 5 0 0 0.75 0 0 0 2 2.25 2.25

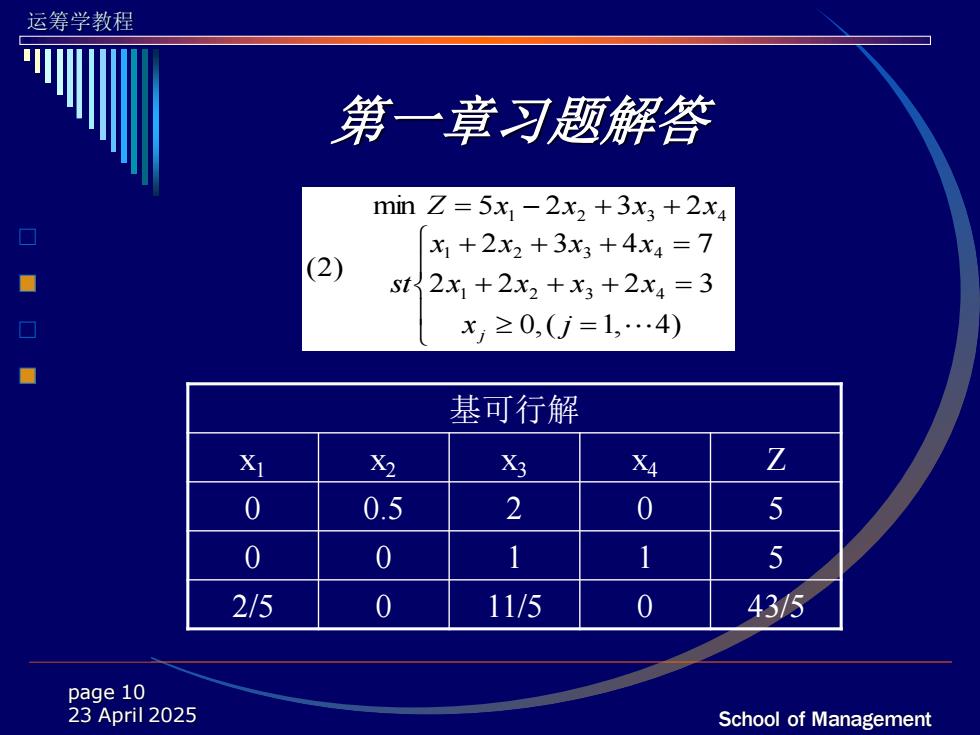
运筹学教程 第一章习题解答 min Z=5x1-2x2+3x3+2x4 x1+2x2+3x3+4x4=7 (2) st 2x1+2x2+x3+2x4=3 x,≥0，(j=1,.4) 基可行解 X X2 Xg XA Z 0 0.5 2 0 5 0 0 1 1 5 2/5 0 11/5 0 43/5 page 10 23 April 2025 School of Management

运筹学教程 School of Management page 10 23 April 2025 第一章习题解答       = + + + = + + + = = − + + 0,( 1, 4) 2 2 2 3 2 3 4 7 min 5 2 3 2 (2) 1 2 3 4 1 2 3 4 1 2 3 4 x j  x x x x x x x x st Z x x x x j 基可行解 x1 x2 x3 x4 Z 0 0.5 2 0 5 0 0 1 1 5 2/5 0 11/5 0 43/5

运筹学教程 第一章习题解答 1.4分别用图解法和单纯形法求解下述线性规划 问题，并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。 max Z=10x+5x2 3x1+4x2≤9 (1) st35x1+2x2≤8 x1,X2≥0 x2 (0,2.25) A 《1,1.5) x1 0,o)CB1.6,y page 11 23 April 2025 School of Management

运筹学教程 School of Management page 11 23 April 2025 第一章习题解答 1.4 分别用图解法和单纯形法求解下述线性规划 问题，并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。       +  +  = + , 0 5 2 8 3 4 9 . max 10 5 (1) 1 2 1 2 1 2 1 2 x x x x x x st Z x x