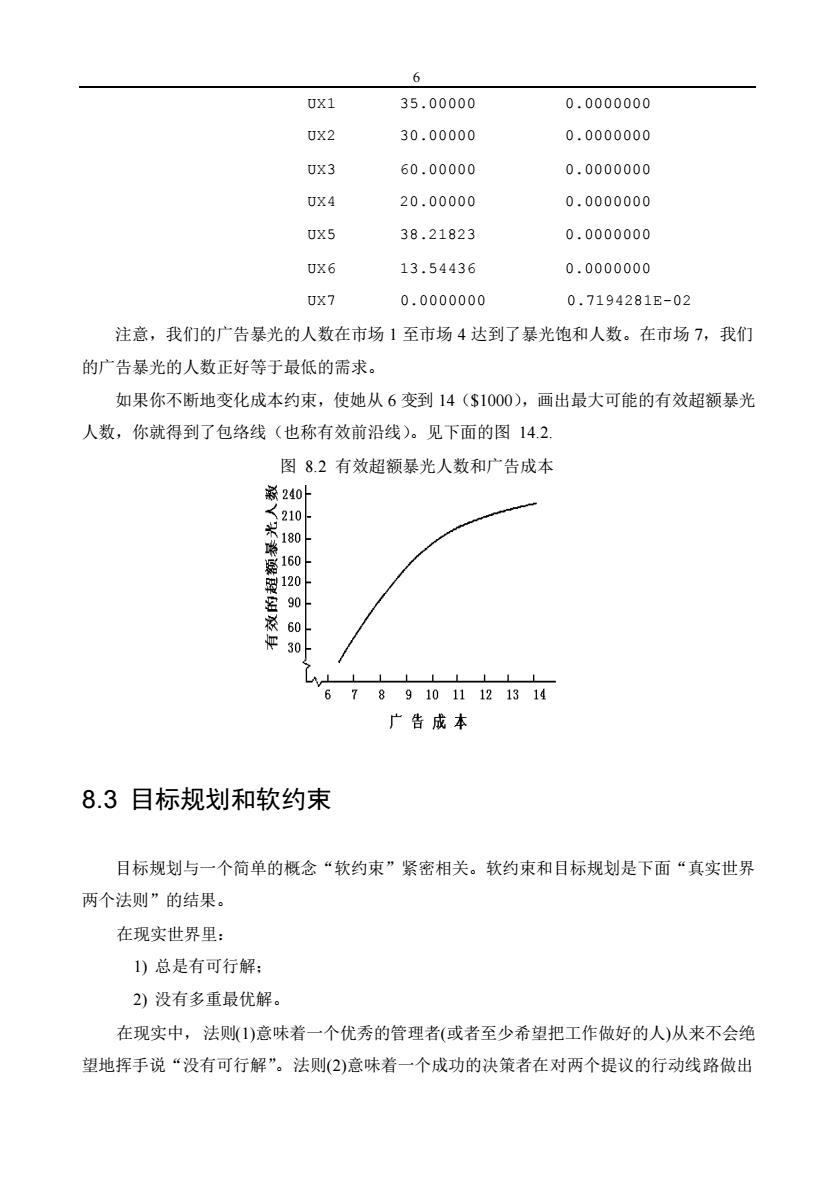
6 0X1 35.00000 0.0000000 UX2 30.00000 0.0000000 UX3 60.00000 0.0000000 0X4 20.00000 0.0000000 0X5 38.21823 0.0000000 UX6 13.54436 0.0000000 UX7 0.0000000 0.7194281E-02 注意,我们的广告暴光的人数在市场1至市场4达到了暴光饱和人数。在市场7,我们 的广告暴光的人数正好等于最低的需求。 如果你不断地变化成本约束,使她从6变到14($1000),画出最大可能的有效超额暴光 人数,你就得到了包络线(也称有效前沿线)。见下面的图14.2. 图8.2有效超额暴光人数和广告成本 亲240 210 180 60 67891011121314 广告成本 8.3目标规划和软约束 目标规划与一个简单的概念“软约束”紧密相关。软约束和目标规划是下面“真实世界 两个法则”的结果。 在现实世界里: 1)总是有可行解: 2)没有多重最优解。 在现实中,法则(1)意味着一个优秀的管理者(或者至少希望把工作做好的人)从来不会绝 望地挥手说“没有可行解”。法则(2)意味着一个成功的决策者在对两个提议的行动线路做出
6 UX1 35.00000 0.0000000 UX2 30.00000 0.0000000 UX3 60.00000 0.0000000 UX4 20.00000 0.0000000 UX5 38.21823 0.0000000 UX6 13.54436 0.0000000 UX7 0.0000000 0.7194281E-02 注意,我们的广告暴光的人数在市场 1 至市场 4 达到了暴光饱和人数。在市场 7,我们 的广告暴光的人数正好等于最低的需求。 如果你不断地变化成本约束,使她从 6 变到 14($1000),画出最大可能的有效超额暴光 人数,你就得到了包络线(也称有效前沿线)。见下面的图 14.2. 图 8.2 有效超额暴光人数和广告成本 8.3 目标规划和软约束 目标规划与一个简单的概念“软约束”紧密相关。软约束和目标规划是下面“真实世界 两个法则”的结果。 在现实世界里: 1) 总是有可行解; 2) 没有多重最优解。 在现实中,法则(1)意味着一个优秀的管理者(或者至少希望把工作做好的人)从来不会绝 望地挥手说“没有可行解”。法则(2)意味着一个成功的决策者在对两个提议的行动线路做出
选择时,总是有足够的标准区分出最好的行动线路。 通过前面的模型可知,这两个法则意味着一个好的模型应该:()总是有可行解:(b)没有 多重最优解。 8.3.1实例:多重最优解的第2个选择目标 下面介绍这个目标。我们使用的问题与第7章讨论的职员问题(7天/周)类似。变量: MT,W,RE,S,N分别表示在星期一、二、三、四、五、六、日每天开始雇佣的人数(每人 连续工作5天)。 MODEL: MIN=9*M+9*T+9*W+9*R+9*E+9*S+9*N; [MON] M +R+F+S+N >= 3: (TUE] M+T +F+S+N >= 3; [WED] M+T+W +S+N >= 8; [THU] M+T+W+R +N >= 8: (FRI] M+T+W+R+F >= 8: [SAT] T+W+R+F+S >= 3: [SUN] W+R+F+S+N >= 3; END 求解模型后可以得到下面的解答:, Global optimal solution found at step: 8 Obiective value: 72.00000 Variable Value Reduced Cost g 3.000000 0.000000 2.000000 0.000000 3.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 9.000000
7 选择时,总是有足够的标准区分出最好的行动线路。 通过前面的模型可知,这两个法则意味着一个好的模型应该:(a)总是有可行解;(b)没有 多重最优解。 8.3.1 实例:多重最优解的第 2 个选择目标 下面介绍这个目标。我们使用的问题与第 7 章讨论的职员问题(7 天/周)类似。变量: M, T, W, R, F, S, N 分别表示在星期一、二、三、四、五、六、日每天开始雇佣的人数(每人 连续工作 5 天)。 MODEL: MIN = 9*M + 9*T + 9*W + 9*R + 9*F + 9*S + 9*N; [MON] M + R + F + S + N >= 3; [TUE] M + T + F + S + N >= 3; [WED] M + T + W + S + N >= 8; [THU] M + T + W + R + N >= 8; [FRI] M + T + W + R + F >= 8; [SAT] T + W + R + F + S >= 3; [SUN] W + R + F + S + N >= 3; END 求解模型后可以得到下面的解答:. Global optimal solution found at step: 8 Objective value: 72.00000 Variable Value Reduced Cost M 3.000000 0.000000 T 2.000000 0.000000 W 3.000000 0.000000 R 0.000000 0.000000 F 0.000000 0.000000 S 0.000000 9.000000