厦门大学：《量子化学 Quantum Chemistry》课程电子教案（教学课件）Chapter 4 角动量与自旋 Angle momentum and spin

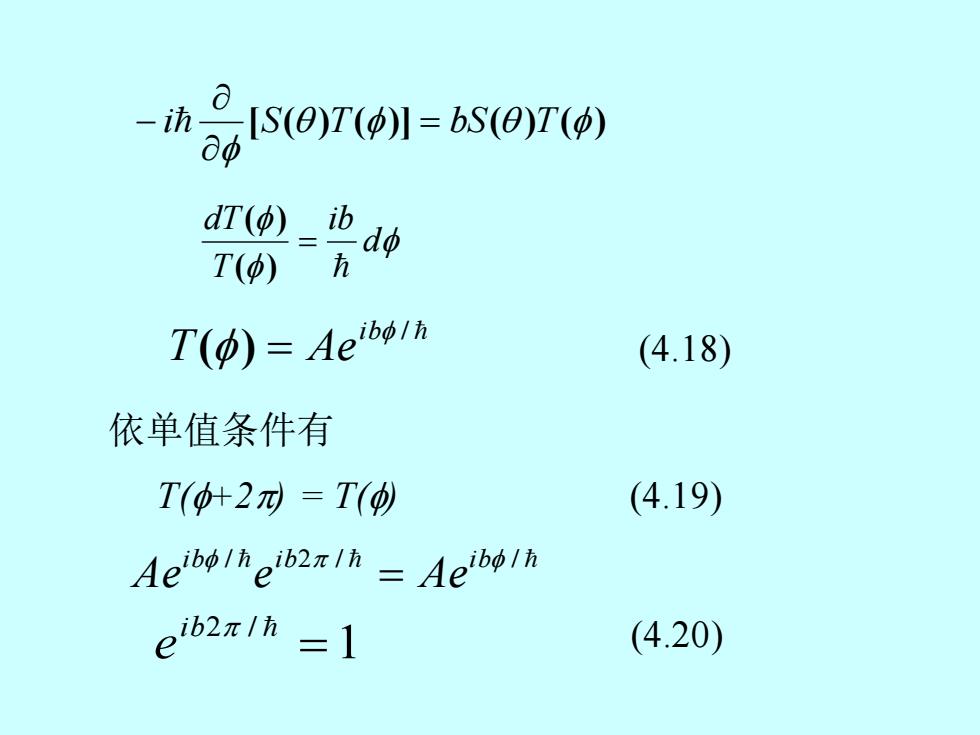
IS(0)T(p)1=bS(0)T(p) 88 d)ibd T()方 T()=Aeiboin (4.18) 依单值条件有 T(2=T( (4.19) Aebo1heb2π/h=Aebp1h eib2π1h =1 (4.20)

[ ( ) ()] ( ) ()  i S T = bS T   −     d ib T dT  = ( ) ( ) /  ( )   ib T = Ae (4.18) 依单值条件有 T(+2) = T() (4.19) i b /  i b  /  i b /  Ae e = Ae 2 1 2 = ib  /  e (4.20)

由，ea=cosa+iSin0a=1有u=2m m=0,±1，±2， 即 2πb/h=2um b=mh,m=0,±1，±2，. (4.21) (4.18)式可写成 T()=Aem0m=0,+1,+2,. (4.22) 角动量分量的本征值是量子化的

由 ， 有  = 2m m = 0, 1, 2, … = cos + sin  =1  e i i 即 2b/  = 2m b = m, m = 0,1,2,... (4.21) (4.18)式可写成   im T( ) = Ae m = 0, 1, 2, … (4.22) 角动量z分量的本征值是量子化的

F(r0.=R(r)Y(0=R(r)S(0 T( (4.23) 由归一化条件有 ipF(c,01r产sm6di0a=l (4.24) (4.23)代入(4.24)，得 0R1r2d1s(01sn6d91T(φ)0=1(4.25) 分别归一化 01R2(r川r2d=11s2(0)Isina0=11T2()地=1 (4.26)

令 F(r,,) = R(r) Y(,) = R(r) S() T() (4.23) 由归一化条件有 | F (r, , ) | r sin drd d 1 0 0 2 0 2 2      =       (4.24) (4.23) 代入(4.24)，得 | R (r) | r dr |S ( ) |sin d |T ( ) |d 1 0 0 2 0 2 2 2 2      =       (4.25) 分别归一化 1 0 2 2 =   | R (r)|r dr 1 0 2 =      | S ( )|sin d 1 2 0 2 =     | T ( ) |d (4.26)

T(=(Aeme )emed=d=1 1=云 \A2元 (4.27) T)=2元 m=0,±1，±2，. (4.28) 应用密级数方法解(4.17)角动量平方本征方 程，得

1 2 0 2 0 2 0 2    = = =      T  d Ae Ae d A A d i m i m | ( )| ( )* * 2 2 1 | A | = 2 1 | A|= (4.27)    im T e 2 1 ( ) = m = 0, 1, 2, … (4.28) 应用密级数方法解(4.17)角动量平方本征方 程,得：

本征值：c=方(k+|mD(k+|m|+l), k=0,1,2, (4.29) 角量子数：1=k+ml,m≤1 角动量（平方）： c=1(0+1)h2,1=0,1,2,3, (4.30) m=-1,-1+1,-1+2,,-1,0,1,2,3,,1 (4.31)

本征值： k = 0, 1, 2, … (4.29) ( | |)( | | 1), 2 c =  k+ m k+ m + 角量子数：l  k+|m|, |m| l 角动量(平方)： ，l=0,1, 2, 3, … (4.30) 2 c = l(l +1) m = -l, -l+1, -l+2, …, -1, 0, 1, 2, 3,…, l (4.31)