
Chapter 7 Electronic Structure of Diatomic Molecules 7.1 The Hydrogen Molecule Ion 1.Accurate solutions a 0 R b The H2*molecule.The nuclei are at a and b;R is the internuclear distance;roand ro are the distances from the the electron to nuclei a and 6 In the BO approximation,the Hamiltonian in atomic units is =-12-1-1+1 2 a店R Since the nuclei are fixed,1/R is a constant.The purely electronic Hamiltionian for H2can be rewritten as He1= 12 11 Ta Ih (7.1) Obviously,the Schroedinger equation is not separable in spherical polar coordinates.In 1927,Burrau showed that the separation of variables is possible using confocal elliptic coordinates.n.. g a The elliptic coordinates with two centers
Chapter 7 Electronic Structure of Diatomic Molecules 7.1 The Hydrogen Molecule Ion 1. Accurate solutions . . a b O R -e φ r ra rb The H2 + molecule. The nuclei are at a and b; R is the internuclear distance; ra and rb are the distances from the the electron to nuclei a and b. In the BO approximation, the Hamiltonian in atomic units is r r R H a b 1 1 1 2 1 2 = − ∇ − − + ∧ Since the nuclei are fixed, 1/R is a constant. The purely electronic Hamiltionian for H2 + can be rewritten as a b el r r H 1 1 2 1 2 = − ∇ − − ∧ (7.1) Obviously, the Schroedinger equation is not separable in spherical polar coordinates. In 1927, Burrau showed that the separation of variables is possible using confocal elliptic coordinates ξ,η,ϕ. . . a R b ra rb The elliptic coordinates with two centers ϕ

5=名+名 7=名6 R R (7.2) The ranges of these coordinates are: 0≤p≤2π,1≤5≤0,-1≤n≤1 (7.3) We have =2R(5+) 5=25-) (7.4) The H2*electronic Hamiltonian(7.1)in the elliptic coordinates has the form Hd=- 2 R2(E2-72) +2是+0-) -2 n 1102 2 2(7.5) -2&+g-11-7002RE+m)RE-》7 Hence the Schroedinger equation is HΨ(5,n,p)=EΨ(5,n,p) (7.6) Let Ψ(5,n,p)=L(5)M(n)Φ(p) (7.7) Substitution of(7.7)into the Schroedinger equation (7.6)leads to an equation in which the variables are separable d2 D(p)=-m2D(o) do" (7.8) m2 (g-224+25+,Rg-2L=079
R r r R r r a b a − b = + ξ = , η (7.2) The ranges of these coordinates are: 0 ≤ ϕ ≤ 2π , 1 ≤ ξ ≤ ∞, −1 ≤ η ≤ 1 (7.3) We have ( ) 2 1 ( ), 2 1 ra = R ξ +η rb = R ξ −η (7.4) The H2 + electronic Hamiltonian (7.1) in the elliptic coordinates has the form ( ) 2 ( ) 2 ) ] 1 1 1 1 2 ( [( 1) 2 (1 ) ( ) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 η ξ η ϕ ξ η ξ η η η η ξ ξ ξ ξ ξ η − − + − ∂ ∂ − + − + ∂ ∂ − ∂ ∂ + − ∂ ∂ + ∂ ∂ − − = − ∧ R R R Hel (7.5) Hence the Schroedinger equation is Ψ(ξ,η,ϕ) = Ψ(ξ,η,ϕ) ∧ el H el E (7.6) Let Ψ(ξ,η,ϕ) = L(ξ )M (η)Φ(ϕ) (7.7) Substitution of (7.7) into the Schroedinger equation (7.6) leads to an equation in which the variables are separable. ( ) ( ) 2 2 2 ϕ ϕ ϕ Φ = −m Φ d d (7.8) ) 0 2 1 1 ( 1) ' ' 2 ' ( 2 2 2 2 2 2 = − − + + + + − L m L L A R EelR ξ ξ ξ ξ ξ (7.9)

()M-2M-(4RM0 10 Solving the equation(7.8),we have (p)= V2π (7.11) where m=0,±l,+2,.. [1 when m=0 √2π (p)= -cosmo V2 when m 1,2... (7.12) √2 -sin mo The solution for M(n)is an infinite series of associated Legendre functions.L()also involves an infinite series.The requirement that the wave function be well behaved leads to the conclusion that for a fixed value of R,only certain values of Ee are allowed (i.e.discrete);this gives a series of electronic states,corresponding electronic energy E(R)=E+ R (7.13) The electronic energies must be calculated numerically.The series of energy levels are marked by quantum numbers n,I,and m,whose allowed values are n=1,2,3,… l≤n-1 (7.14) m≤I 10,1,2,3,… s,p,d,f
) 0 2 1 1 (1 ) ' ' 2 ' ( 2 2 2 2 2 = − − − − + + M m M M A EelR η η η η (7.10) Solving the equation (7.8), we have ϕ π ϕ im e 2 1 Φ( ) = (7.11) where m = 0, ±1, ±2, … or = Φ = ϕ π ϕ π π ϕ m m when m sin 2 1 cos 2 1 0 2 1 ( ) when m = 1, 2, … (7.12) The solution for M(η) is an infinite series of associated Legendre functions. L(ξ) also involves an infinite series. The requirement that the wave function be well behaved leads to the conclusion that for a fixed value of R, only certain values of Eel are allowed (i.e. discrete); this gives a series of electronic states, corresponding electronic energy R E R Eel 1 ( ) = + (7.13) The electronic energies must be calculated numerically. The series of energy levels are marked by quantum numbers n, l, and m, whose allowed values are m l l n n ≤ ≤ − = 1 1, 2, 3, " (7.14) l 0, 1, 2, 3, … s, p, d, f. …
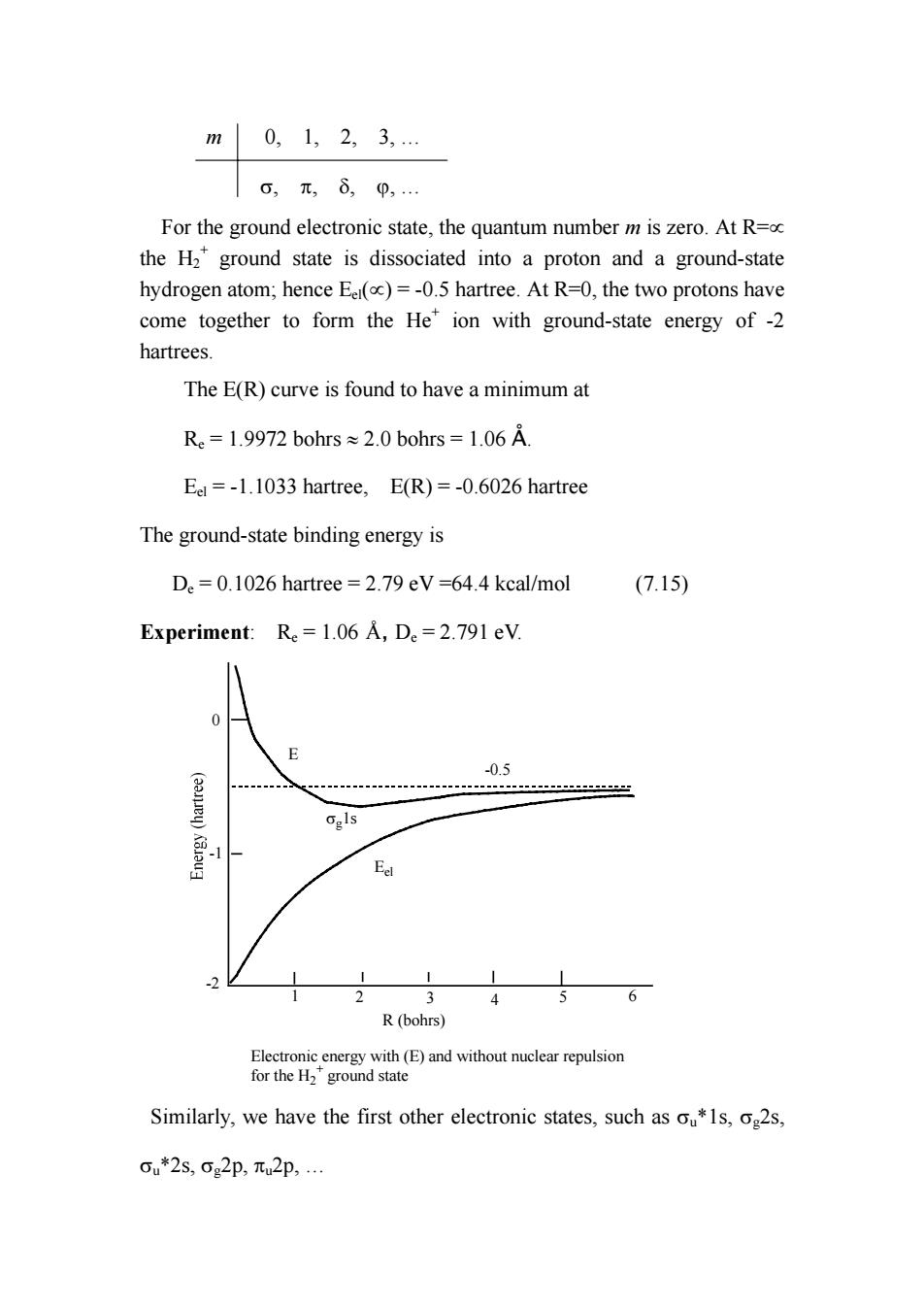
m0,1,2,3, o,元,80,… For the ground electronic state,the quantum number m is zero.At R= the H2*ground state is dissociated into a proton and a ground-state hydrogen atom;hence Eer(oc)=-0.5 hartree.At R=0,the two protons have come together to form the He*ion with ground-state energy of-2 hartrees. The E(R)curve is found to have a minimum at Re=1.9972 bohrs 2.0 bohrs 1.06 A. Eel=-1.1033 hartree,E(R)=-0.6026 hartree The ground-state binding energy is D.=0.1026 hartree =2.79 eV=64.4 kcal/mol (7.15) Experiment:Re=1.06 A,De=2.791 eV. 0.5 Ggls E 3 456 R(bohrs) Electronic energy with(E)and without nuclear repulsion for the H2 ground state Similarly,we have the first other electronic states,such as s,o2s. ou*2s,cg2p,元u2p
m 0, 1, 2, 3, … σ, π, δ, ϕ, … For the ground electronic state, the quantum number m is zero. At R=∝ the H2 + ground state is dissociated into a proton and a ground-state hydrogen atom; hence Eel(∝) = -0.5 hartree. At R=0, the two protons have come together to form the He+ ion with ground-state energy of -2 hartrees. The E(R) curve is found to have a minimum at Re = 1.9972 bohrs ≈ 2.0 bohrs = 1.06 Å. Eel = -1.1033 hartree, E(R) = -0.6026 hartree The ground-state binding energy is De = 0.1026 hartree = 2.79 eV =64.4 kcal/mol (7.15) Experiment: Re = 1.06 Å, De = 2.791 eV. 0 -1 -2 R (bohrs) 1 2 3 4 5 6 Eel E Electronic energy with (E) and without nuclear repulsion for the H2 + ground state σg1s -0.5 Similarly, we have the first other electronic states, such as σu*1s, σg2s, σu*2s, σg2p, πu2p, …

2.Approximate Treatment of the H2" Trial function: Consider a limiting behavior of the H2*ground-state electronic wave function as R approaches p=CalSa +CplSp (7.16) -e-n When R goes zero,we get the He'ion,which has the ground-state wave function(Z=2) 2 1\π (7.17) Note that at the R=0the trial function(7.16)goes to (G+c2) e V Comparing with (7.17),we see that (7.16)has the wrong limiting behavior at R =0.We can fix things by multiplying ra and ro in the exponentials by a variational parameter k=k(R).For correct limiting behavior at zero and infinite internuclear distance,we have K(0)=2,k(oc)=1 We thus take as the trial function 0=Ca功sa+C691sb (7.18) where k 4π -e-kn (7.19)
2. Approximate Treatment of the H2 + Trial function: Consider a limiting behavior of the H2 + ground-state electronic wave function as R approaches ∝. a a b b ϕ = c 1s + c 1s (7.16) a br b r a s e s e − − = = π π 1 , 1 1 1 When R goes zero, we get the He+ ion, which has the ground-state wave function (Z=2) r e 2 3 2 − π (7.17) Note that at the R = 0 the trial function (7.16) goes to r c c e− + π 1 ( ) 1 2 . Comparing with (7.17), we see that (7.16) has the wrong limiting behavior at R = 0. We can fix things by multiplying ra and rb in the exponentials by a variational parameter k = k(R). For correct limiting behavior at zero and infinite internuclear distance, we have K(0) = 2, k(∝) =1 We thus take as the trial function a sa b sb c c ϕ = φ1 + φ 1 (7.18) where a b kr sb kr sa e k e k − − = = π φ π φ 3 1 3 1 , (7.19)