
Chapter 2 Atomic Structure
Chapter 2 Atomic Structure
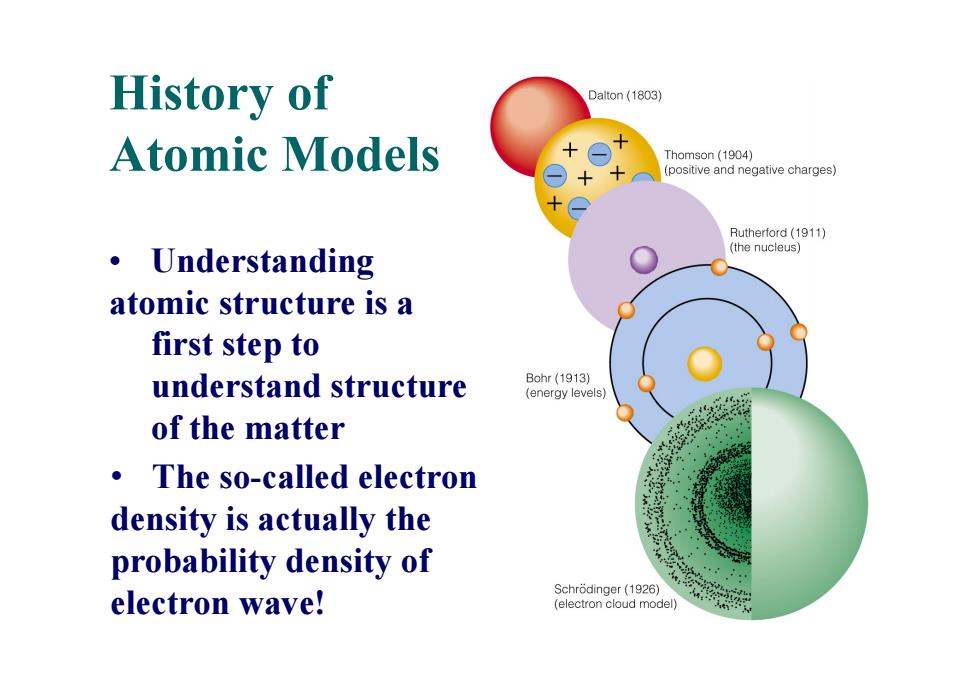
History of Dalton (1803) Atomic Models Thomson(1904) (positive and negative charges) Rutherford(1911) Understanding (the nucleus) 。 atomic structure is a first step to understand structure Bohr(1913) (energy levels) of the matter The so-called electron density is actually the probability density of Schrodinger(1926) electron wave! (electron cloud model)
History of Atomic Models • Understanding atomic structure is a first step to understand structure of the matter • The so-called electron density is actually the probability density of electron wave!

2.1 The Schrodinger equation and its solution for one-electron atoms 2.1.1 The Schrodinger equation The Hamiltonian Operator of one-electron atoms H atom,Het and Li2+ 月=i+元+。= 2mn V2+V-e e The reduced mass u= M·me 1836m。 ≈0.999m。 M+me (1+1836)m
2.1 The Schrödinger equation and its solution for one-electron atoms 2.1.1 The Schrödinger equation The Hamiltonian Operator of one-electron atoms H atom, He + and Li2+ e n e e n n n e n e V m m H T T V ˆ 2 2 ˆ ˆ ˆ ˆ 2 2 2 2 1836 0.999 (1 1836) e e e e e Mm m m Mm m The reduced mass e n

Consider that the electron approximately surrounds the atomic nucleus,the Hamilton operator can be simplified as 、 +n 2m。 = 方2 2 2m。x+ n-e Ze2 e n-e 4π8o' r=vx2+y2+22 The Schrodinger equation Hy =Ew Separation of variables
e n e e e n e V m H T V ˆ 2 ˆ ˆ ˆ 2 2 r Ze Vn e 0 2 4 ˆ Consider that the electron approximately surrounds the atomic nucleus, the Hamilton operator can be simplified as r e 2 2 2 r x y z 2 n-e 2 2 2 2 2 e 2 V ˆ ) x y z ( 2m H - ˆ Separation of variables ? The Schrödinger equation Hˆ E
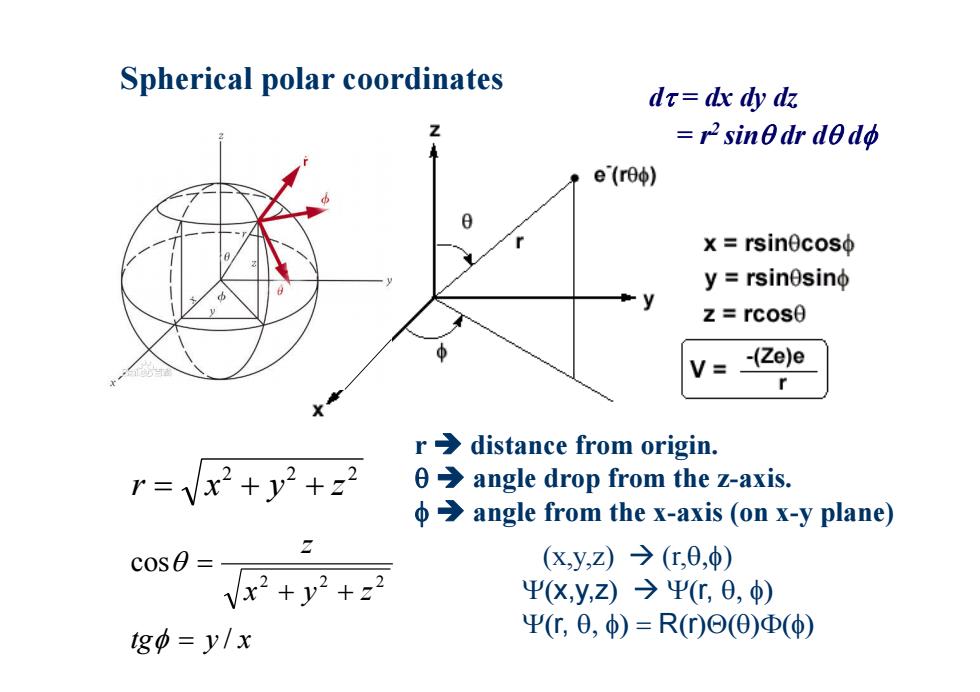
Spherical polar coordinates dr-dx dy dz Z r2 sin0dr dedo e(reo) X=rsinθcoso y=rsinθsino z=rcosθ V= -(Ze)e X r>distance from origin. r=vx2+y2+22 0>angle drop from the z-axis. φ→angle from the x-axis(onx-y plane) c0s0= (xy,z)→(c,0,φ) Vx2+y2+22 Ψ(X,y,Z)→ΨC,0,) tgo=y/x Ψ,0,φ)=R(0)⊙(0)Φ(φ)
Spherical polar coordinates 2 2 2 r x y z (x,y,z) (r, ) x,y,z r, r, R r r distance from origin. angle drop from the z-axis. angle from the x-axis (on x-y plane) 2 2 2 cos x y z z tg y / x d = dx dy dz = r2 sin dr d d