Introduction 1.对称性是物理体系、化学体系的普遍性质之一 对不同形式的体系,对称性具有不同的内涵 2.应用对称性原理可以建立体系状态性质与其特定对称 性质的关联,使问题的研究得以简化 Example1CH4电子结构 8个价电子分为两组:~14eV(6个电子);~23eV(2个电子) HΨ=EΨ Ta点群 月=-+ C CH, 4H =3 2a 2++↓ 对称化的MOs 2p+++ 十十+十 ↓ 2x1 扑扑扑Ps:V) 1.3 1.5 1.8 2.1 24 Ionization energy MJ.mol a.2 UrS:210) A0s(C:2s,2p,/2p,2p;4H:41s)
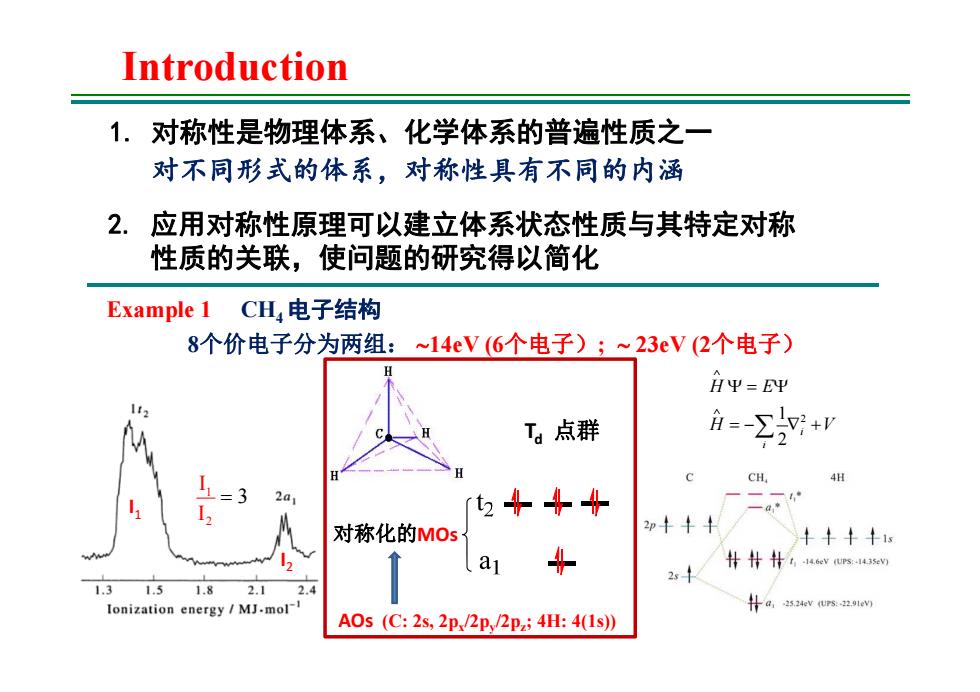
Introduction 1. 对称性是物理体系、化学体系的普遍性质之一 对不同形式的体系,对称性具有不同的内涵 2. 应用对称性原理可以建立体系状态性质与其特定对称 性质的关联,使问题的研究得以简化 Example 1 CH4 电子结构 8个价电子分为两组: 14eV (6个电子); 23eV (2个电子) I1 I2 1 2 I I 3 Td 点群 AOs (C: 2s, 2px/2py/2pz; 4H: 4(1s)) 对称化的MOs H V H E i i 2 2 1
Example2球对称场中Ym(e,中)的性质(形式) V(r)→球对称场 e(r06) dr=dx dy dz =r2sinedr dedo x'yizk x=rsinecos 1=i+j+ki方k为整数 y=rsinesino z=rcos0 对给定的,可能的次函数集合构成其不变 V=(Ze)e 的子空间 r i=j=1,k=0 ¥,dy i=k=1,j=0 ,d 1=0,i=j=k=0, 1,s jk=1,i=0 ,dz 1=2,i+j+k=2 r i=1,j=k=0 Px i=2,jk=0 j2,i=k=0 1=1,i+j+k=1- j1,ik=0¥,py Lk=2,i=j=0 k=1,ij=0,P2 x2-y ,z2 在球对称场中(原子体系) 3r2-2 5个d轨道是简并的 d
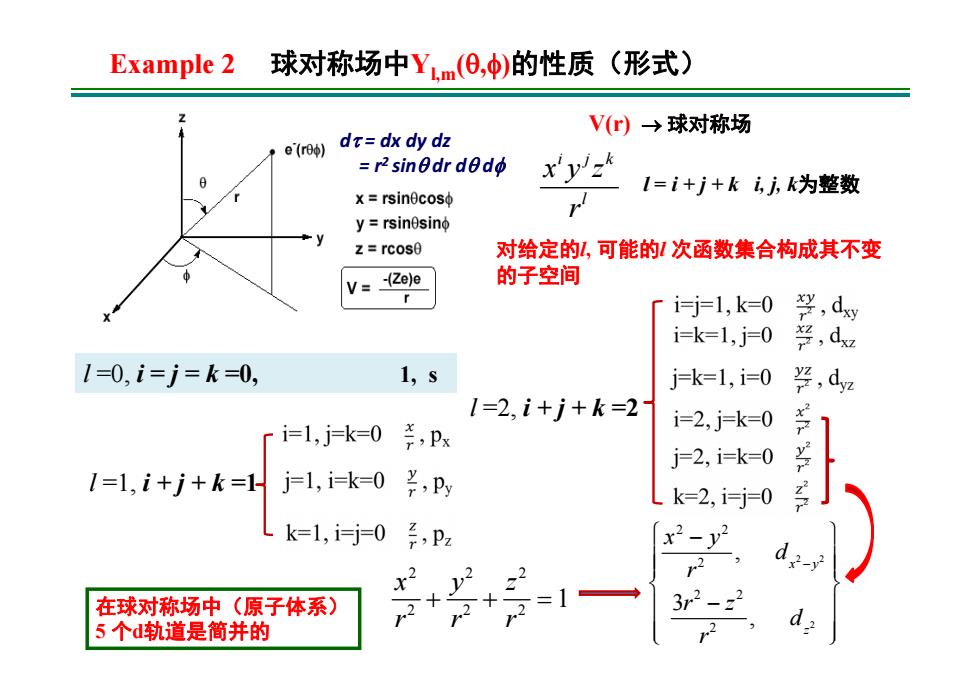
Example 2 球对称场中Yl,m(,)的性质(形式) i jk l x y z r V(r) 球对称场 l = i + j + k i, j, k为整数 对给定的l, 可能的l 次函数集合构成其不变 的子空间 l =1, i + j + k =1 l =0, i = j = k =0, 1, s l =2, i + j + k =2 2 22 222 1 xyz rrr 2 2 2 2 2 2 2 2 2 , 3 , x y z x y d r r z d r 在球对称场中(原子体系) 5 个d轨道是简并的 d = dx dy dz = r2 sin dr d d
低对称性下简并轨道能级的分裂 八面体场(0/0) 在八面体群操作下不变 dy de,d a-,d} 进一步降低对称性→C4轴拉长 C4X。→y C3消失,轨道分组: {dw,de,d}→{d,d} dy ad}-a月 {d} dy d 0& d ag 炉为 be 是的 g dd eg 0 Dab/Cab
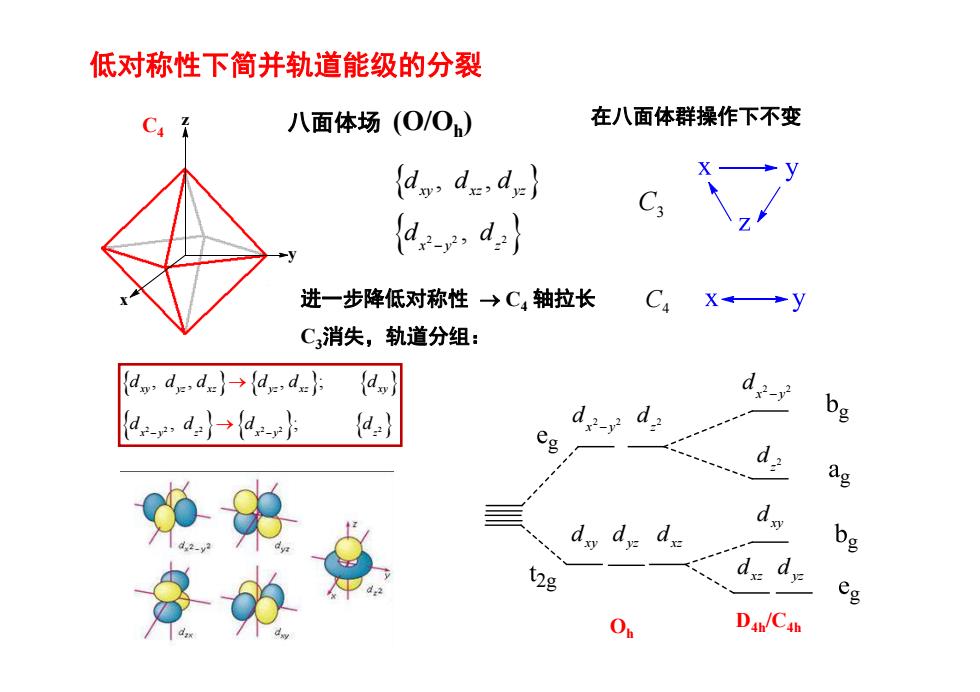
低对称性下简并轨道能级的分裂 22 2 , , , xy xz yz xy z d dd d d 进一步降低对称性 C 4 轴拉长 C 3消失,轨道分组: 八面体场 (O/O h ) C3 C4 x y C z 在八面体群操作下不变 4 22 2 22 2 , , , ; , ; xy yz xz yz xz xy xy z xy z d dd dd d dd d d g 2g g g g g 22 2 x y z d d xz yz d d 2 2 x y d 2z d xy d xy yz xz dd d O h D4h/C4h
dx2y2 big dz2 dx2-y2 eg t29 d22 a1g t2 6Dq d网p29 dxy 4Dq b2g -e dz2 dx2-y2 dz2 _a1g eg dyz dxz eg 立方体场 四面体场 球形场 八面体场四方畸变 平面四方场 Ou Ta On Dah Dah
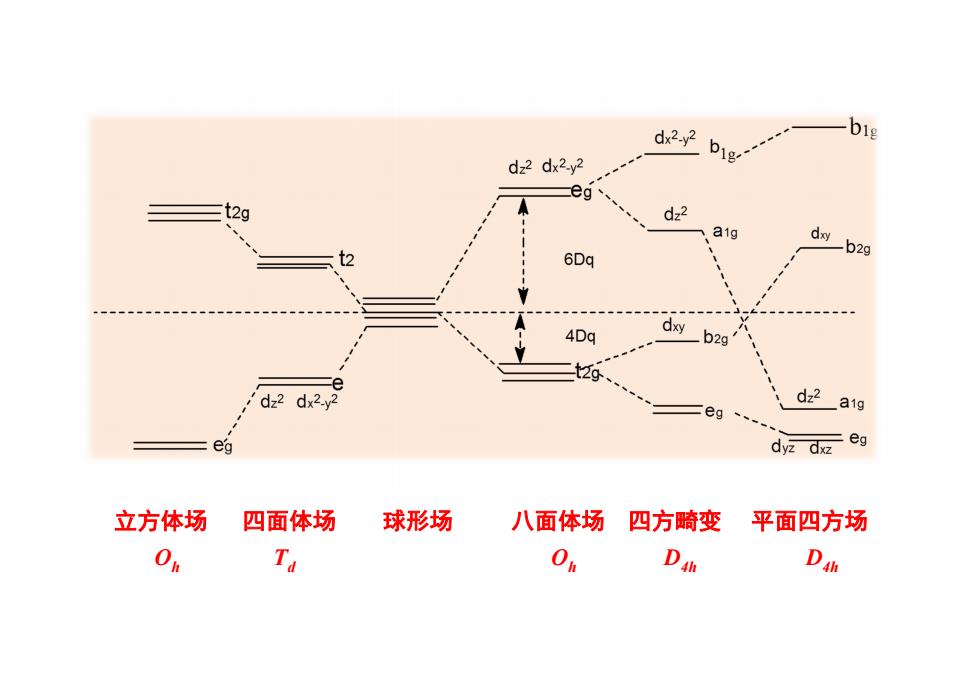
立方体场 四面体场 球形场 八面体场 四方畸变 平面四方场 O h Td O h D4h D4h
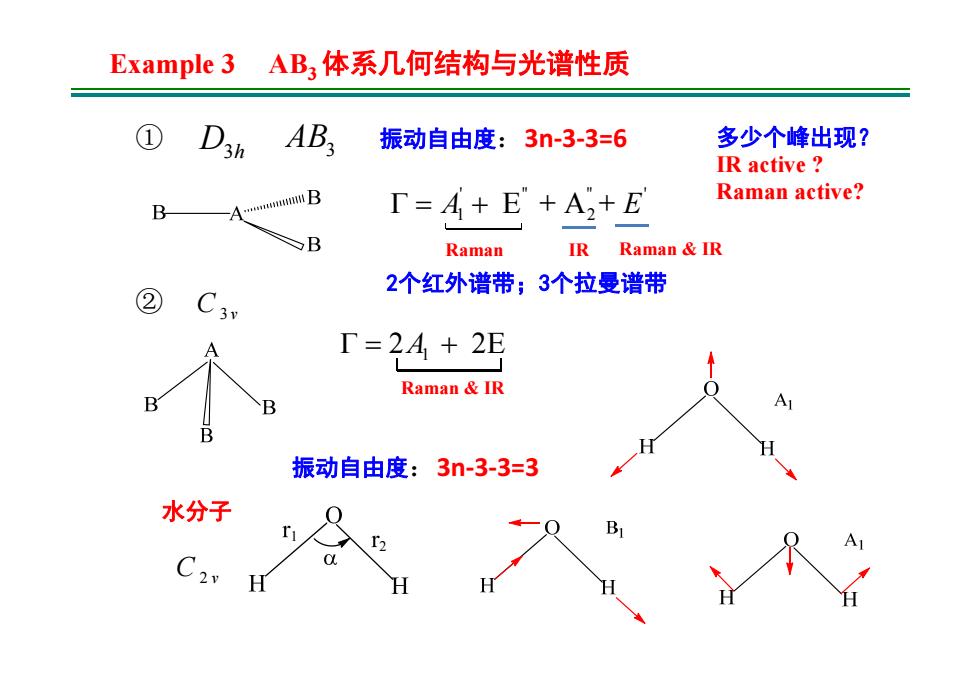
Example3AB,体系几何结构与光谱性质 ① D3h AB. 振动自由度:3n-3-3=6 多少个峰出现? IR active Raman active? B B T=4+E+A,+E ✉B Raman IR Raman IR 2个红外谱带;3个拉曼谱带 2 C3 Γ=2A+2E Raman IR 振动自由度:3n-3-3=3 水分子
多少个峰出现? IR active ? Raman active? C3 v ① AB3 ' " "' A1 2 E + A + E ② D3h 振动自由度:3n‐3‐3=6 Raman Example 3 AB3 体系几何结构与光谱性质 IR Raman & IR 2个红外谱带;3个拉曼谱带 1 2 2E A Raman & IR C 2 v 1 2 振动自由度:3n‐3‐3=3 水分子