
第一章光的干涉 §1一1光的电磁理论 十九世纪七十年代,麦克斯韦发展了电磁理论,从而导致电磁波的发现。电磁波在不同 介质的界面上发生反射和折射现象,在传播中出现干涉、衍射和偏振现象,而根据当时已有 的知识,光波也具有完全相似的干涉、衍射和偏振等现象,它们之间有什么联系呢?电磁波 在真空中的速度 在实验误差范围以内,这个常数c与己测得的光速相等。于是麦克斯韦得出这样的理论:光 是某一波段的电磁波,©就是光在真空中的传播速度。 介质中电磁波的速度为 折射率n=9 则n=VE,4, E和户都垂直ū,电磁波是横波。维纳实验证明,对人的眼睛或感光仪器起作用的是 电场强度E,所以光波中的振动矢最是指电场强度E。 电磁波中能为人眼所感受的波长在3900A-7600A之间,对应的频率范围7.5×10~4.1 ×10Hz。 人眼的视网膜或物理仪器所检测到的光的强弱都是由能流密度的大小来决定的(单位 时间内通过与波的传播方向垂直的单位面积的能量。).任何波动所传递的能流密度与振幅的 平方成正比,所以,光的强度或光照度(即平均能流密度)为 1xA(A为电场强度) 在波动光学中,主要是讨论光波所到之处的相对光照度。因而通常只需计算光波在各 处的振幅的平方值,而不需要计算各处的光照度的绝对值
第一章 光的干涉 §1—1 光的电磁理论 十九世纪七十年代,麦克斯韦发展了电磁理论,从而导致电磁波的发现。电磁波在不同 介质的界面上发生反射和折射现象,在传播中出现干涉、衍射和偏振现象,而根据当时已有 的知识,光波也具有完全相似的干涉、衍射和偏振等现象,它们之间有什么联系呢?电磁波 在真空中的速度 0 0 1 c 在实验误差范围以内,这个常数 c 与已测得的光速相等。于是麦克斯韦得出这样的理论:光 是某一波段的电磁波,c 就是光在真空中的传播速度。 介质中电磁波的速度为 r r c u 折射率 u c n 则 r r n E 和 H 都垂直u ,电磁波是横波。维纳实验证明,对人的眼睛或感光仪器起作用的是 电场强度 E ,所以光波中的振动矢量是指电场强度 E 。 电磁波中能为人眼所感受的波长在 3900Å~7600Å 之间,对应的频率范围 7.5×1014~4.1 ×1014Hz。 人眼的视网膜或物理仪器所检测到的光的强弱都是由能流密度的大小来决定的(单位 时间内通过与波的传播方向垂直的单位面积的能量。)。任何波动所传递的能流密度与振幅的 平方成正比,所以,光的强度或光照度(即平均能流密度)为 2 I A (A 为电场强度) 在波动光学中,主要是讨论光波所到之处的相对光照度。因而通常只需计算光波在各 处的振幅的平方值,而不需要计算各处的光照度的绝对值

§1一2波动的独立性、叠加性。简谐波的表达式 一、机械波的独立性和叠加性 在机械振动和机械波中我们已注意到从几个振源发出的波相遇于同一区域时,只要振 动不十分强烈,就可以保持自己的特性(频率、振幅和振动方向等),按照自己原来的传播 方向继续前进,彼此不受影响。这就是波动独立性的表现。 在相遇区域内,介质中一点的合位移是各波单独传播时在该点所引起的位移的矢量和, 因此,可以简单的,没有任何畸变地把各波的分位移按照矢最加法叠加起来,这就是波动的 叠加性。这种叠加性是以独立性为条件的,是最简单的叠加。 通常情况下,波动方程是线性微分方程,简谐波的表达式就是它的一个解。如果有两 个独立的函数都能满足同一个给定的微分方程,那么这两个函数的和也必然是这个微分方程 的解。这就是两个具有独立性的波的叠加的数学意义。 二、光波的描述 (1)光波的几荷描述:波动是振动在空间的传播,波动所存在的空间称为波场,波场 中每点的物理状态随时间作周期性变化,而在每一瞬时波场中各点物理状态的空间分布也呈 现一定的周期性,通常把某一时刻振动相位相同各点的轨迹称为波面,把能量传播的路径称 为波线。在各向同性的介质中,波线与波面处处正交。 (2)光波的描述 任一理想的单色光场可用下述的波动表达式描述 E(F,t)=A(F)coslot-p()] 4(F)给出了光场中的振幅分布,()是各点相位比原点落后的值,它确定了光场中相 位的相对分布。只要给定光场的振幅分布和相位分布,则该频率的单色光场就完全确定了。 上式的复数表达式可写为 E(F,t)=A(F)eo =A(F)costot-o(F)]-iA(F)sin[ot-p()] 其实部就是单色光场的波动表达式 E(F,1)=A(F)ee =E(F)ew E()称为复振幅。包含了我们感兴趣的信息。其模量A)代表振幅在空间的分布, 其辐角(F)代表相位的空间的分布。只要给定光场的复振幅,则该频率的单色光场就完全 确定了
§1—2 波动的独立性、叠加性。简谐波的表达式 一、机械波的独立性和叠加性 在机械振动和机械波中我们已注意到从几个振源发出的波相遇于同一区域时,只要振 动不十分强烈,就可以保持自己的特性(频率、振幅和振动方向等),按照自己原来的传播 方向继续前进,彼此不受影响。这就是波动独立性的表现。 在相遇区域内,介质中一点的合位移是各波单独传播时在该点所引起的位移的矢量和, 因此,可以简单的,没有任何畸变地把各波的分位移按照矢量加法叠加起来,这就是波动的 叠加性。这种叠加性是以独立性为条件的,是最简单的叠加。 通常情况下,波动方程是线性微分方程,简谐波的表达式就是它的一个解。如果有两 个独立的函数都能满足同一个给定的微分方程,那么这两个函数的和也必然是这个微分方程 的解。这就是两个具有独立性的波的叠加的数学意义。 二、光波的描述 (1)光波的几荷描述:波动是振动在空间的传播,波动所存在的空间称为波场,波场 中每点的物理状态随时间作周期性变化,而在每一瞬时波场中各点物理状态的空间分布也呈 现一定的周期性,通常把某一时刻振动相位相同各点的轨迹称为波面,把能量传播的路径称 为波线。在各向同性的介质中,波线与波面处处正交。 (2)光波的描述 任一理想的单色光场可用下述的波动表达式描述 E(r,t) A(r) cos t (r) A(r) 给出了光场中的振幅分布, (r) 是各点相位比原点落后的值,它确定了光场中相 位的相对分布。只要给定光场的振幅分布和相位分布,则该频率的单色光场就完全确定了。 上式的复数表达式可写为 ( ) ( , ) ( ) ~ i t r E r t A r e A(r) cos t (r) iA(r)sin t (r) 其实部就是单色光场的波动表达式 i r i t i t E r t A r e e E r e ( ) ~ ( , ) ( ) ~ ( ) ( ) ~ E r 称为复振幅。包含了我们感兴趣的信息。其模量 A(r) 代表振幅在空间的分布, 其辐角 (r) 代表相位的空间的分布。只要给定光场的复振幅,则该频率的单色光场就完全 确定了

对于单色平面波E(F,)=Acos(om-k·F+”,) E(F)=Aeir) 对于单色发散球面波5G,)=4c0s01-:+,) E(F)=toene-n) 光强的复振幅表示为(F)=A(F)=E()E() 三、光波的相干与不相干叠加 设有两列光波分别从点光源s和s发出,经过元和万传播到空间任一点P。 S 图1-1光波的叠加 光源处:A。c0s(@,1+po1) 4o cos(o,f+pm) 挞P点C,0=4coa-受+ om =4 cosotk+on E2(F.1)=A2 cos(@2tk+o2) 如果E和E2同向,则1时刻P点的光矢量为 E)=EG,)+E,(G,)
对于单色平面波 ( , ) cos( ) 0 E r t A t k r ( ) 0 ( ) ~ i k r E r Ae 对于单色发散球面波 ( , ) cos( ) 0 0 t kr r A E r t 0 ( ) 0 ( ) ~ i kr e r A E r 光强的复振幅表示为 ( ) ~ ( ) ~ ( ) ( ) 2 I r A r E r E r 三、光波的相干与不相干叠加 设有两列光波分别从点光源 s1 和 s2发出,经过 1r 和 2r 传播到空间任一点 P。 图 1-1 光波的叠加 光源处: cos( ) 10 1 01 A t cos( ) 20 2 02 A t 到达 P 点: 01 1 1 1 1 1 1 ( , ) cos ( ) u r E r t A t 1 1 1 1 01 01 1 1 1 1 1 cos 2 cos A t k r T u r A t ( , ) cos( ) 2 2 2 2 2 2 02 E r t A t k r 如果 E1 和 E2 同向,则 t 时刻 P 点的光矢量为 ( ) ( , ) ( , ) 1 2 2 E t E r t E r t

E(1)=A cos(@-k+o)+A cos(@t-k+o) 如果o,同2相同 E(1)=A cos(@t-k+o)+A2 cos(@1-k +o) Acos(or+p) A2=A+A+2A,4,cos(p2-9) 如法器 1=1+2+2h2cosp2-9) 实际观察到的总是在较长时间内的平均强度,在某一时间间隔?内,合振动的平均相对 强度为 7=L4++244osg,-9 cotp.d 如p2-g,同时间无关 1=1+12+2Vcos(p2-m) 02-9=2k元 k=0,1,2 1=1,+12+2最大 p:-9=(2k+1)r j=0,12, 1=12+1-2山2最小 这种现象称为干涉现象,2、,石2c0s(p,一9,)称为干涉项。 「振动方向相同 从上面的讨论看出,干涉条件为 频率相同 位相差恒定 称为相干条件。满足相干条件的两束光称为相干光。 着-%随时间面变,则co0g,-A:=0 则1=1+12
( ) cos( ) cos( ) 1 1 1 1 01 2 2 2 2 02 E t A t k r A t k r 如果1 同 2 相同 cos( ) ( ) cos( ) cos( ) 1 1 1 1 01 2 2 2 2 02 A t E t A t k r A t k r 2 cos( ) cos cos sin sin 2 cos( ) 1 2 1 2 2 1 2 1 2 2 1 1 2 2 1 2 2 1 2 2 2 1 2 I I I I I A A A A tg A A A A A 实际观察到的总是在较长时间内的平均强度,在某一时间间隔 内,合振动的平均相对 强度为 0 1 2 1 2 2 1 0 1 2 2 1 2 2 2 1 cos( ) 1 2 2 cos( ) 1 I I I I dt I A A A A dt 如 2 1 同时间无关 2 cos( ) 1 2 1 2 2 1 I I I I I 2 1 2k k 0,1,2 1 2 1 2 I I I 2 I I 最大 2 1 (2k 1) j 0,1,2, 2 1 1 2 I I I 2 I I 最小 这种现象称为干涉现象, 2 cos( ) 1 2 2 1 I I 称为干涉项。 从上面的讨论看出,干涉条件为 位相差恒定 频率相同 振动方向相同 称为相干条件。满足相干条件的两束光称为相干光。 若 2 1 随时间而变,则 0 2 1 1 cos( ) 0 1 d 则 1 2 I I I
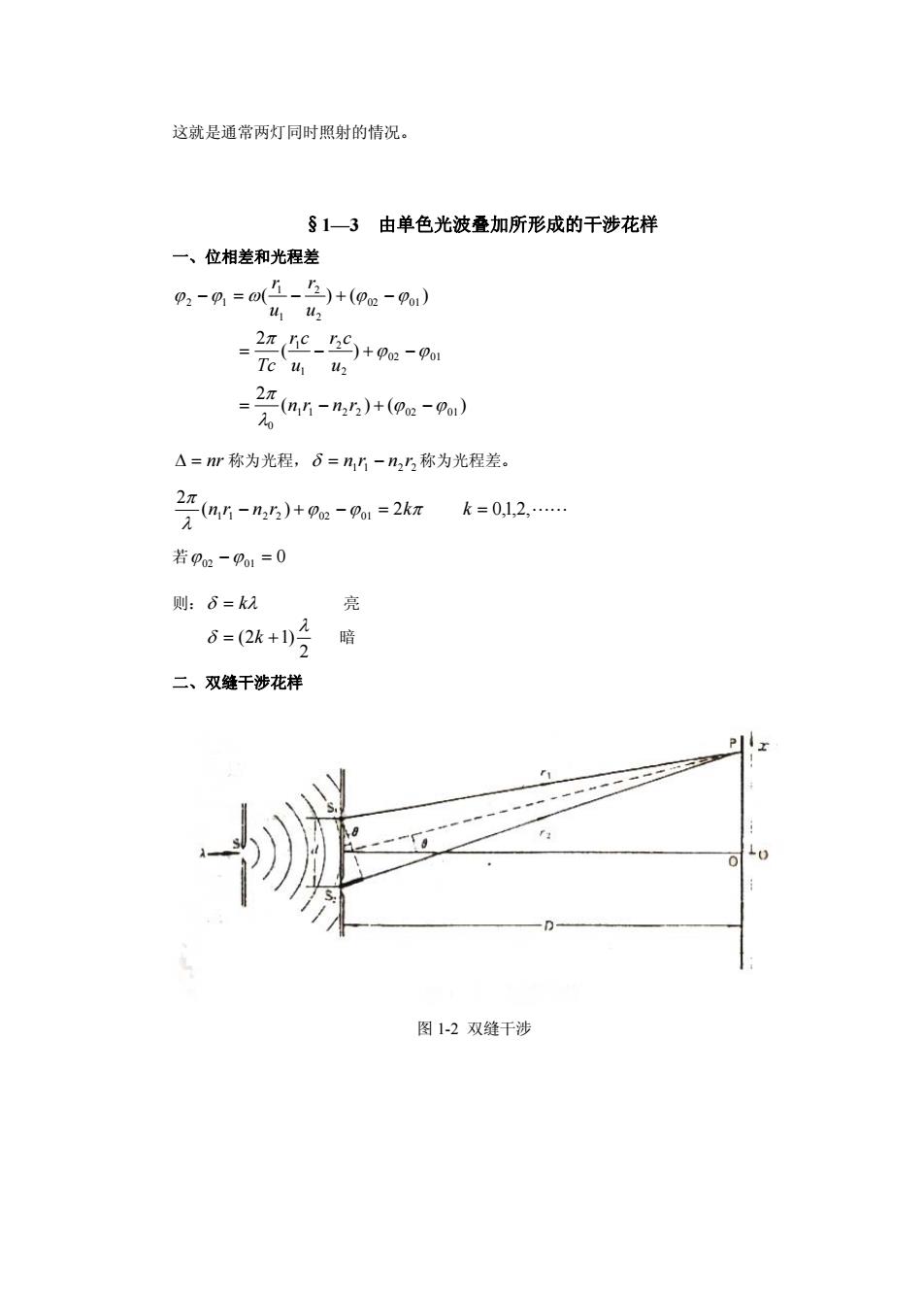
这就是通常两灯同时照射的情况。 §1一3由单色光波叠加所形成的干涉花样 一、位相差和光程差 %-g=o哈-受+e-) =2票华-5+8-n Te442 △=m称为光程,6=n,-n,称为光程差 2(a5-m,n)+m-pm=2 k=0,1,2, 若p2-po1=0 则:6=k2 6=(2k+)号暗 二、双缝干涉花样 P 图1-2双缝干涉
这就是通常两灯同时照射的情况。 §1—3 由单色光波叠加所形成的干涉花样 一、位相差和光程差 ( ) ( ) 2 ( ) 2 ( ) ( ) 1 1 2 2 02 01 0 02 01 2 2 1 1 02 01 2 2 1 1 2 1 n r n r u r c u r c Tc u r u r nr 称为光程, 1 1 2 2 n r n r 称为光程差。 ( ) 2 0,1,2, 2 n1r1 n2 r2 02 01 k k 若02 01 0 则: k 亮 2 (2 1) k 暗 二、双缝干涉花样 图 1-2 双缝干涉