
第五章光的偏振 本章讨论的主要问题是:(一)自然光经过各种偏振元件时,偏振状态如何变化。(二) 光经过偏振元件时,偏振光强度如何变化。 §5-1 自然光与偏振光 一、光的偏振性,线偏振光 横波的振动方向对传播方向不具有对称性,我们把这种不对称性叫做偏振。它是横波 区别于纵波的一个最明显标志,只有横波才有偏振现象。 光波是电磁波,光波中的电振动矢量E和磁振动矢量万都与传播速度五垂直,因此光 波是横波,它具有偏振性。E称为光矢最,E的振动称为光振动。光的横波性只表明电矢 量与光的传播方向垂直,在与传播方向垂直的平面内还可能有各种各样的振动状态。如果光 在传播过程中电矢量的振动只限于某一确定平面内,则这种光称为平面偏振光。由于平面偏 振光的电矢量在与传播方向垂直的平面上的投影为一条直线,故又称为线偏振光。 常用下图表示平面偏振光。电矢量和传播方向所构成的平面称为偏振光的振动面。 1111↓ (a) 图5-1 二、自然光 普通光源发出的光一般是自然光,自然光不能直接显示出偏振现象,这一点可以从光 源的微观发光机制来认识。每个发光原子每次所发射的是一个平面偏振波列。而各个原子的 发光是一个自发辐射的随机过程,彼此没有关联。各波列的偏振方向及位相分布都是无规则 的。因此在同一时刻观察大量发光原子或分子的大量波列,不仅相互间无位相关系,而且电 矢量可以分布在轴对称的一切可能的方位上。另一方面,由于原子的发光持续时间约为 10,因此在观察时间内,电矢量也是轴对称分布的。也就是在轴对称的各个方向上电矢量 的时间平均值是相等的,具有这种特点的光叫自然光。 图5-2
第五章 光的偏振 本章讨论的主要问题是:(一)自然光经过各种偏振元件时,偏振状态如何变化。(二) 光经过偏振元件时,偏振光强度如何变化。 §5—1 自然光与偏振光 一、光的偏振性,线偏振光 横波的振动方向对传播方向不具有对称性,我们把这种不对称性叫做偏振。它是横波 区别于纵波的一个最明显标志,只有横波才有偏振现象。 光波是电磁波,光波中的电振动矢量 E 和磁振动矢量 H 都与传播速度u 垂直,因此光 波是横波,它具有偏振性。 E 称为光矢量, E 的振动称为光振动。光的横波性只表明电矢 量与光的传播方向垂直,在与传播方向垂直的平面内还可能有各种各样的振动状态。如果光 在传播过程中电矢量的振动只限于某一确定平面内,则这种光称为平面偏振光。由于平面偏 振光的电矢量在与传播方向垂直的平面上的投影为一条直线,故又称为线偏振光。 常用下图表示平面偏振光。电矢量和传播方向所构成的平面称为偏振光的振动面。 图 5-1 二、自然光 普通光源发出的光一般是自然光,自然光不能直接显示出偏振现象,这一点可以从光 源的微观发光机制来认识。每个发光原子每次所发射的是一个平面偏振波列。而各个原子的 发光是一个自发辐射的随机过程,彼此没有关联。各波列的偏振方向及位相分布都是无规则 的。因此在同一时刻观察大量发光原子或分子的大量波列,不仅相互间无位相关系,而且电 矢量可以分布在轴对称的一切可能的方位上。另一方面,由于原子的发光持续时间约为 10-8 s,因此在观察时间内,电矢量也是轴对称分布的。也就是在轴对称的各个方向上电矢量 的时间平均值是相等的,具有这种特点的光叫自然光。 图 5-2

在数学上,我们可以用任意两个振幅相等的非相干的,正交的线偏振光来表示自然光。 非相干波就是相对位相差作迅速而规则变化的波。 H 图5-3 令两非相干偏振光的振幅为A,A,则应有 Ax=Ay 若自然的强度为1。,则: 1=A+A=1+1 1=分 §5一2平面偏振光与部分偏振光 一、平面偏振光的电矢量表达式 E=Acos(0-kc)=(Ar元。+An元)cos(om-kc) 二、二向色性、偏振片 二向色性指的是有些晶体对不同方向振动的电矢量,具有选择吸收的性质。 广泛使用的二向色性片是一种透明的聚乙烯醇片,通过加热和延伸,使得它在特点方 向具有排列得很好的长链分子,然后将该片用碘溶液浸染,碘依次沿聚乙烯醇分子的直线排 列起来,与碘相联系的导电电子就能顺者那些分子上下循环流动。分子好象是微观的导线。 含有这种平行地排列起来的长链分子的薄膜叫做偏振片。当一束自然光射到偏振片上时,吸 收平行链长方向的电场分量,而与它垂直的电场分量则几平不受影响,结果透射光为一平面 偏振光。我们把偏振片上能透过电矢量振动的方向称为它的透振方向。像偏振片这样用于产 生偏振光的器件称为起偏器
在数学上,我们可以用任意两个振幅相等的非相干的,正交的线偏振光来表示自然光。 非相干波就是相对位相差作迅速而规则变化的波。 图 5-3 令两非相干偏振光的振幅为 Ax , Ay ,则应有 Ax Ay 若自然的强度为 0 I ,则: 2 0 2 2 0 I I I I A A I I x y x y x y §5—2 平面偏振光与部分偏振光 一、平面偏振光的电矢量表达式 cos( ) ( ) cos( ) 0 0 0 0 0 E A t kz A x A y t kz x y 二、二向色性、偏振片 二向色性指的是有些晶体对不同方向振动的电矢量,具有选择吸收的性质。 广泛使用的二向色性片是一种透明的聚乙烯醇片,通过加热和延伸,使得它在特点方 向具有排列得很好的长链分子,然后将该片用碘溶液浸染,碘依次沿聚乙烯醇分子的直线排 列起来,与碘相联系的导电电子就能顺着那些分子上下循环流动。分子好象是微观的导线。 含有这种平行地排列起来的长链分子的薄膜叫做偏振片。当一束自然光射到偏振片上时,吸 收平行链长方向的电场分量,而与它垂直的电场分量则几乎不受影响,结果透射光为一平面 偏振光。我们把偏振片上能透过电矢量振动的方向称为它的透振方向。像偏振片这样用于产 生偏振光的器件称为起偏器
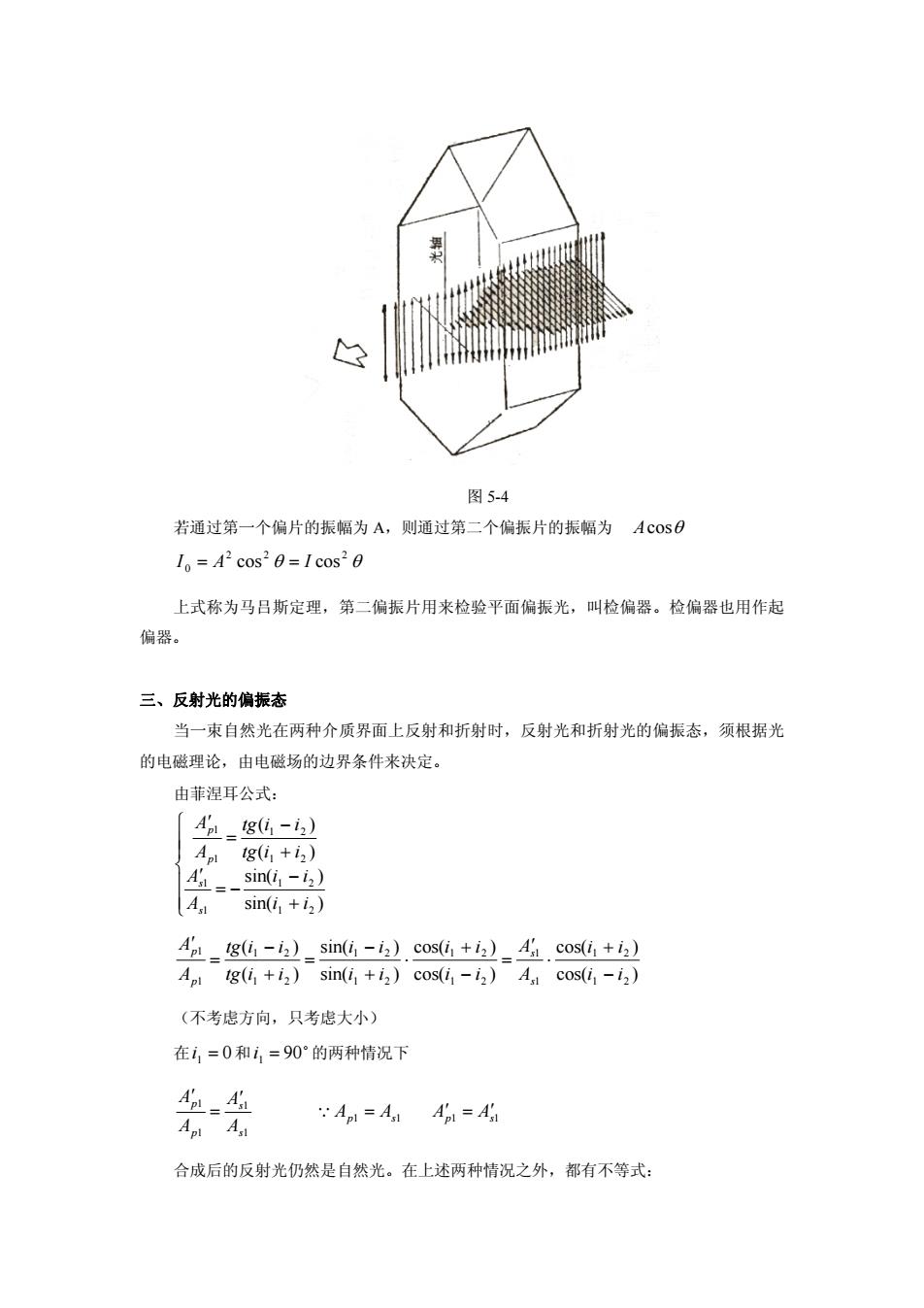
图5-4 若通过第一个偏片的振幅为A,则通过第二个偏振片的振幅为Acs( =42cos20=1cos20 上式称为马吕斯定理,第二偏振片用来检验平面偏振光,叫检偏器。检偏器也用作起 偏器。 三、反射光的偏振态 当一束自然光在两种介质界面上反射和折射时,反射光和折射光的偏振态,须根据光 的电磁理论,由电磁场的边界条件来决定。 由菲涅耳公式: 41=g-4】 Ag(6+2) =-sin-,) 4 sin(i+ (i -iz)_sin(i -iz)cos(in +iz)4 cos(in+iz) Ap tg(i +i)sin(i +i)cos(i -iz)A cos(i -i2) (不考虑方向,只考虑大小) 在,=0和1,=90°的两种情况下 Ap A An An 合成后的反射光仍然是自然光。在上述两种情况之外,都有不等式:
图 5-4 若通过第一个偏片的振幅为 A,则通过第二个偏振片的振幅为 Acos 2 2 2 0 I A cos I cos 上式称为马吕斯定理,第二偏振片用来检验平面偏振光,叫检偏器。检偏器也用作起 偏器。 三、反射光的偏振态 当一束自然光在两种介质界面上反射和折射时,反射光和折射光的偏振态,须根据光 的电磁理论,由电磁场的边界条件来决定。 由菲涅耳公式: sin( ) sin( ) ( ) ( ) 1 2 1 2 1 1 1 2 1 2 1 1 i i i i A A tg i i tg i i A A s s p p cos( ) cos( ) cos( ) cos( ) sin( ) sin( ) ( ) ( ) 1 2 1 2 1 1 1 2 1 2 1 2 1 2 1 2 1 2 1 1 i i i i A A i i i i i i i i tg i i tg i i A A s s p p (不考虑方向,只考虑大小) 在i1 0 和 i1 90 的两种情况下 1 1 1 1 1 1 1 1 p s p s s s p p A A A A A A A A 合成后的反射光仍然是自然光。在上述两种情况之外,都有不等式:
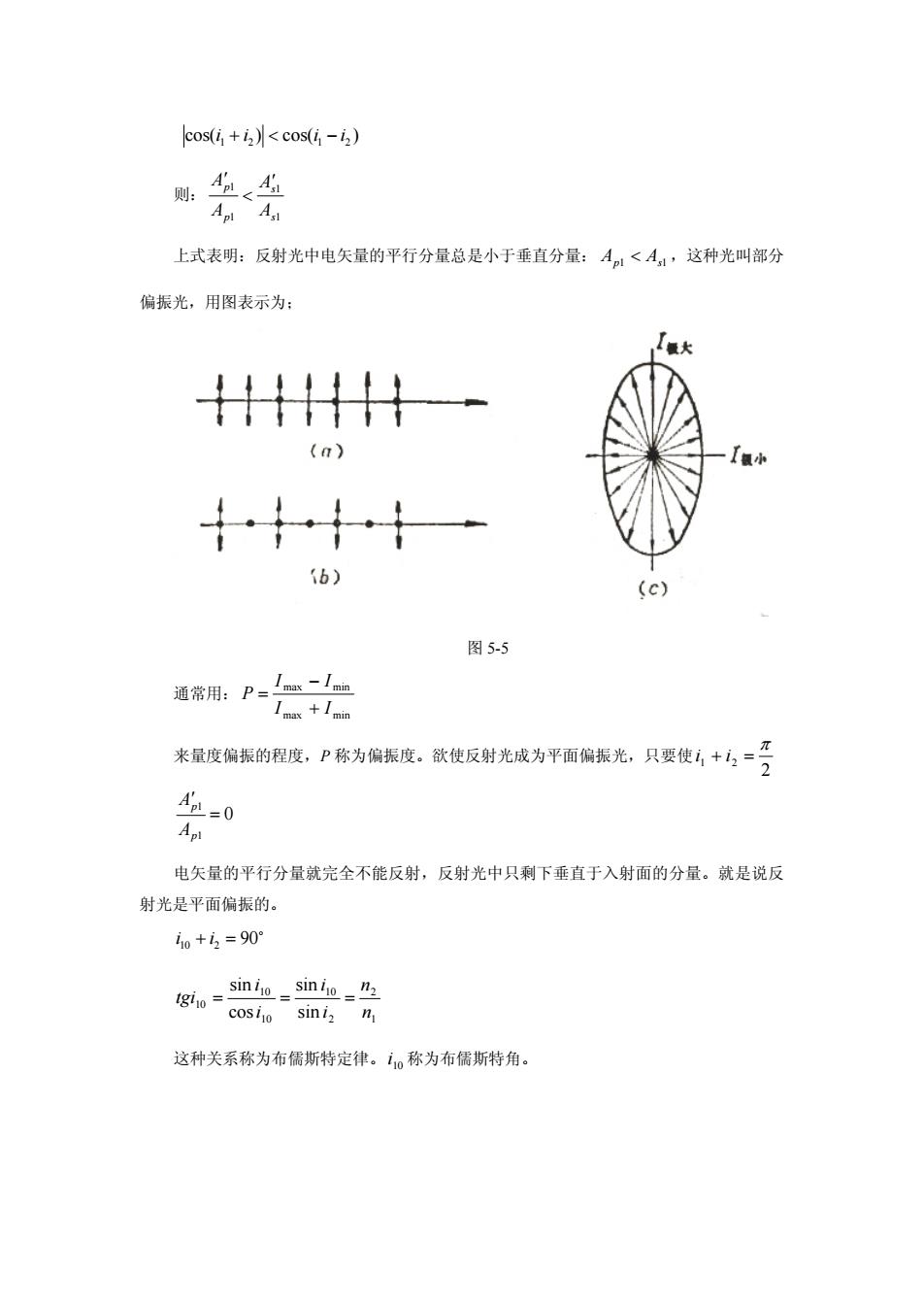
cos(+)<cos(i -iz 则玉丛 Ap A 上式表明:反射光中电矢量的平行分量总是小于垂直分量:A<A,这种光叫部分 偏振光,用图表示为: ti (a) i6) (c) 图5-5 来量度偏振的程度,P称为偏振度。欲使反射光成为平面偏振光,只要使:+一号 老0 电矢量的平行分量就完全不能反射,反射光中只剩下垂直于入射面的分量。就是说反 射光是平面偏振的。 10+5=90 这种关系称为布儒斯特定律。i。称为布儒斯特角
cos( ) cos( ) 1 2 1 2 i i i i 则: 1 1 1 1 s s p p A A A A 上式表明:反射光中电矢量的平行分量总是小于垂直分量: Ap1 As1 ,这种光叫部分 偏振光,用图表示为; 图 5-5 通常用: max min max min I I I I P 来量度偏振的程度,P 称为偏振度。欲使反射光成为平面偏振光,只要使 2 1 2 i i 0 1 1 p p A A 电矢量的平行分量就完全不能反射,反射光中只剩下垂直于入射面的分量。就是说反 射光是平面偏振的。 i 10 i2 90 1 2 2 10 10 10 10 sin sin cos sin n n i i i i tgi 这种关系称为布儒斯特定律。 10 i 称为布儒斯特角
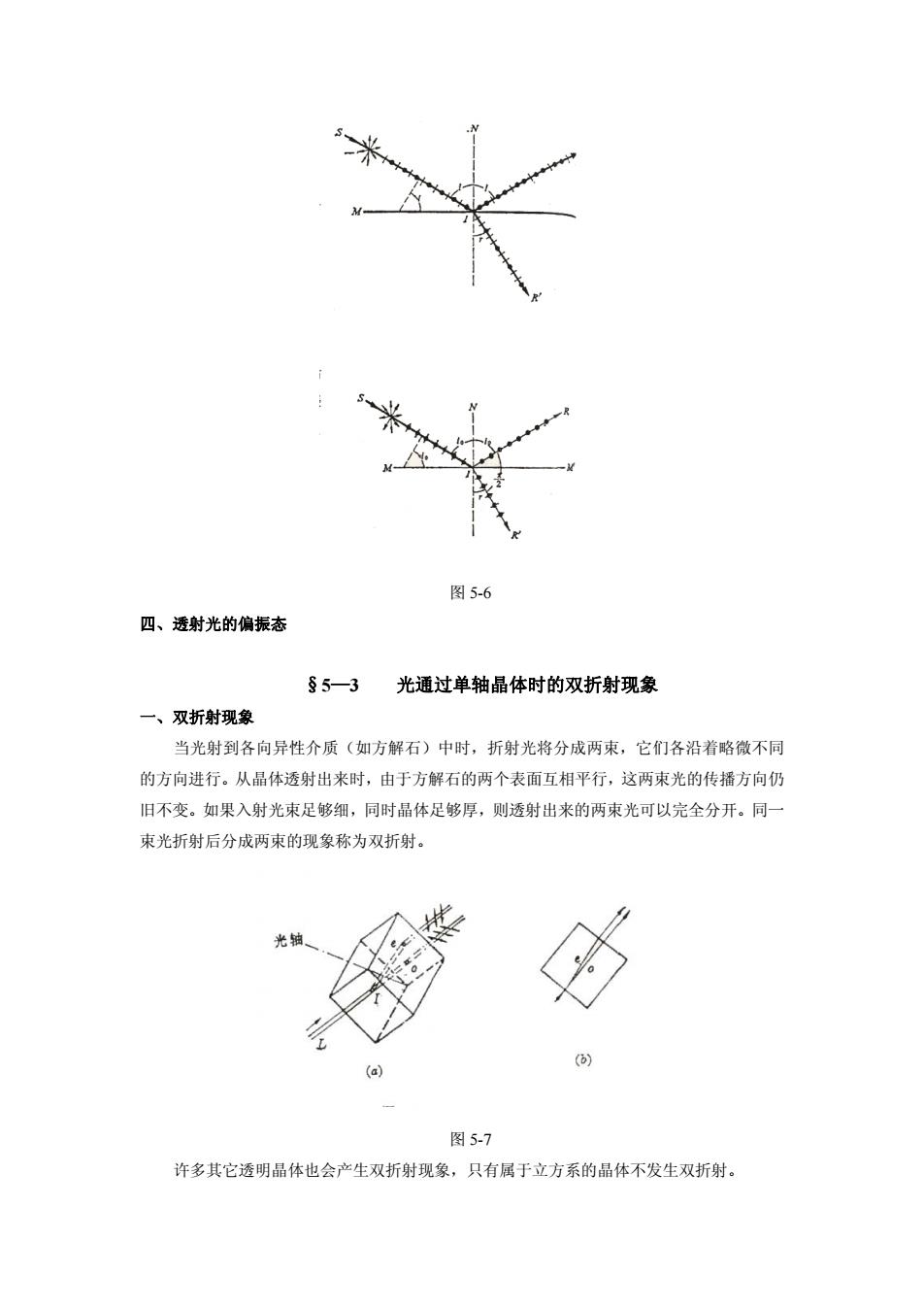
四、透射光的偏振态 §5-3 光通过单轴晶体时的双折射现象 一、双折射现象 当光射到各向异性介质(如方解石)中时,折射光将分成两束,它们各沿着略微不同 的方向进行。从晶体透射出来时,由于方解石的两个表面互相平行,这两束光的传播方向仍 旧不变。如果入射光束足够细,同时晶体足够厚,则透射出来的两束光可以完全分开。同一 束光折射后分成两束的现象称为双折射。 图5-7 许多其它透明晶体也会产生双折射现象,只有属于立方系的晶体不发生双折射
图 5-6 四、透射光的偏振态 §5—3 光通过单轴晶体时的双折射现象 一、双折射现象 当光射到各向异性介质(如方解石)中时,折射光将分成两束,它们各沿着略微不同 的方向进行。从晶体透射出来时,由于方解石的两个表面互相平行,这两束光的传播方向仍 旧不变。如果入射光束足够细,同时晶体足够厚,则透射出来的两束光可以完全分开。同一 束光折射后分成两束的现象称为双折射。 图 5-7 许多其它透明晶体也会产生双折射现象,只有属于立方系的晶体不发生双折射