
第一章光的干涉 §1一1光的电磁理论 ·十九世纪七十年代,麦克斯韦发展了电磁理论,从而导致电磁波的发 现。电磁波在不同介质的界面上发生反射和折射现象,在传播中出现 干涉、衍射和偏振现象,而根据当时已有的知识,光波也具有完全相 似的干涉、衍射和偏振等现象,它们之间有什么联系呢?电磁波在真 空中的速度 C三 在实验误差范围以内,这个常数c与已测得的光速相等。于是麦克 斯韦得出这样的理论:光是某二波段的电磁波,©就是光在真空中的 传播速度
第一章 光的干涉 §1—1 光的电磁理论 ⚫ 十九世纪七十年代,麦克斯韦发展了电磁理论,从而导致电磁波的发 现。电磁波在不同介质的界面上发生反射和折射现象,在传播中出现 干涉、衍射和偏振现象,而根据当时已有的知识,光波也具有完全相 似的干涉、衍射和偏振等现象,它们之间有什么联系呢?电磁波在真 空中的速度 在实验误差范围以内,这个常数c与已测得的光速相等。于是麦克 斯韦得出这样的理论:光是某一波段的电磁波,c就是光在真空中的 传播速度
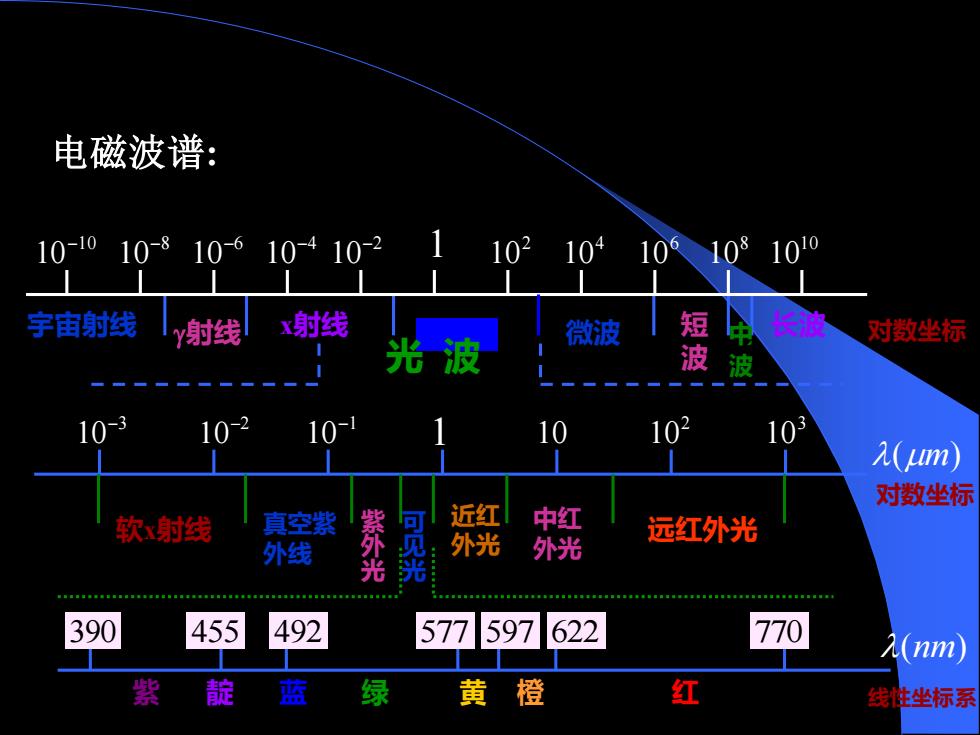
电磁波谱: 10-1010-810-610410-2 102104106108 1010 宇宙射线 y射线 射线 微波 短 光波 对数坐标 波波 10-3 10-2 10- 10 102 103 2(um) 对数坐标 软x射线 真空紫 近红 中红 远红外光 外线 紫外光 外光 外光 390 455 492 577597622 770 A(nm) 紫 靛 蓝 绿 黄橙 红 线性坐标系
电磁波谱: 宇宙射线 射线 x射线 光波 微波 短 波 中` 波 长波 10 10− 8 10− 6 10− 4 10− 2 10− 2 10 4 10 6 10 8 10 10 10 (m) 1 对数坐标 2 10 3 − 10− 10 2 10 3 1 10 1 10− (m) 对数坐标 软x射线 真空紫 外线 紫 外 光 可 见 光 近红 外光 中红 外光 远红外光 390 455 492 577 597 622 770 (nm) 紫 靛 蓝 绿 黄 橙 红 线性坐标系 光 波

介质中电磁波的速度为 折射率 n= 光学材料是非铁磁质,1 真空中传播的电磁波方程为 02E o-B V2E=8o40 V2B=8040 上两式的简谐解是 E=E cos(@t-kr+). B=B。cos(ot-kr+p)
介质中电磁波的速度为 折射率 光学材料是非铁磁质, =1, r . n r = 真空中传播的电磁波方程为 , 2 2 0 0 2 t = E E . 2 2 0 0 2 t = B B 上两式的简谐解是 cos( ), +0 E = E − k r 0 t cos( ). 0 +0 B = B t − k r

和都垂直元,电磁波是横波。维纳实验证 明,对人的眼晴或感光仪器起作用的是电场强 度,所以光波中的振动矢量是指电场强度E。 电磁波中能为人眼所感受的波长在3900A~7600A 之间,对应的频率范围7.5×1014~4.1×1014Hz。 。人眼的视网膜或物理仪器所检测到的光的强弱都 是由能流密度的大小来决定的(单位时间内通过 与波的传播方向垂直的单位面积的能量)。 任何波动所传递的能流密度与振幅的平方成正比, 所以,光的强度或光照度(即接受到的平均能流 密度)为 Io A? (A为电场强度) 在波动光学中,主要是讨论光波所到之处的相对光 照度。因而通常只需计算光波在各处的振幅的平 方值,而不需要计算各处的光照度的绝对值
和 都垂直 ,电磁波是横波。维纳实验证 明,对人的眼睛或感光仪器起作用的是电场强 度 ,所以光波中的振动矢量是指电场强度 。 ⚫ 电磁波中能为人眼所感受的波长在3900Å~7600Å 之间,对应的频率范围7.5×1014~4.1×1014Hz。 ⚫ 人眼的视网膜或物理仪器所检测到的光的强弱都 是由能流密度的大小来决定的(单位时间内通过 与波的传播方向垂直的单位面积的能量)。 ⚫ 任何波动所传递的能流密度与振幅的平方成正比, 所以,光的强度或光照度(即接受到的平均能流 密度)为 (A为电场强度) 在波动光学中,主要是讨论光波所到之处的相对光 照度。因而通常只需计算光波在各处的振幅的平 方值,而不需要计算各处的光照度的绝对值。 2 I A

§1—2波动的独立性、叠加性 简谐波的表达式 一、机械波的独立性和叠加性 在机械振动和机械波中我们已注意到从几个振源发出的波相遇于同一 区域时,只要振动不十分强烈,就可以保持自己的特性(频率、振幅 和振动方向等),按照自己原来的传播方向继续前进,彼此不受影响。 这就是波动独立性的表现。 ·在相遇区域内,介质中一点的合位移是各波单独传播时在该点所引起 的位移的矢量和,因此,可以简单的,没有任何畸变地把各波的分位 移按照矢量加法叠加起来,这就是波动的叠加性。这种叠加性是以独 立性为条件的,是最简单的叠加。 通常情况下,波动方程是线性微分方程,简谐波的表达式就是它的 个解。如果有两个独立的函数都能满足同一个给定的微分方程,那么 这两个函数的和也必然是这个微分方程的解。这就是两个具有独立性 的波的叠加的数学意义
§1—2 波动的独立性、叠加性 简谐波的表达式 一、机械波的独立性和叠加性 ⚫ 在机械振动和机械波中我们已注意到从几个振源发出的波相遇于同一 区域时,只要振动不十分强烈,就可以保持自己的特性(频率、振幅 和振动方向等),按照自己原来的传播方向继续前进,彼此不受影响。 这就是波动独立性的表现。 ⚫ 在相遇区域内,介质中一点的合位移是各波单独传播时在该点所引起 的位移的矢量和,因此,可以简单的,没有任何畸变地把各波的分位 移按照矢量加法叠加起来,这就是波动的叠加性。这种叠加性是以独 立性为条件的,是最简单的叠加。 ⚫ 通常情况下,波动方程是线性微分方程,简谐波的表达式就是它的一 个解。如果有两个独立的函数都能满足同一个给定的微分方程,那么 这两个函数的和也必然是这个微分方程的解。这就是两个具有独立性 的波的叠加的数学意义