《光学》课程授课教案（讲义）几何光学的基本原理

光学第三章儿何光学的基本原理 第三章几何光学 §3.1基本概念及定律 1、光线与波面 2、基本定律（实验规律） (1)光在均匀介质中沿直线传播 例：不均匀介质中，光线弯曲（太阳落山） (2)光的反射和折射定律 A、反、折线同在入射面内，并与入射线分居两侧 B、ir=i S_生=1（第二媒质相对第一媒质的相对折射率） C.siniz 例：如反射面凹凸不平，且线度远大于波长，形成浸反射。 (3)光的独立性，光路可逆原理 3、统一性（折、反、直） nsin4=nsin2,专=4（值传） 乃=-n, 4=-1反射（坐标反演） n≠n2 折射 §3.2费马原理 概括了光线传播所遵循的规律 光沿光程值为极小、极大或恒定（极值）的路径传播。 食ndk=极值 6∫nd=0 大多数情况下是极小： 例：用费马原理导出折射定律（光程极小） 光：A→B nn 过A、B两点作垂直于界面的平面，交线 00 L上（即入射面内）

光学 第三章 几何光学的基本原理 第三章 几何光学 §3.1 基本概念及定律 1、光线与波面 2、基本定律（实验规律） （1）光在均匀介质中沿直线传播 例：不均匀介质中，光线弯曲（太阳落山） （2）光的反射和折射定律 A、反、折线同在入射面内，并与入射线分居两侧 B、 11  ii  C、 21 1 2 2 1 sin sin n n n i i  （第二媒质相对第一媒质的相对折射率） 例：如反射面凹凸不平，且线度远大于波长，形成漫反射。 （3）光的独立性，光路可逆原理 1) sin sin (, sin sin 2 1 1221 2 1  i i nn i i 3、统一性（折、反、直） 折射 反 坐标反演 直传 , 射（ ） sin ,sin )( 21 12 12 2211 12 nn nn li iiinin       §3.2 费马原理 概括了光线传播所遵循的规律 光沿光程值为极小、极大或恒定（极值）的路径传播。   A B nds 极值    B A nds 0 大多数情况下是极小： 例：用费马原理导出折射定律（光程极小） 1 光：  BA 21 nn 过 A、B 两点作垂直于界面的平面，交线 OO  证明：（1）据费马原理，折射点必在 OO  上（即入射面内）

光学第三章几何光学的基本原理 反证，如在C',作垂线CC⊥O0上（即入射面内） AC>AC CB>C"B (AC'B)>(AC"B) C使光程不为极小 因而，折射点C必在00上，入、折两面在同一平面内 (2)确定C点的位置（在OO'上） A(x).B(x2.y2).C(x,o) 必有x<x<x2 (ACB)=nAC+nCB =mVx-x)2++m2V32-x2+月 d(A+B)_ m(x-x)n(x2-x)+y dx x-x)+片Vx2-x)2+月 -C_n,CB AC CB =m sini -n siniz =0 同理可导出反射定律 费马原理不涉及光沿哪个方向传播，只涉及路径，光从A→B,与B→A,光程为极值的 条件相同。因此，两种情况下，光沿同一路径传播，即费马原理中本身包含了光的可逆性。 许多情况下，也有光沿极大，恒定的路径传播。 例2旋转椭球面 光过焦点，在镜面反射，必过另一焦点。 即(D4,+A卫)=常数(1) (bi (b)光程取极小 (c)光程取极大

光学 第三章 几何光学的基本原理 反证，如在C，作垂线   OOCC 上（即入射面内） )()( C 使光程不为极小          BCABCA BCBCCACA 因而，折射点 C 必在 上，入、折两面在同一平面内 OO  （2）确定 C 点的位置（在 OO  上） ),( ),( ),( 11 22 oxCyxByxA 必有 1 2  xxx )( 1  2CBnACnACB 2 2 2 22 2 1 2 1 1 )( )(  yxxnyxxn sin 0sin )( )( )( )( )( 2211 1 2 2 2 2 2 2 2 2 22 2 1 2 1 1 1             inin CB BCn AC CAn yxx yxxn yxx xxn dx BAd 同理可导出反射定律 费马原理不涉及光沿哪个方向传播，只涉及路径，光从 ，与 ，光程为极值的 条件相同。因此，两种情况下，光沿同一路径传播，即费马原理中本身包含了光的可逆性。  BA  AB 许多情况下，也有光沿极大，恒定的路径传播。 例 2 旋转椭球面 光过焦点，在镜面反射，必过另一焦点。 即 ( ) 1  ii PAAP 2 =常数 （1） （b）光程取极小 （c）光程取极大 2

光学第三章儿何光学的基本原理 例3物象关系的等光程性 光线1,2,3应取极值，如均为极大，极小或恒定则(PP)仍是一恒定值 S3.3成象的基本概念 一、单心光束和象散光束 (1)单心光束：一光束中各光线或其延长线相交于一点 (2)象散光束：单心光束经折、反后，不再相交于一点，各光线也不平行，这称为象散光束。 二、物和象物空间象空间 实物：入射的发散光束的心。 通常的实物各方向均可看到 但光学上的实物还可是前一光学元件成的实象 虚物：入射到系统上的单心束是会聚的，且尚未会聚于单心就与光学系统相遇，光线的延长 线的交点便是虚物。 实象：可继续发散，在屏上有亮点，有漫反射，出射光束的光点。 虚象：出射光束反向延长线的交点，不能在屏上呈现，可用眼睛观察。 入射光线所在的空间实物在物空间，虚物不在 象空间：出射光线所在的空间实象在象空间，虚象不在。 反射时，物空间与象空间重迭 三、理想光学系统，物象之间的共轭性 任何单心光束通过系统后仍保持为单心（理想） (1)物空间每个点对应象空间一点 (2)物空间每个直线对应象空间直线 (3)物空间每个平面对应象空间平面 相应的点、线、面称为共轭点、线、面它们具共轭性。 除平面镜外，任何实际的光学系统都不可能达到理想成象的要求，共轭系统在近轴条件下可近

光学 第三章 几何光学的基本原理 例 3 物象关系的等光程性 1 2 3 光线 1，2，3 应取极值，如均为极大，极小或恒定则（ PP ）仍是一恒定值。 §3.3 成象的基本概念 一、单心光束和象散光束 （1）单心光束：一光束中各光线或其延长线相交于一点 （2）象散光束：单心光束经折、反后，不再相交于一点，各光线也不平行，这称为象散光束。 二、物和象 物空间 象空间 实物：入射的发散光束的心。 通常的实物各方向均可看到 但光学上的实物还可是前一光学元件成的实象 虚物：入射到系统上的单心束是会聚的，且尚未会聚于单心就与光学系统相遇，光线的延长 线的交点便是虚物。 实象：可继续发散，在屏上有亮点，有漫反射，出射光束的光点。 虚象：出射光束反向延长线的交点，不能在屏上呈现，可用眼睛观察。 入射光线所在的空间实物在物空间，虚物不在 象空间：出射光线所在的空间实象在象空间，虚象不在。 反射时，物空间与象空间重迭 三、理想光学系统， 物象之间的共轭性 任何单心光束通过系统后仍保持为单心（理想） （1）物空间每个点对应象空间一点 （2）物空间每个直线对应象空间直线 （3）物空间每个平面对应象空间平面 相应的点、线、面称为共轭点、线、面它们具共轭性。 除平面镜外，任何实际的光学系统都不可能达到理想成象的要求，共轭系统在近轴条件下可近 3

光学第三章儿何光学的基本原理 似看作理想光学系统。 即近轴光线、近轴物的条件 §3.4光在平面界面上的反射和折射 一、光在平面上的反射 平面镜是最简单，不改变单心性的光学系统。 PN=P'N P对P是对称的，不改变光束的单心性。 二、单心性的破坏（光在平面上的折射） > B A(x1,0),A2(32,0) p(o,y),p(oyP2(o,乃2) p:￥=5-g7 .)为 哈-径 折射后，所有光线不交于一点，而是交于两条互相垂直的线段上。（将图绕y轴转过一个小角 度) PP:弧矢象线 由p'点所描出的垂直于图面的象线叫子午象线。 说明：当4=0时 r=0=为=为受 y':象似深度 大象的清晰度由于象散而破坏。 4

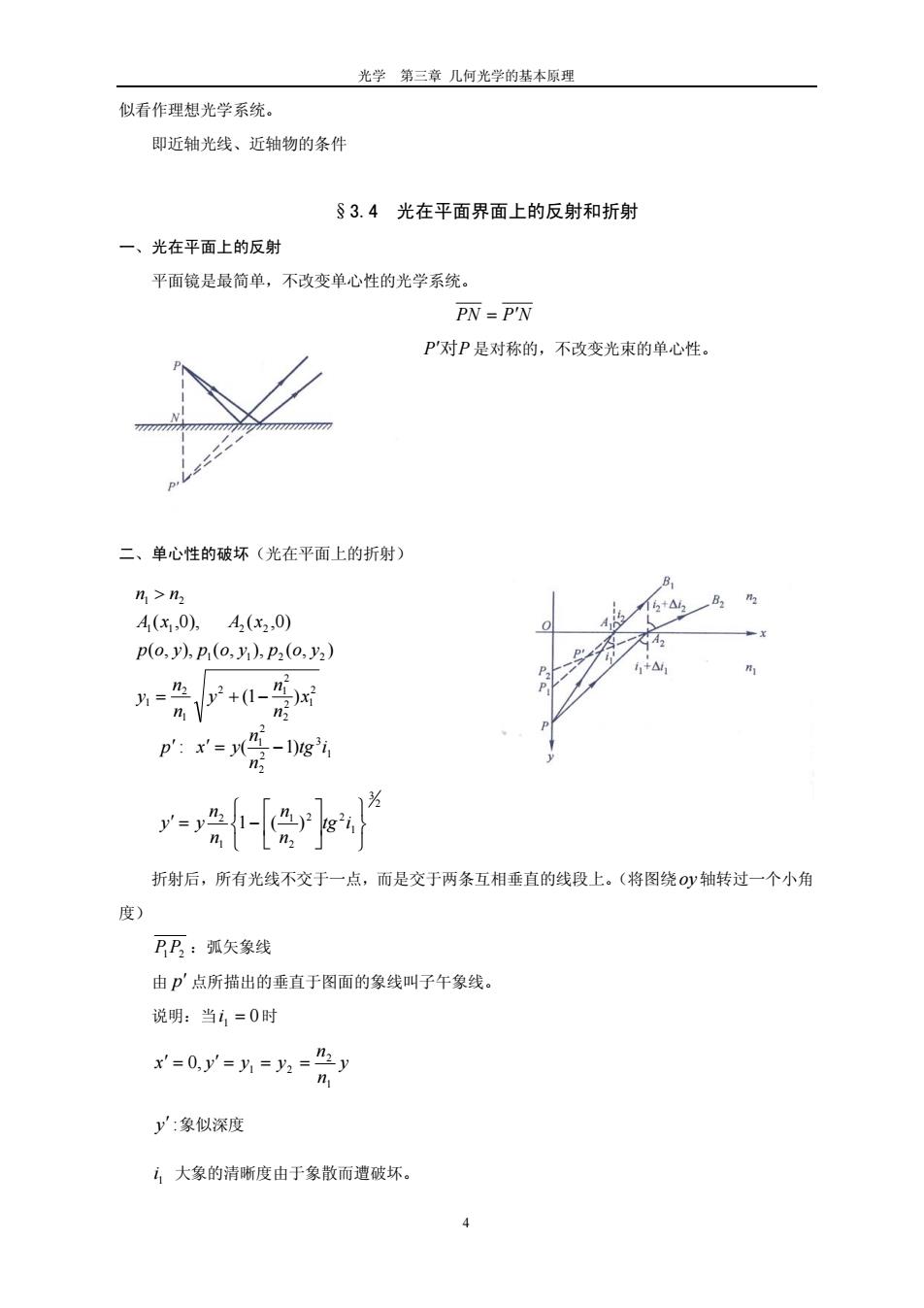
光学 第三章 几何光学的基本原理 似看作理想光学系统。 即近轴光线、近轴物的条件 §3.4 光在平面界面上的反射和折射 一、光在平面上的反射 平面镜是最简单，不改变单心性的光学系统。  NPPN 对PP 是对称的，不改变光束的单心性。 二、单心性的破坏（光在平面上的折射） 1 3 2 2 2 1 )1( : itg n n  yxp  2 2 1 2 2 2 1 1 2 1 2211 11 22 21 )1( ),(),(),( )0,( ),0,( x n n y n n y yopyopyop xAxA nn   2 3 1 22 2 1 1 2 )(1               itg n n n n yy 折射后，所有光线不交于一点，而是交于两条互相垂直的线段上。（将图绕 轴转过一个小角 度） oy PP 21 ：弧矢象线 由 点所描出的垂直于图面的象线叫子午象线。 p 说明：当 时 0 i 1  y n n yyyx 1 2 21   ,0   y :象似深度 1 i 大象的清晰度由于象散而遭破坏。 4

光学第三章儿何光学的基本原理 例1使一束向p点会聚的光到P点之前通过一平行玻璃板，如果将玻璃板垂直于光束的轴 竖放，向会聚点将朝哪个方向移动？移动多少距离？ 解：方法一 会聚光通过板发生两次折射，折射后光束向外侧移p→p',即求p叩。 通过1面折射sn4 =n 面甜 六5=2，=4 APICP 出射光线对入射线侧移 -配4-6热-6) m- =hm40-2 cost=-sin1-(sin, .d=hsini (1- coSl 你-sim7 则p币=g,=d-cos4-匠-5m cosi. )与1有关，单心光束，1不同，象散 令1=0。 m=-动 方注直接用了=产 经1面：川=山===心 经2面：为2=-h,n=nn=1 y=EP-以-M

光学 第三章 几何光学的基本原理 例 1 使一束向 p 点会聚的光到 p 点之前通过一平行玻璃板，如果将玻璃板垂直于光束的轴 竖放，向会聚点将朝哪个方向移动？移动多少距离？ 解：方法一 会聚光通过板发生两次折射，折射后光束向外侧移  pp ，即求 pp  。 通过 1 面折射 n i i  2 1 sin sin 2 面 折射 ni i 1 sin sin 1 2    1122    ,   iiii // PCAP  出射光线对入射线侧移 )sin( cos )sin( 21 2 21 ii i h iiBCd   )sincoscos(sin cos 21 21 2 iiii i h   2 2 1 2 2 1 2 2 1 1 )sin 1 (1sin1cos ) sin sin cos cos 1(sin i n i i i i i i ih   ) sin cos 1(sin 1 2 2 1 1 in i ihd    则 ) sin cos 1(cos 1 2 2 1 1 1 in i id tgi PP d   与 有关，单心光束， 不同，象散 1 i 1 i 令i 1  0 。 ) 1 1( n  hpp  y n n y 1 2 方法二，直接用   经 1 面： 1 2  . 1   nyynnn 2 3 ,1 经 2 面： 1 , ,  12  1 nnnhyy 2  )( 1 1 hy n   PEy     5