
第七章光的量子性 良见本意本要价中支在究毯一光电效位和指领效应时。怎样打破经典理的 二象性,并阐述波粒二象性的含义。 §7一1热辐射、基尔霍夫定律 一、几种不同形式的辐射 物体向外辐射将消耗本射的能量。要长期维持这种辐射,就必须不断从外面补偿能量, 否则辐射就会引起物质内部的变化。在辐射过程中物质内部发生化学变化的,叫做化学发 光。用外来的光或任何其它铝射不斯地或预先地照射物质而使之发光的过程叫做光致发光 由场的作用引起的辐射叫场致发光。另 种辐射叫做热辐射,这种辐射在量值方面和按波 长分布方面都取决全辐射体的温度。 任何温度的物体都发出一定的热辐射。 一物体500℃左右,暗红色。随温度不断上升,辉光逐渐亮起来,而且波长较短的 辐射越来越多。1500℃变成明亮的白炽光。同一物体在一定温度下所辐射的能量,在不同 光谱区域的分布是不均匀的,而且温度越高。 光谱中与 能量最大的辐射相对应的频率也越 高。在一定温度下,不同物体所辐射的光谱成份有显著的不同。 、辐射出射度和吸收比 从上面知道:在单位时间内从物体单位面积向各个方向所发射的,须率在y→V+dy 范围内的辐射能量d炒与y和T有关,而且dv足够小时,可认为与dy成正比 dΦ.r=Edy E,是V和T的函数,叫做该物体在温度T时发射频率为V的单色辐射出射度(单色 辐出度)。它的物理意义是从物体表面单位面积发出的,频率在v附近的单位频率间隔内的 辐射功率。它反映了在不同温度下,辐射能量按频率分布的情况。单位为 从特体表面单位面积上所发出的各种频率的总辐射功率,称为物体的辐射出射度。用 Φ(T)表示: Φ(T)=广dmr=Erd 中(T)只是温度的函数。E,和中(T)同表面情况有关。 另一方面,当辐射照射到某一不透明物体表面时,其中一部分能量将被物体散射或反 射,另一部分能量则被物体所吸收。用心,表示频率在v和v+dv范围内照射到温度为 T的物体的单位面积上的辐射能量: ,表示物体单位面积上所吸收的辐射能量,则 dΦ 叫做该物体的吸收比
第七章 光的量子性 本章主要介绍历史上在研究黑体辐射,光电效应和康普顿效应时,怎样打破经典理论 成见,逐渐认识到光的波粒二象性,并阐述波粒二象性的含义。 §7—1 热辐射、基尔霍夫定律 一、几种不同形式的辐射 物体向外辐射将消耗本射的能量。要长期维持这种辐射,就必须不断从外面补偿能量, 否则辐射就会引起物质内部的变化。在辐射过程中物质内部发生化学变化的,叫做化学发 光。用外来的光或任何其它辐射不断地或预先地照射物质而使之发光的过程叫做光致发光。 由场的作用引起的辐射叫场致发光。另一种辐射叫做热辐射,这种辐射在量值方面和按波 长分布方面都取决全辐射体的温度。 任何温度的物体都发出一定的热辐射。 一物体 500℃左右,暗红色。随温度不断上升,辉光逐渐亮起来,而且波长较短的 辐射越来越多。1500℃变成明亮的白炽光。同一物体在一定温度下所辐射的能量,在不同 光谱区域的分布是不均匀的,而且温度越高,光谱中与能量最大的辐射相对应的频率也越 高。在一定温度下,不同物体所辐射的光谱成份有显著的不同。 二、辐射出射度和吸收比 从上面知道:在单位时间内从物体单位面积向各个方向所发射的,频率在 d 范围内的辐射能量 d 与 和 T 有关,而且 d 足够小时,可认为与 d 成正比 d ,T ET d E ,T 是 和 T 的函数,叫做该物体在温度 T 时发射频率为 的单色辐射出射度(单色 辐出度)。它的物理意义是从物体表面单位面积发出的,频率在 附近的单位频率间隔内的 辐射功率。它反映了在不同温度下,辐射能量按频率分布的情况。单位为 W m J m s 2 2 / / 从特体表面单位面积上所发出的各种频率的总辐射功率,称为物体的辐射出射度。用 ( ) 0 T 表示: T d T E ,T d 0 , 0 0 ( ) ( ) 0 T 只是温度的函数。 E ,T 和 ( ) 0 T 同表面情况有关。 另一方面,当辐射照射到某一不透明物体表面时,其中一部分能量将被物体散射或反 射,另一部分能量则被物体所吸收。用 d ,T 表示频率在 和 d 范围内照射到温度为 T 的物体的单位面积上的辐射能量; d ,T 表示物体单位面积上所吸收的辐射能量,则 T T T d d A , , , 叫做该物体的吸收比

0≤A,≤1,吸收比同y,T,和物体及表面情况有关。 三、基尔霍夫定律 Ex和A,之间有若一定的联系。 将温度不同的物体P,P,P,放在一个密闭的理想绝热容器里,如果容器内部是真空 的,则物体与容器之间及物体与物体之间只能通过辐射和吸收来交换能量,当单位时间内 辐射体发出的能量比吸收的较多时,它的温度就下降,这时辐射就会减弱, ,相反辐射将封 强。经过一段时间,系统将建立热平衡,此时各物体在单位时间内发出的能量恰好等于吸 收的能量。由此可见,在热平衡的情况下。由此可见,在热平衡的情况下,单色辐出度较 大的物体,其吸收比也一定较大。1859年,基尔霍夫指出:物体的=化刀与物休 的性质无关,而只是频率和温度的普适函数。 图7-1 §7一2黑体辐射 一、黑体 冬种物体由手它们有不同的结构.因面它对外来辐射的吸收,以及它本射对外的辐 都不相同 但是有 类物体其表面 不反射光, 它们能够在任何温度下吸收射来的一切电磁 辐射,这类物体就叫做约对黑体。处于热平衡时,黑体具有最大的吸收比,因而它也就有
0 A ,T 1,吸收比同 ,T ,和物体及表面情况有关。 三、基尔霍夫定律 E ,T 和 A ,T 之间有着一定的联系。 将温度不同的物体 P1,P2,P3 放在一个密闭的理想绝热容器里,如果容器内部是真空 的,则物体与容器之间及物体与物体之间只能通过辐射和吸收来交换能量,当单位时间内 辐射体发出的能量比吸收的较多时,它的温度就下降,这时辐射就会减弱。相反辐射将增 强。经过一段时间,系统将建立热平衡,此时各物体在单位时间内发出的能量恰好等于吸 收的能量。由此可见,在热平衡的情况下。由此可见,在热平衡的情况下,单色辐出度较 大的物体,其吸收比也一定较大。1859 年,基尔霍夫指出:物体的 ( , ) , , f T A E T T 与物体 的性质无关,而只是频率和温度的普适函数。 图 7-1 §7—2 黑体辐射 一、黑体 各种物体由于它们有不同的结构,因而它对外来辐射的吸收,以及它本射对外的辐射 都不相同。但是有一类物体其表面不反射光,它们能够在任何温度下吸收射来的一切电磁 辐射,这类物体就叫做约对黑体。处于热平衡时,黑体具有最大的吸收比,因而它也就有
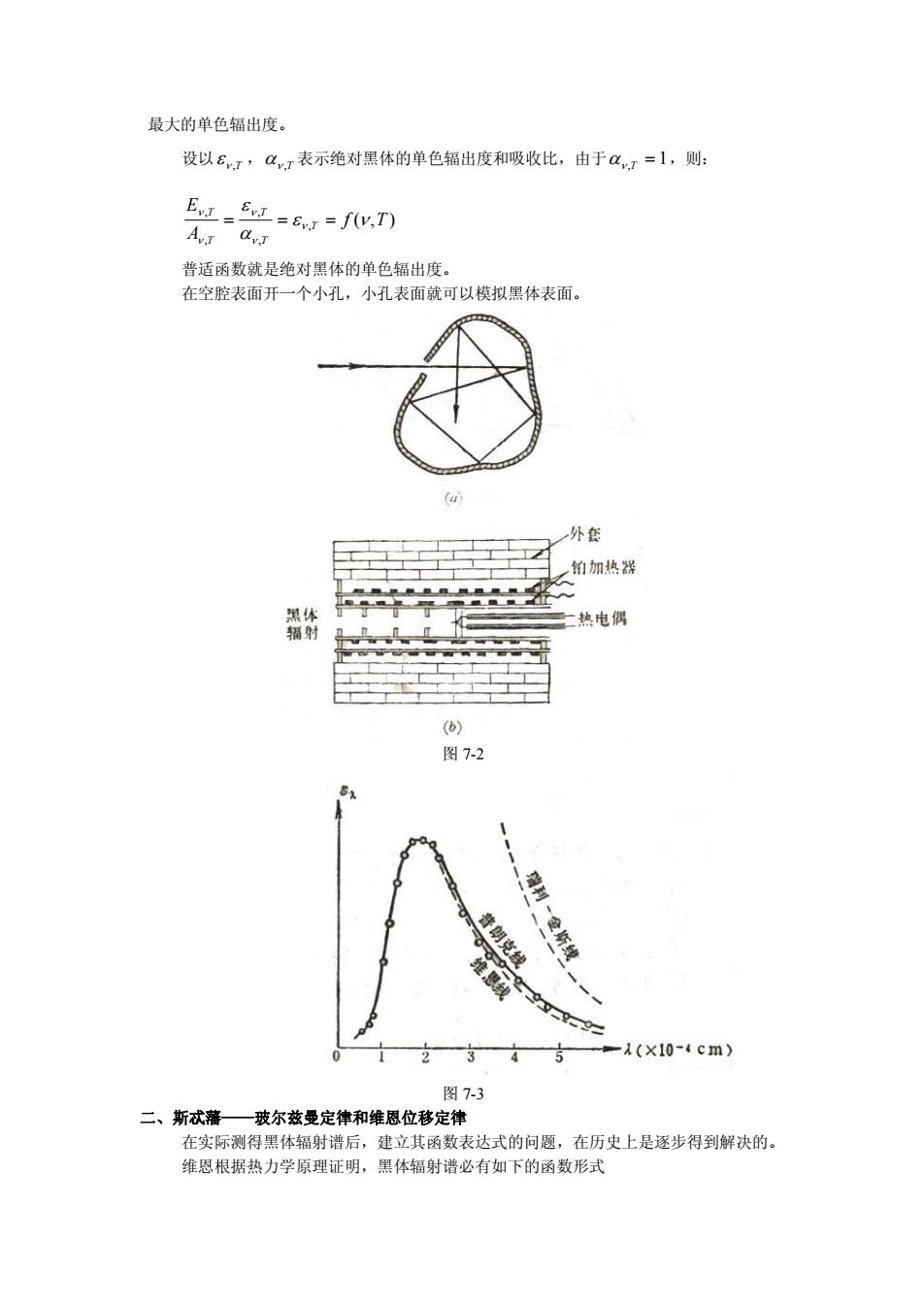
最大的单色辐出度。 设以6,ar表示绝对黑体的单色辐出度和吸收比,由于a=1,则: EL-1=6a=fw刀 Avt dvt 普适函数就是绝对黑体的单色辐出度。 在空腔表面开一个小孔,小孔表面就可以模拟黑体表面。 外套 铂加热器 热电偶 图7-2 01235 -(x10-4cm 图7-3 二、斯忒藩 —一玻尔兹曼定律和维恩位移定律 在实际测得黑体辐射谱后,建立其函数表达式的问题,在历史上是逐步得到解决的。 维恩根据热力学原理证明,黑体辐射谱必有如下的函数形式
最大的单色辐出度。 设以 ,T , ,T 表示绝对黑体的单色辐出度和吸收比,由于 ,T 1,则: ( , ) , , , , , f T A E T T T T T 普适函数就是绝对黑体的单色辐出度。 在空腔表面开一个小孔,小孔表面就可以模拟黑体表面。 图 7-2 图 7-3 二、斯忒藩——玻尔兹曼定律和维恩位移定律 在实际测得黑体辐射谱后,建立其函数表达式的问题,在历史上是逐步得到解决的。 维恩根据热力学原理证明,黑体辐射谱必有如下的函数形式

6w=份}戌w-号分)v=号=京 其中∫',f的函数形式尚不能完全确定,利用上式可得下列两条定律(1893年) (1)黑体的辐出度与绝对温度T的四次方成正比。即: Φ(T)=广6rdv=ot g=5.67×10-W1m2.k是一个普适常数 (1879年斯忒藩从实验观察到,1884年玻尔兹曼从理论上给出上式称为斯忒藩一玻 尔兹曼定律。) (2)任何温度下,627都有一极大值,令这极大值对应的波长为元,则 Aut =b b=2.89×10-3mk 这个规律称为维恩位移定律。 三、维思公式和瑞利金斯公式 单纯从热力学原理出发,而不对辐射机制作任何具体的假设是不能将∫'和∫的函数形 式进一步具体化的,历史上在这个问题获得最终的正确答案之前,有过下列两个公式,它 们对揭露经典物理的矛盾起了重大的作用。 (1)1896年,维恩假设气体分子辐射的频率v只是与其速度D有关(这一假设看来 是没有什么根据的),从而得到与麦克斯韦速度分布律形式很相似的公式。 e-Duir % a,B为常数,上式称为维恩公式。 (2)瑞利一金斯定律 1900年瑞利与金斯试图把能量均分定律应用到电磁辐射能量度按率额的情况中。 他们假设空腔处于热平衡时的辐射场将是一些驻波,根据能量均分定理,每一列驻波斯湾 平均能量E=kT,与频率无关,这样可以算出 6=2或 2 上式称为瑞利一金斯公式。 两公式都符合普遍形式。 同实验数据比较,在短波区域维恩公式符合的很好,但在长波范围则有虽不太大但却 是系统的偏离。瑞利公式与之相反,在长波部分符合的很好,但在短波波段偏离非常大, 不仅如此:1→0,62→0,从而D,→∞这显然是荒谬的,瑞利之后,金斯作过各种 努力,他发现,只要坚持经典的统计理论,这一荒谬结论就不可避免。历史上被人们称为 紫外灾难
T c f c T c f T T 5 5 , 3 , 或 d c d c 2 其中 f ,f 的函数形式尚不能完全确定,利用上式可得下列两条定律(1893 年) (1)黑体的辐出度与绝对温度 T 的四次方成正比。即: 4 , 0 0 (T) T d T 8 2 4 5.67 10 W / m k 是一个普适常数 (1879 年斯忒藩从实验观察到,1884 年玻尔兹曼从理论上给出上式称为斯忒藩—玻 尔兹曼定律。) (2)任何温度下, ,T 都有一极大值,令这极大值对应的波长为 M ,则 b b m k mT 2.89 10 . 3 这个规律称为维恩位移定律。 三、维恩公式和瑞利—金斯公式 单纯从热力学原理出发,而不对辐射机制作任何具体的假设是不能将 f 和 f 的函数形 式进一步具体化的,历史上在这个问题获得最终的正确答案之前,有过下列两个公式,它 们对揭露经典物理的矛盾起了重大的作用。 (1)1896 年,维恩假设气体分子辐射的频率 只是与其速度 有关(这一假设看来 是没有什么根据的),从而得到与麦克斯韦速度分布律形式很相似的公式。 T T e c a / 2 3 ( , ) T c T e c 5 2 , , 为常数,上式称为维恩公式。 (2)瑞利—金斯定律 1900 年瑞利与金斯试图把能量均分定律应用到电磁辐射能量密度按频率颁的情况中, 他们假设空腔处于热平衡时的辐射场将是一些驻波,根据能量均分定理,每一列驻波斯湾 平均能量 kT ,与频率无关,这样可以算出 kT c T 2 , 2 2 或 kT c ,T 4 2 上式称为瑞利—金斯公式。 两公式都符合普遍形式。 同实验数据比较,在短波区域维恩公式符合的很好,但在长波范围则有虽不太大但却 是系统的偏离。瑞利公式与之相反,在长波部分符合的很好,但在短波波段偏离非常大, 不仅如此: 0, ,T ,从而T 这显然是荒谬的,瑞利之后,金斯作过各种 努力,他发现,只要坚持经典的统计理论,这一荒谬结论就不可避免。历史上被人们称为 紫外灾难

§7一3普朗克公式和能量子假说 正确的黑体辐射公式是普朗克给出的(1900年) R是玻尔兹曼常数,方=6.62×10~4Js为一普适常数,称为普朗克常数。普朗克公 式也符合普遍形式。 对于短波,市v>kTer灯>1化为维恩公式 对于长波,方v<kTer缸=1+方v/kT化为瑞一金公式在所有的波段里,普式 和实验符合的很好。 普式的得来,起初是半径验的,即利用内插法将适用于短波的维恩公式和适用于长波 瑞利一金斯公式衔接起来,在得到上述公式之后,普朗克才设法从理论上去论证它。 为了推导简单,选择由大量包含各种因有频率的谐振子组成的系统。通过发射和吸 收,谐振子与辐射场交换能量。仔细计算辐射场与谐振子之间的能量交换,得黑体的色辐 出度为 2 这里)是频率为v的谐振子在温度为T的平衡态中能量的平均值 下在我们来计算云,·在热平衡态中能量£的几率正比于灯(玻尔兹曼正则分布), 按照经典物理学的观念,谐振子的能量ε在0到©间连续取值,从而 广ee灯ds 8n= kT eds 得到的就是导致紫外灾难的瑞利一金斯公式。为了摆脱困难,普朗克提出如下一个非同寻 常的假设,谐振子能量的值只取某个基本单元的整数倍,即: 8=0,8o,280,380. 这样一来 ∑n,em 8v.n=1 利用等比级数的求和公式,可得
§7—3 普朗克公式和能量子假说 正确的黑体辐射公式是普朗克给出的(1900 年) 1 2 / 3 , 2 T kT c e 或 1 2 1 5 / 2 , T c kT e c R 是玻尔兹曼常数, J s 34 6.62 10 为一普适常数,称为普朗克常数。普朗克公 式也符合普遍形式。 对于短波, kT 1 / kT e 化为维恩公式 对于长波, kT e kT kT 1 / / 化为瑞—金公式在所有的波段里,普式 和实验符合的很好。 普式的得来,起初是半径验的,即利用内插法将适用于短波的维恩公式和适用于长波 瑞利—金斯公式衔接起来,在得到上述公式之后,普朗克才设法从理论上去论证它。 为了推导简单,选择由大量包含各种因有频率 的谐振子组成的系统。通过发射和吸 收,谐振子与辐射场交换能量。仔细计算辐射场与谐振子之间的能量交换,得黑体的色辐 出度为 2 ( , ) 2 , 2 T T c 这里 ( ,T ) ,是频率为 的谐振子在温度为 T 的平衡态中能量的平均值。 下在我们来计算 ,T 。在热平衡态中能量 的几率正比于 kT e / (玻尔兹曼正则分布), 按照经典物理学的观念,谐振子的能量 在 0 到∞间连续取值,从而 kT e d e d kT kT T / 0 / 0 ( , ) 得到的就是导致紫外灾难的瑞利—金斯公式。为了摆脱困难,普朗克提出如下一个非同寻 常的假设,谐振子能量的值只取某个基本单元 0 的整数倍,即: 0, 0 ,2 0 ,3 0 这样一来 kT e e n e n n n n kT n n kT T 1 ln 2 2 0 0 / 0 / 0 ( , ) 0 0 0 利用等比级数的求和公式,可得