
第三章几何光学的基本原理 在波面线度远较波长为大时,研究光的反射,折射成象等问题,如果不用波长、位相 等波动概念,而代之以光线和波面等概念,并用几何的方法来研究,将更为方便。 §3一1光线的概念 一、光线与波面 “光线”只能表示光的传播方向,决不可认为是从实际光束中借助于有孔光闲分出 个狭窄部分。只有在R>入的极限情况下,光的传播过程才用不者以次波叠加原理来分析, 而只用光线表示光的传播方向。我们说“光束由无数光线构成”,不过是说光沿无数不同的 方位传播罢了 在各向同性介质中,光的传播方向总是和波面的法线方向相重合。在许多实际情况下, 人们经常考虑的只是光的传播方向问题,可以不去考虑位相。这时被面就只是垂直于光线的 几何平面或曲面。这种极限情况,实际上是把光线和波面都看作是抽象的数学概念。对许多 实际问颗,借助于光线的概念,应用某些基本的实验定律及几何定律,就可以讲行一切必要 的计算而不必涉及光的本性问题。这部分以儿何定律和某些基本实验定律为基础的光学称为 几何光学。 第一、二章波动光学中主要考虑的是波长、振幅和位相,这一章所考虑的主要是光线 和波面。几何光学所研究的实际上就是波动光学的极限情况。 二、几何光学的基本实验定律 (1)光在均匀介质中的直线传播定律。 (2)光通过两种介质分界面时的反射和折射定律。 (3)光的独立传播定律和光路可逆定律。 §32费马原理 费马原理:光在指定的两点间传播,实际的光程总是一个极值。也就是说,光沿光程值 为最小、最大或恒定的路程传播。 图3-1
第三章 几何光学的基本原理 在波面线度远较波长为大时,研究光的反射,折射成象等问题,如果不用波长、位相 等波动概念,而代之以光线和波面等概念,并用几何的方法来研究,将更为方便。 §3—1 光线的概念 一、光线与波面 “光线”只能表示光的传播方向,决不可认为是从实际光束中借助于有孔光阑分出一 个狭窄部分。只有在 R 的极限情况下,光的传播过程才用不着以次波叠加原理来分析, 而只用光线表示光的传播方向。我们说“光束由无数光线构成”,不过是说光沿无数不同的 方位传播罢了。 在各向同性介质中,光的传播方向总是和波面的法线方向相重合。在许多实际情况下, 人们经常考虑的只是光的传播方向问题,可以不去考虑位相。这时波面就只是垂直于光线的 几何平面或曲面。这种极限情况,实际上是把光线和波面都看作是抽象的数学概念。对许多 实际问题,借助于光线的概念,应用某些基本的实验定律及几何定律,就可以进行一切必要 的计算而不必涉及光的本性问题。这部分以几何定律和某些基本实验定律为基础的光学称为 几何光学。 第一、二章波动光学中主要考虑的是波长、振幅和位相,这一章所考虑的主要是光线 和波面。几何光学所研究的实际上就是波动光学的极限情况。 二、几何光学的基本实验定律 (1)光在均匀介质中的直线传播定律。 (2)光通过两种介质分界面时的反射和折射定律。 (3)光的独立传播定律和光路可逆定律。 §3—2 费马原理 费马原理:光在指定的两点间传播,实际的光程总是一个极值。也就是说,光沿光程值 为最小、最大或恒定的路程传播。 图 3-1

光在均匀介质中直线传播。反射和折射定律都是费马原理的必然结果。 图3.2 CC”垂直平面1,则:AC'>AC”C'B>C"B。因此折射点必在O0上入射面 和折射面在同一平面内。 设:A(x,y)。 B:(x2,y2),C:(x,0)X1<x<x2 则:6=n,AC+n,CB=n1Vx-x)2+y+n2Vx,-x)2+明 d6 n(x-x) n2(32-x 本x-x矿+ x2-x)+ =乃4r℃n,Cg CB =(m sini-n siniz)=0 nsin=nsiniz 同样能证明反射定律。 §3一3单心光束、实象和虚象 一、单心光束、实象和虚象 如果仅考虑光束的传播方向而不讨论其它问题,那么一个光束可以看成是由许多光线 构成的。根据这个概念可以把发光点看做是一个发散光束的顶点,凡是具有单个顶点的光束 叫做单心光束。如果在反射或折射之后光线的方向虽然改变了,但光束中仍然能找到一个顶 点P',也就是说光束的单心性没有道到破坏,那么这个顶点P'便是发光点P的象。在这种 情况下,每个发光点都给出一个和它对应的象点。如果光束中各光线实际上确是在该点会聚 的,那么这个聚点叫做实象。如果反射或折射后的光束仍是发散的,但是把这些光线反向沿 长后仍能找到光束的顶点,则光束仍保持单心性。这个发散光束的会聚点叫做虚象。 二、实物、实象、虚象的联系与区别
光在均匀介质中直线传播。反射和折射定律都是费马原理的必然结果。 图 3-2 CC垂直平面 1,则: AC AC CB CB 。因此折射点必在OO上入射面 和折射面在同一平面内。 设: 1 1 2 2 1 2 A:(x , y ), B :(x , y ), C :(x,0) x x x 则: 2 2 2 2 2 2 1 2 1 2 1 1 n AC n CB n (x x ) y n (x x) y 1 1 2 2 1 1 2 2 1 2 2 2 2 2 2 2 2 1 2 1 1 1 sin sin ( sin sin ) 0 ( ) ( ) ( ) ( ) n i n i n i n i CB n CB AC n A C x x y n x x x x y n x x dx d 同样能证明反射定律。 §3—3 单心光束、实象和虚象 一、单心光束、实象和虚象 如果仅考虑光束的传播方向而不讨论其它问题,那么一个光束可以看成是由许多光线 构成的。根据这个概念可以把发光点看做是一个发散光束的顶点,凡是具有单个顶点的光束 叫做单心光束。如果在反射或折射之后光线的方向虽然改变了,但光束中仍然能找到一个顶 点 P ,也就是说光束的单心性没有遭到破坏,那么这个顶点 P 便是发光点 P 的象。在这种 情况下,每个发光点都给出一个和它对应的象点。如果光束中各光线实际上确是在该点会聚 的,那么这个聚点叫做实象。如果反射或折射后的光束仍是发散的,但是把这些光线反向沿 长后仍能找到光束的顶点,则光束仍保持单心性。这个发散光束的会聚点叫做虚象。 二、实物、实象、虚象的联系与区别
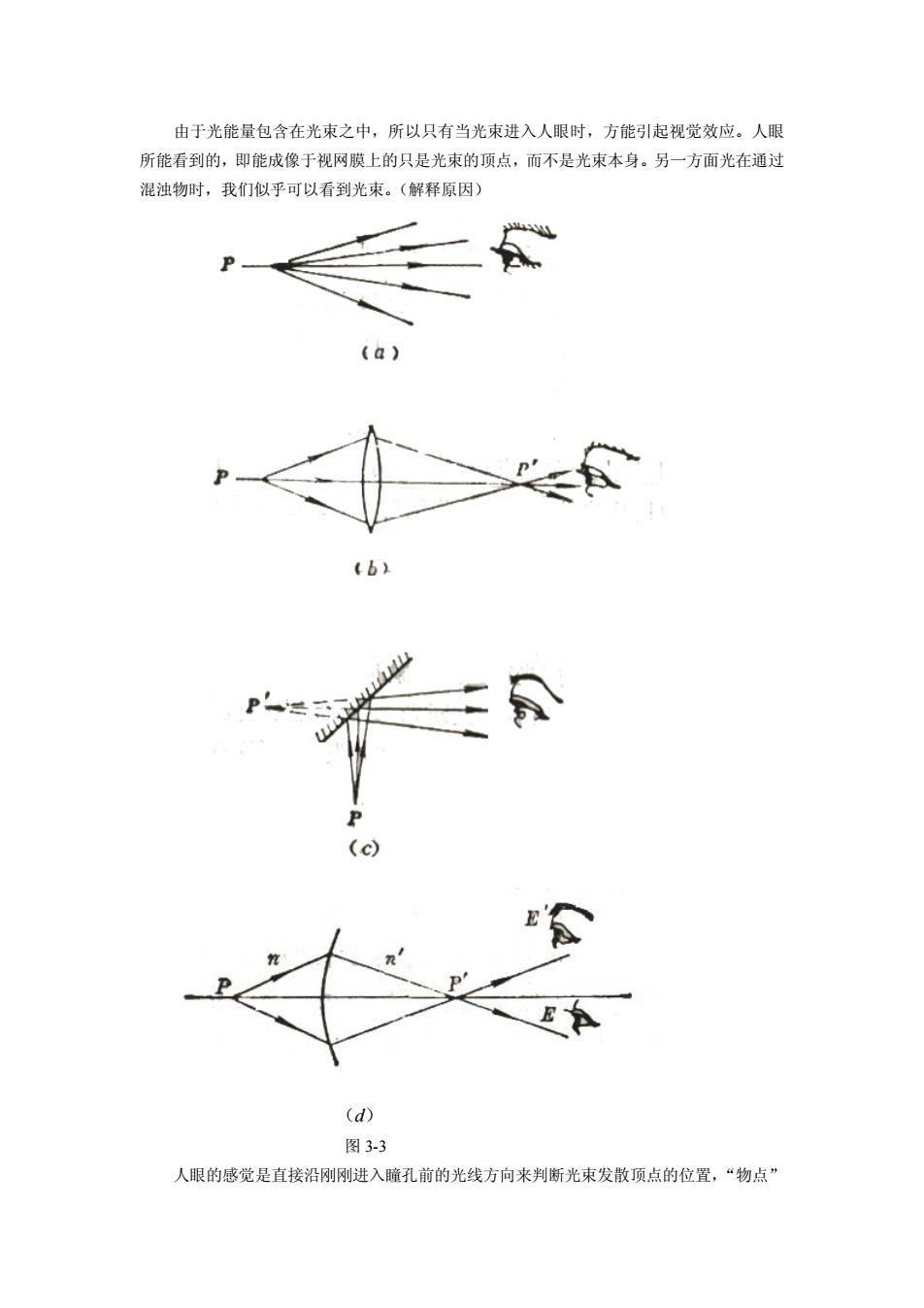
由于光能量包含在光束之中,所以只有当光束进入人眼时,方能引起视觉效应。人眼 所能看到的,即能成像于视网膜上的只是光束的顶点,而不是光束本身。另一方面光在通过 混浊物时,我们似乎可以看到光束。(解释原因) (d) 图3-3 人眼的感觉是直接沿刚刚进入瞳孔前的光线方向来判断光束发散顶点的位置,“物点
由于光能量包含在光束之中,所以只有当光束进入人眼时,方能引起视觉效应。人眼 所能看到的,即能成像于视网膜上的只是光束的顶点,而不是光束本身。另一方面光在通过 混浊物时,我们似乎可以看到光束。(解释原因) (d) 图 3-3 人眼的感觉是直接沿刚刚进入瞳孔前的光线方向来判断光束发散顶点的位置,“物点
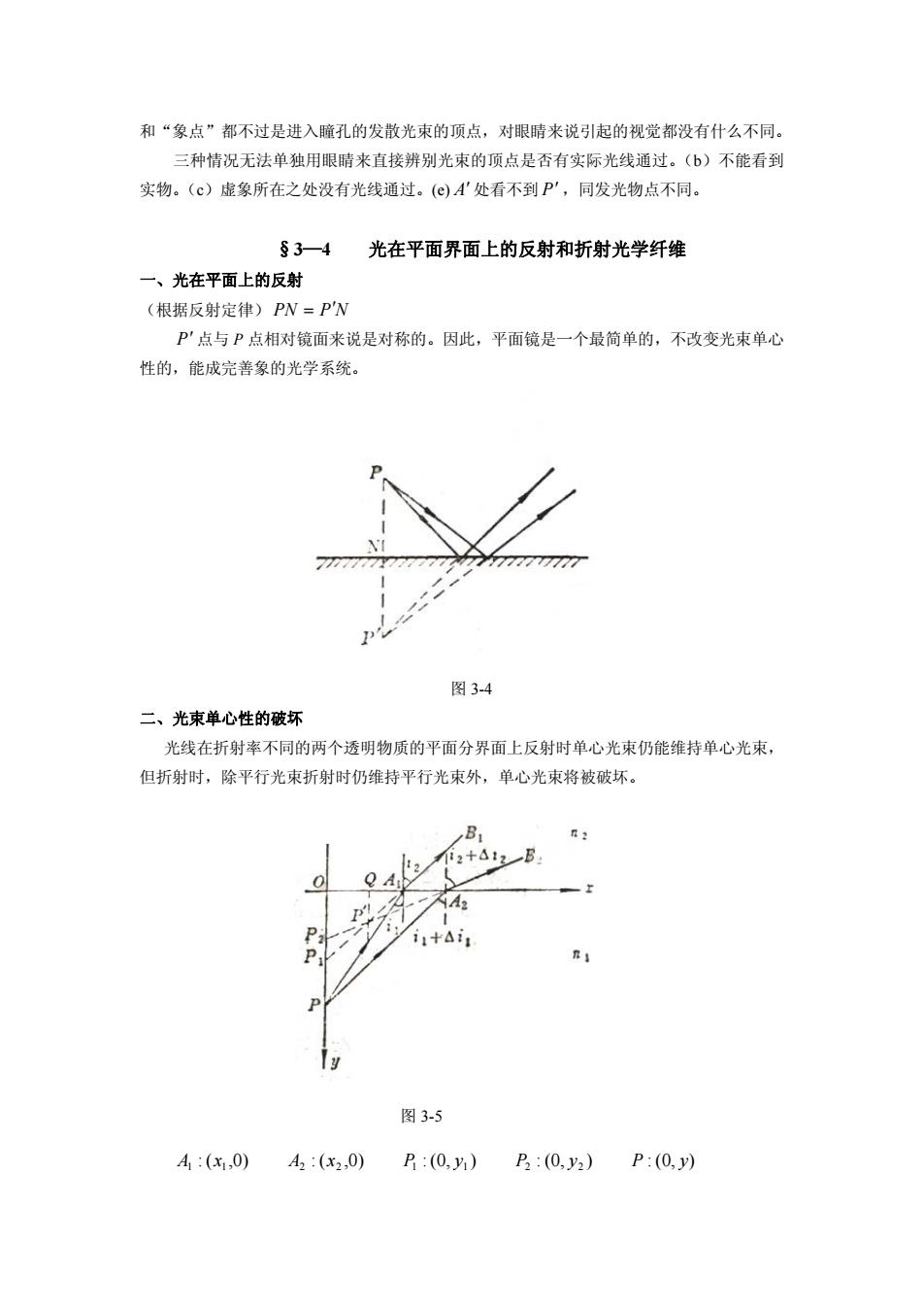
和“象点”都不过是进入瞳孔的发散光束的项点,对眼晴来说引起的视觉都没有什么不同。 三种情况无法单独用眼睛来直接辨别光束的顶点是否有实际光线通过。(b)不能看到 实物。(c)虚象所在之处没有光线通过。()A'处看不到P',同发光物点不同. §3-4 光在平面界面上的反射和折射光学纤维 一、光在平面上的反射 (根据反射定律)PN=P'N P'点与P点相对镜面来说是对称的。因此,平面镜是一个最简单的,不改变光束单心 性的,能成完善象的光学系统。 图34 二、光束单心性的破坏 光线在折射率不同的两个透明物质的平面分界面上反射时单心光束仍能维持单心光束, 但折射时,除平行光束折射时仍维持平行光束外,单心光束将被破坏。 B 2+△12B: 图3-5 4:(x1,0) A2:(x2,0) P:(0,y)
和“象点”都不过是进入瞳孔的发散光束的顶点,对眼睛来说引起的视觉都没有什么不同。 三种情况无法单独用眼睛来直接辨别光束的顶点是否有实际光线通过。(b)不能看到 实物。(c)虚象所在之处没有光线通过。(e) A 处看不到 P ,同发光物点不同。 §3—4 光在平面界面上的反射和折射光学纤维 一、光在平面上的反射 (根据反射定律) PN PN P 点与 P 点相对镜面来说是对称的。因此,平面镜是一个最简单的,不改变光束单心 性的,能成完善象的光学系统。 图 3-4 二、光束单心性的破坏 光线在折射率不同的两个透明物质的平面分界面上反射时单心光束仍能维持单心光束, 但折射时,除平行光束折射时仍维持平行光束外,单心光束将被破坏。 图 3-5 : ( ,0) : ( ,0) : (0, ) : (0, ) : (0, ) 1 1 2 2 1 1 2 2 A x A x P y P y P y
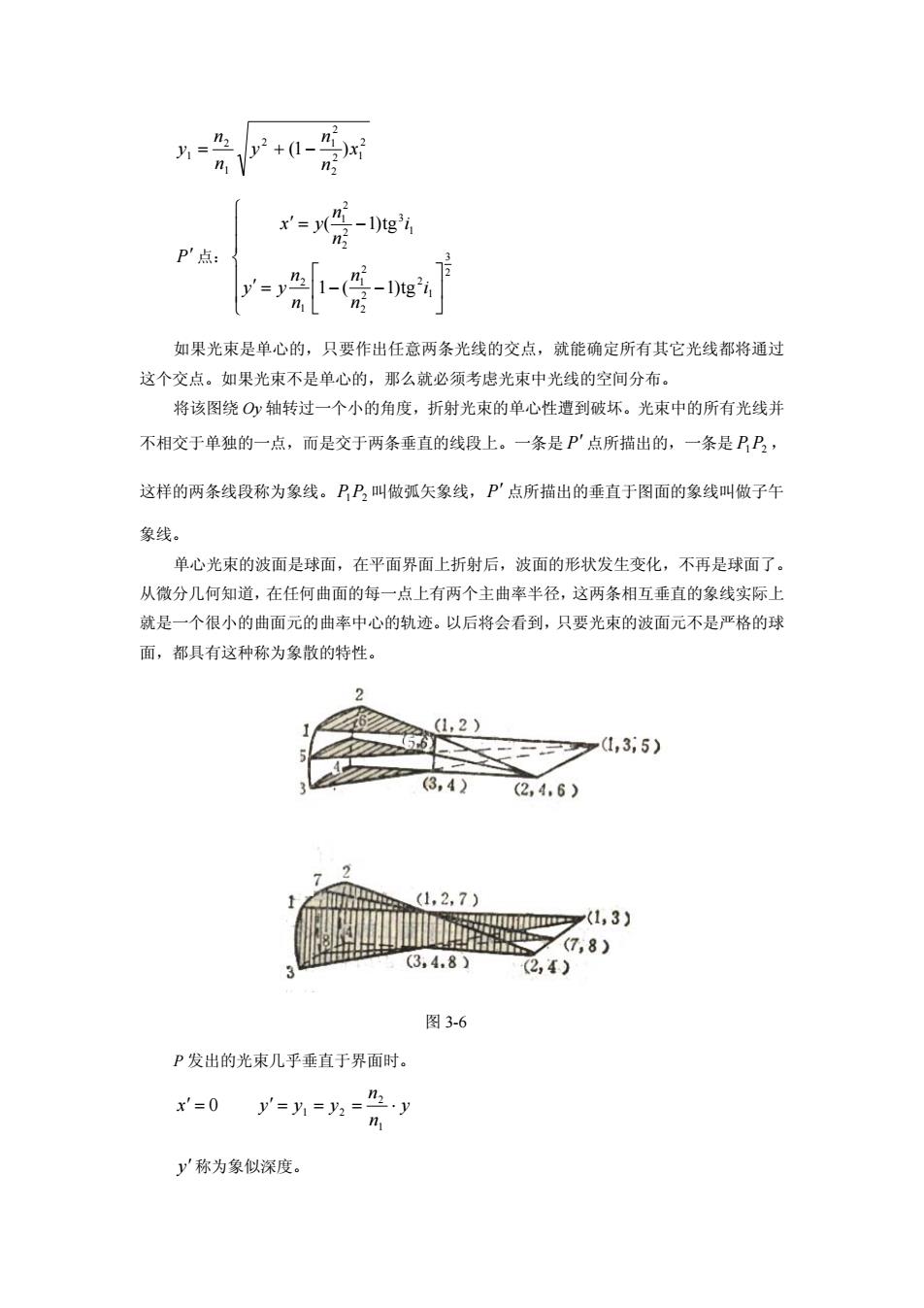
P'点: -e m 如果光束是单心的,只要作出任意两条光线的交点,就能确定所有其它光线都将通过 这个交点。如果光束不是单心的,那么就必须考虑光束中光线的空间分布。 将该图绕O轴转过一个小的角度,折射光束的单心性遭到破坏。光束中的所有光线并 不相交于单独的一点,而是交于两条垂直的线段上。一条是P点所描出的,一条是乃B, 这样的两条线段称为象线。PP,叫做弧矢象线,P'点所描出的垂直于图面的象线叫做子午 象线。 单心光束的波面是球面,在平面界面上折射后,波面的形状发生变化,不再是球面了。 从微分几何知道,在任何曲面的每一点上有两个主曲率半径,这两条相互垂直的象线实际上 就是一个很小的曲面元的曲率中心的轨迹。以后将会看到,只要光束的波面元不是严格的球 面,都具有这种称为象散的特性。 ,2) 三2y1,35) (3,4) (24,6) (1,2,7) 00y(1,3) (7,8) 3,4,8) 2,4) 图3-6 P发出的光束几乎垂直于界面时。 x'=0 y=男==y y'称为象似深度
2 2 1 2 2 2 1 1 2 1 (1 )x n n y n n y P 点: 2 3 1 2 2 2 2 1 1 2 1 3 2 2 2 1 1 ( 1)tg ( 1)tg i n n n n y y i n n x y 如果光束是单心的,只要作出任意两条光线的交点,就能确定所有其它光线都将通过 这个交点。如果光束不是单心的,那么就必须考虑光束中光线的空间分布。 将该图绕 Oy 轴转过一个小的角度,折射光束的单心性遭到破坏。光束中的所有光线并 不相交于单独的一点,而是交于两条垂直的线段上。一条是 P 点所描出的,一条是 P1P2 , 这样的两条线段称为象线。P1P2 叫做弧矢象线,P 点所描出的垂直于图面的象线叫做子午 象线。 单心光束的波面是球面,在平面界面上折射后,波面的形状发生变化,不再是球面了。 从微分几何知道,在任何曲面的每一点上有两个主曲率半径,这两条相互垂直的象线实际上 就是一个很小的曲面元的曲率中心的轨迹。以后将会看到,只要光束的波面元不是严格的球 面,都具有这种称为象散的特性。 图 3-6 P 发出的光束几乎垂直于界面时。 y n n x y y y 1 2 1 2 0 y 称为象似深度