《光学》课程授课教案（讲义）光的偏振

光学第五章光的偏振 第五章 光的偏振 §5.1光的偏振态 偏振：振动方向相对于传播方向的不对称性。 一.光是横波 1、光是电磁波—横波 2、用二向色性晶体（电气石晶体、硫酸碘奎宁晶体）检验一一横波。 最初的器件是用细导线做成的密排线桶（金质线栅，5.08×10），光通过时，由于 与导线同方向的电场被吸收，留下与其垂直的振动。 1928年，Harvaed大学的Land(19岁)发明了人造偏振片，用聚乙烯醇膜浸碘制得。 到1938年，出现了H型偏振片，原理相同。 3、 起偏：使光变为具有偏振特性。 检偏：检验光的偏振特性。 透振方向：通过偏振仪器光的电矢量的振动方向。 二.光的偏振态 偏振：振动方向相对于传播方向的不对称性 对可见光，只考虑其电矢量。 1.自然光 振动方向随机，相对于波矢对称。光的叠加是按强度相加。 可沿任章方向正交分解，在在一方向的强度为总强度之半，1=)。 自然光是大量原子同时发出的光波的集合。其中的每一列是由一个原子发出的，有一个 偏振方向和相位，但光波之间是没有任何关系的。所以，他们的集合，就是在各个方向振动 相等、相位差随机的自然光

光学 第五章 光的偏振 第五章 光的偏振 § 5.1 光的偏振态 偏振：振动方向相对于传播方向的不对称性。 一．光是横波 1、 光是电磁波——横波 2、 用二向色性晶体（电气石晶体、硫酸碘奎宁晶体）检验——横波。 最初的器件是用细导线做成的密排线栅（金质线栅，d=5.08×10-4mm），光通过时，由于 与导线同方向的电场被吸收，留下与其垂直的振动。 1928 年，Harvaed 大学的 Land（19 岁）发明了人造偏振片，用聚乙烯醇膜浸碘制得。 到 1938 年，出现了 H 型偏振片，原理相同。 3、名词 起偏：使光变为具有偏振特性。 检偏：检验光的偏振特性。 透振方向：通过偏振仪器光的电矢量的振动方向。 二．光的偏振态 偏振：振动方向相对于传播方向的不对称性。 对可见光，只考虑其电矢量。 1．自然光 振动方向随机，相对于波矢对称。光的叠加是按强度相加。 可沿任意方向正交分解，在任一方向的强度为总强度之半。 0 2 1  II 自然光是大量原子同时发出的光波的集合。其中的每一列是由一个原子发出的，有一个 偏振方向和相位，但光波之间是没有任何关系的。所以，他们的集合，就是在各个方向振动 相等、相位差随机的自然光。 1

光学第五章光的偏振 y 在直角坐标系中，一列沿z向传播、振动方向与X轴夹角为日的光，在X方向的振幅 为4=Acos@,由于各个光波在X方向的总强度是光强相加，故有 1.=(4)d0=Acos2au0=z4 同理1，=π 而总光强1=d0=2,故1，=，=。 2.平面偏振光（线偏振光） 只包含单一振动方向的电矢量。 在任一方向的光强1。=1。cos20,马吕斯定律。 用偏振片可以获得平面偏振光， 偏振仪器（起偏器）的消光比=最小透射光强最大透射光强 3.部分偏振光 介于自然光和线偏光之间。 偏振度=(IMAx-IMN)/(IMAx+HIN) 4.圆偏振光 电矢最端点轨迹的投影为圆。 其电矢量不是沿某一方向作周期性振动，而是做匀速旋转。但其电矢量的投影则是简谐 振动

光学 第五章 光的偏振 在直角坐标系中，一列沿 z 向传播、振动方向与 X 轴夹角为θ的光，在 X 方向的振幅 为  ，由于各个光波在 X 方向的总强度是光强相加，故有  AA cos x  2 2 0 22 2 2 0 )( cos AdAdAI x x          同理 2 AI y   而总光强 ，故 2 2 0 2 2 AdAI     0 2 1 III yx  2．平面偏振光（线偏振光） 只包含单一振动方向的电矢量。 在任一方向的光强   ，马吕斯定律。 2 0  II cos 用偏振片可以获得平面偏振光。 偏振仪器（起偏器）的消光比=最小透射光强/最大透射光强 3．部分偏振光 介于自然光和线偏光之间。 偏振度=（IMAX-IMIN）/（IMAX+IMIN） 4．圆偏振光 电矢量端点轨迹的投影为圆。 其电矢量不是沿某一方向作周期性振动，而是做匀速旋转。但其电矢量的投影则是简谐 振动。 2

光学第五章光的偏振 E(t1 t1 t2 每一时刻的电矢量可以分解为振幅相等、相位差为2、相互垂直的振动 [E,(t)=Acos(ot-k) 0=-，右旋 E,(t)=Acos(ot-k-A) ，迎者光的传播方向观察。 +号左旋 E(t)=E,E,=Acos(@t-k)+Acos(-) 用偏振片检验，圆偏光与自然光相同 5.椭圆偏振 电矢量端点轨迹的投影为椭圆。每一时刻的电矢量可分解为 [E,=A,cos(at-k) E2E,E cos=sinA E=4cosa-e-Ao三元+EA,A E,）=E,天+E,=Acos(o-ke)+Acos(-k-△p) 椭圆长轴或短轴与坐标轴的夹角g20= 24,4, 42-有os40 可以容易得到电矢量的戴转方向，即Ap∈1，L,左旋 △p∈Ⅲ，IN,右旋

光学 第五章 光的偏振 每一时刻的电矢量可以分解为振幅相等、相位差为π/2、相互垂直的振动。      cos()( ) )cos()(   kztAtE kztAtE y x          ，左旋 ，右旋 2 2     ，迎着光的传播方向观察。 yx ykztAxkztAyExEztE     ) 2 ),( cos()cos(     用偏振片检验，圆偏光与自然光相同。 5．椭圆偏振光 电矢量端点轨迹的投影为椭圆。每一时刻的电矢量可分解为        cos( ) )cos(    kztAE kztAE yy xx     2 2 2 2 2 sincos 2 yx yx y y x x AA EE A E A E yx x y ykztAxkztAyExEztE     ),(    cos()cos(   ) 椭圆长轴或短轴与坐标轴的夹角     cos 2 2 22 yx yx AA AA tg 可以容易得到电矢量的旋转方向，即      右旋 左旋 , , IVIII III   3

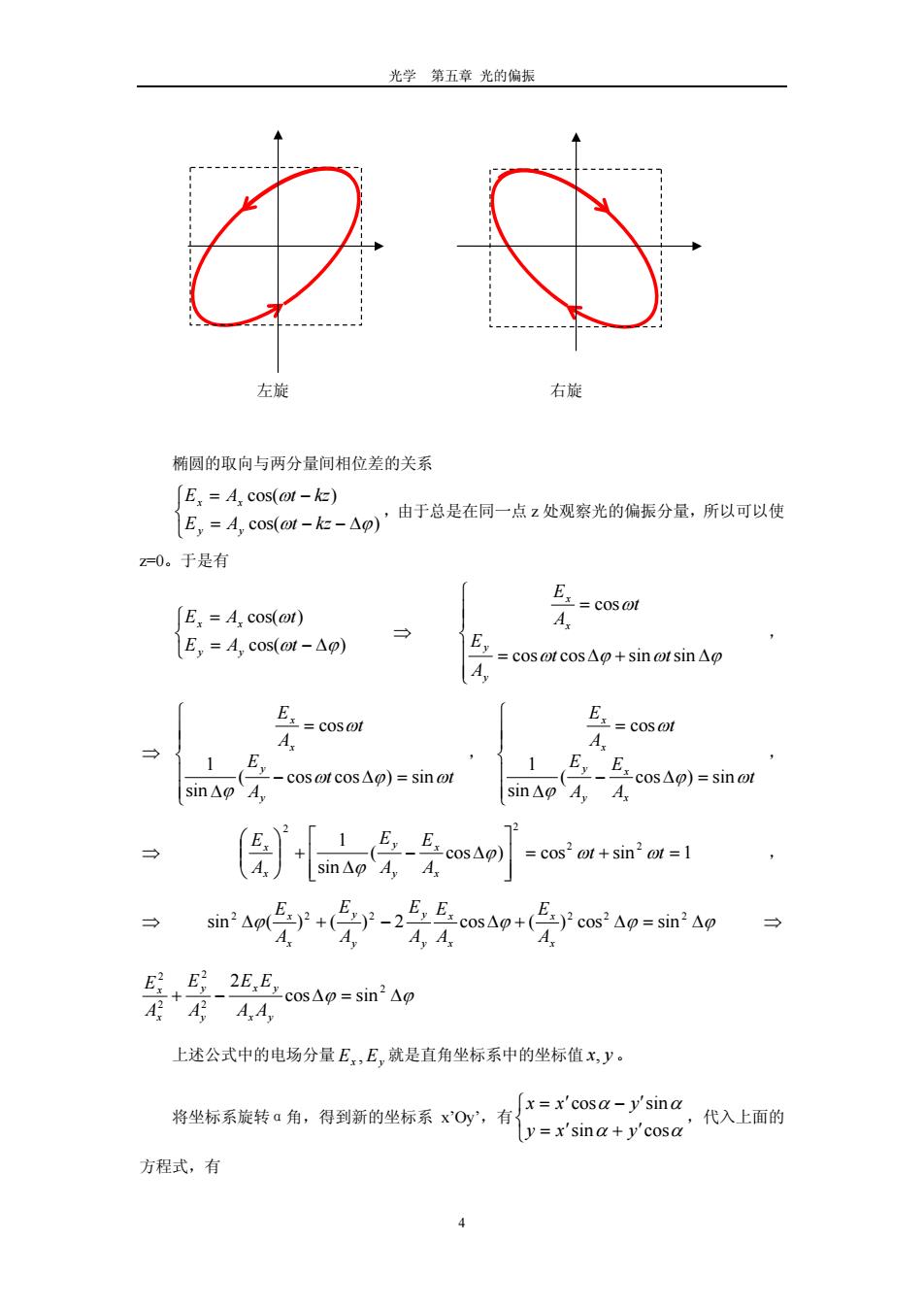
光学第五章光的偏振 右旋 椭圆的取向与两分量间相位差的关系 [E =A,cos(oot-k=) E,=4,c0s(0W-E-Ap由于总是在同一点z处观察光的偏振分量，所以可以使 x0。于是有 E,=A,cos(ot) A. 1E,=A,cos(am-△o) =cos @t cos△g+sin@tsin△p A E, E.=cosot A 1 1 Ey E sin Ao A. -cos@t cos.△p)=sinot sin△pA,A cos△p)=sinot aa气气-异经mAp.党owa0ma如 E，E_2E,c0=sim2Ap 上述公式中的电场分量E,E,就是直角坐标系中的坐标值x,y。 将坐标系旋转a角，得到箭的坐标系Oy,有：=c0sa-ys加 ,代入上面的 y=x'sina+y'cosa 方程式，有

光学 第五章 光的偏振 左旋 右旋 椭圆的取向与两分量间相位差的关系        cos( ) )cos(    kztAE kztAE yy xx ，由于总是在同一点 z 处观察光的偏振分量，所以可以使 z=0。于是有               sinsincoscos cos t t A E t A E y y x x ，       cos( ) )cos(   tAE tAE yy xx           )    t t A E t A E y y x x    coscos( sin sin 1 cos ，           t A E A E t A E x x y y x x    ( sin)cos sin 1 cos ，  ( cos)cos 1sin sin 1 2 2 2 2                     tt A E A E A E x x x x     y y ，        2 2 2 22 2 )()(sin cos)(cos sin x x x x y y y y x x A E A E A E A E 2 A E      2 2 2 sincos 2 yx yx y y AA EE A E 2 2 x x A E 上述公式中的电场分量 , EE yx 就是直角坐标系中的坐标值 x, y 。 将坐标系旋转α角，得到新的坐标系 x’Oy’，有              sin cos cos sin yxy yxx ，代入上面的 方程式，有 4

光学第五章光的偏振 xcos'a-2x'ycosasina+ysin'axsin'a+2x'y'cosasina+ycosa A经 A cosncsn)-ycosasinsin A,A, 要使在新坐标系中得到正椭圆，即长轴、短轴沿坐标轴方向，只需要使得上式中xy的系数 为零即可。故有 2cosasina2cosasina_2(cosa-sinc A A.Ay -A2 cosasina+A:cosasina-A,A,(cos2a-sin'a)cosA=0 由于2 cosa sina=sin2a,cos2a-sin2a=cos2a,所以有 Gsn2a-Gsn2a)-44os2acs4p n2244p,即g2a2无-年 cos2a -A 。2A4c0s△P,由于椭圆的对称性，口的值在 子孕间即可。 新坐标系中，椭圆方程为 xcos2a+y2 sin'a x2 sin2a+y cos2a A sin2a-ysin2acsin A,A

光学 第五章 光的偏振                             2 2 2 2 2 2 22 22 2 22 22 sincos sincos (cos sincos)sin 2 sincos2cos sin sincos2sin cos yx x y AA x yx y A x yx y A x yx y 要使在新坐标系中得到正椭圆，即长轴、短轴沿坐标轴方向，只需要使得上式中 的系数 为零即可。故有 yx  0cos (cos2sincos2sincos2 )sin 2 2 2 2         Ax Ay AA yx  sincos sincos (cos 0cos)sin 2 2 2 2  Ay   Ax   AA yx    由于    2sinsincos2  ， 2cossincos  ，所以有 2 2    )2sin2sin(  cos2cos  2 1 2 2 Ax Ay AA yx 22 cos2 2cos 2sin yx yx AA AA       ，即 22 cos2 2 yx yx AA AA tg      ，由于椭圆的对称性， 的值在 ) 4 , 4 (    间即可。 新坐标系中，椭圆方程为                    2 2 2 2 22 22 2 22 22 sincos 2sin2sin cos sin sin cos yx x y AA x y A x y A x y 5