
p2=R2-(R-h)2=r2-G+) 2Rh-h2=2-6-2,h-h h=片-公 (3) 2(R+) 将(2)和(3)代入(1) k=pR+-D2L+昌 R 无R 如果用平行光照射圆孔,R→0则 p:=√k P点合振幅的大小取决于露出的带数k,而当被长及圆孔的位置和大小都给定时,k取 决于观察点P的位置,k为奇数相对应的那些点,合振幅A较大,与k为偶数相对应的那 些P点,A较小。这个结果很容易用实验来证实。 如果不用光阑,相当于圆孔的半径为无限大,账为无限小,此时P点的合振幅为 A。=号,即没有遮蔽的整个被面对P点的作用等于一个波带在该点的作用的一半,因为 波带的面积非常小.如:=5004,=1m。第一个波带的面积约为子mm2,半径约为 乞mm。所以没有遮道的整个波面的光能的传播。几乎可以看作沿OP直线进行,这也是 般把光视作直线传播的缘由。P点离开光源越远,:愈小,光强愈弱。在此情况下屏沿者对 称轴线前进时,不发生上述某些点较强某些点较弱的现象。 如果圆孔的半径具有一定的大小,观察点P的位置仅使波面上露出第一个带,则 A=a 与没有光阑时比较,振幅是二倍,光强则增加到四倍。所以光在通过圆孔以后到达任 一点时的光强,不能够单独由光源到该点的距离来决定,还取决于圆孔的位置及大小,只 当圆孔足够大,使号小到可以略去不计时,才和光的直线传播概念所推得的结果一致。 所有这些讨论都假定0是理想的点光源,但实际的光源都有一定的大小,光源的每点 各自产生它自己的衍射花样,它们是不相干的,光源的线度应小到使光源上某些点所产生 的亮条纹不致落到另外一些点所产生的暗条纹上去。否则由于不相干叠加,衍射花样就会 完全模糊了,通常情况不会产生衍射花样,正是由于这个缘故
2 0 2 0 2 2 2 0 2 2 2 2 2 2 ( ) ( ) Rh h r r r h h R R h r r h k k k 2( ) 0 2 0 2 R r r r h k (3) 将(2)和(3)代入(1) ) 1 1 ( ( ) ) ( ) (1 ( ) 0 2 0 0 2 0 0 0 0 0 0 0 0 0 2 2 r R r R R r k R r r R k R r r k r R r r k r k r k 如果用平行光照射圆孔, R 则 0 k r k P 点合振幅的大小取决于露出的带数 k,而当波长及圆孔的位置和大小都给定时,k 取 决于观察点 P 的位置,k 为奇数相对应的那些点,合振幅 Ak 较大,与 k 为偶数相对应的那 些 P 点,Ak 较小。这个结果很容易用实验来证实。 如果不用光阑,相当于圆孔的半径为无限大,ak为无限小,此时 P 点的合振幅为 2 1 a A ,即没有遮蔽的整个波面对 P 点的作用等于一个波带在该点的作用的一半,因为 波带的面积非常小。如:λ=5000Å,R=r0=1m。第一个波带的面积约为 2 4 3 mm ,半径约为 mm 2 1 。所以没有遮避的整个波面的光能的传播,几乎可以看作沿 OP 直线进行,这也是一 般把光视作直线传播的缘由。P 点离开光源越远,a 愈小,光强愈弱。在此情况下屏沿着对 称轴线前进时,不发生上述某些点较强某些点较弱的现象。 如果圆孔的半径具有一定的大小,观察点 P 的位置仅使波面上露出第一个带,则 A1=a1 与没有光阑时比较,振幅是二倍,光强则增加到四倍。所以光在通过圆孔以后到达任 一点时的光强,不能够单独由光源到该点的距离来决定,还取决于圆孔的位置及大小,只 当圆孔足够大,使 2 k a 小到可以略去不计时,才和光的直线传播概念所推得的结果一致。 所有这些讨论都假定 0 是理想的点光源,但实际的光源都有一定的大小,光源的每点 各自产生它自己的衍射花样,它们是不相干的,光源的线度应小到使光源上某些点所产生 的亮条纹不致落到另外一些点所产生的暗条纹上去。否则由于不相干叠加,衍射花样就会 完全模糊了,通常情况不会产生衍射花样,正是由于这个缘故
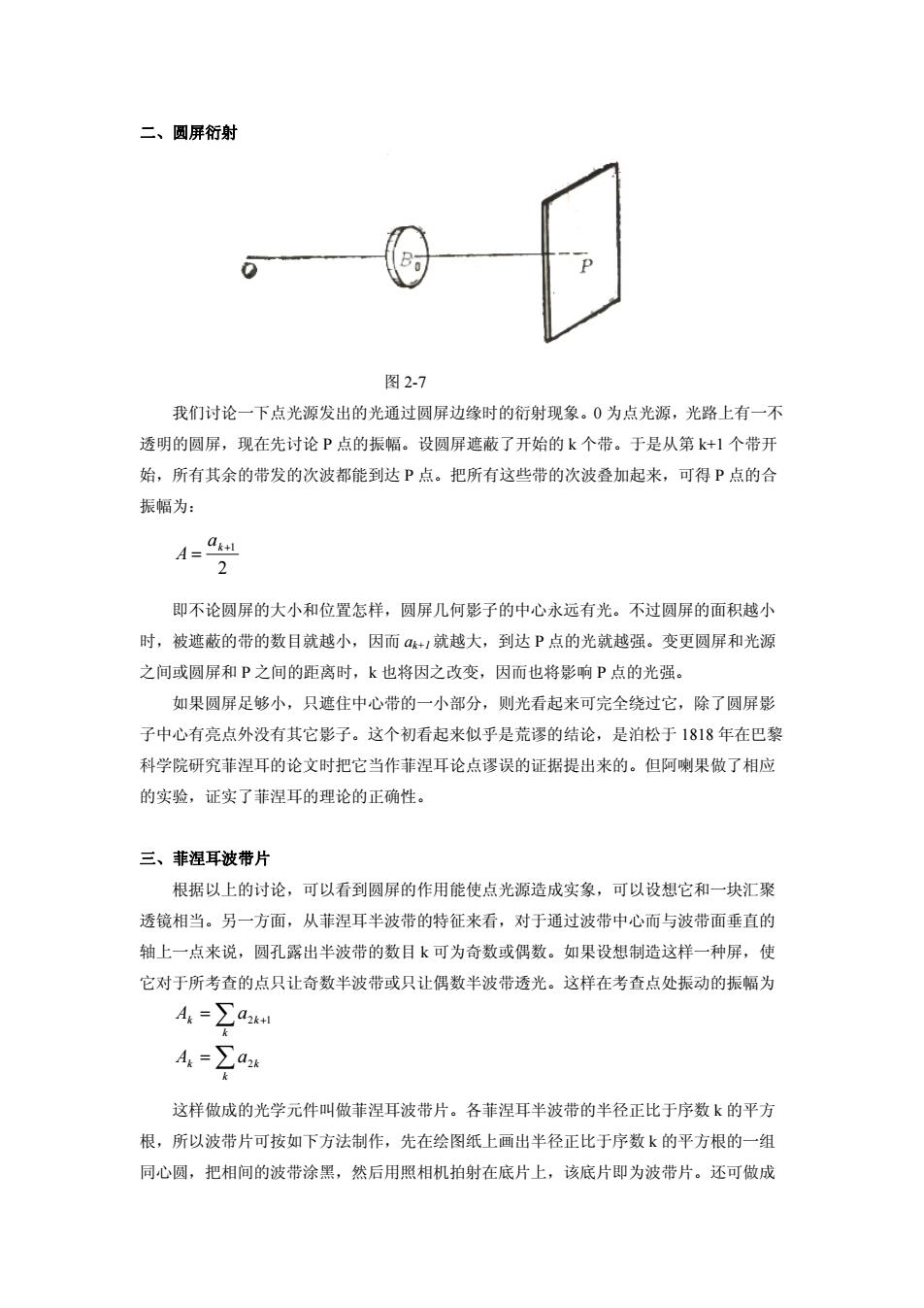
二、圆屏行射 图2-7 我们讨论一下点光源发出的光通过圆屏边缘时的衍射现象。·为点光源,光路上有一不 透明的圆屏,现在先讨论P点的振幅。设圆屏遮蔽了开始的k个带。于是从第k+1个带开 始,所有其余的带发的次波都能到达P点。把所有这些带的次波叠加起来,可得P点的合 振幅为: A=9 即不论圆屏的大小和位置怎样,圆屏几何影子的中心永远有光。不过圆屏的面积越小 时,被遮蔽的带的数目就越小,因而1就越大,到达P点的光就越强。变更圆屏和光源 之间或圆屏和P之间的距离时,k也将因之改变,因而也将影响P点的光强。 如果圆屏足够小,只遮住中心带的一小部分,则光看起来可完全绕过它,除了圆屏影 子中心有亮点外没有其它影子。这个初看起来似乎是荒谬的结论,是泊松于1818年在巴黎 科学院研究菲涅耳的论文时把它当作菲涅耳论点谬误的证据提出来的。但阿喇果做了相应 的实验,证实了菲涅耳的理论的正确性。 三、菲涅耳波带片 根据以上的讨论,可以看到圆屏的作用能使点光源造成实象,可以设想它和一块汇聚 透镜相当。另一方面,从菲涅耳半波带的特征来看,对于通过波带中心而与波带面垂直的 轴上一点来说,圆孔露出半波带的数目k可为奇数或偶数。如果设想制造这样一种屏,使 它对于所考查的点只让奇数半波带或只让偶数半波带透光。这样在考查点处振动的振幅为 A=∑a A=∑a2 这样做成的光学元件叫做菲涅耳波带片。各菲涅耳半波带的半径正比于序数k的平方 根,所以波带片可按如下方法制作,先在绘图纸上画出半径正比于序数k的平方根的一组 同心圆,把相间的波带涂黑,然后用照相机拍射在底片上,该底片即为波带片。还可做成
二、圆屏衍射 图 2-7 我们讨论一下点光源发出的光通过圆屏边缘时的衍射现象。0 为点光源,光路上有一不 透明的圆屏,现在先讨论 P 点的振幅。设圆屏遮蔽了开始的 k 个带。于是从第 k+1 个带开 始,所有其余的带发的次波都能到达 P 点。把所有这些带的次波叠加起来,可得 P 点的合 振幅为: 2 1 k a A 即不论圆屏的大小和位置怎样,圆屏几何影子的中心永远有光。不过圆屏的面积越小 时,被遮蔽的带的数目就越小,因而 ak+1 就越大,到达 P 点的光就越强。变更圆屏和光源 之间或圆屏和 P 之间的距离时,k 也将因之改变,因而也将影响 P 点的光强。 如果圆屏足够小,只遮住中心带的一小部分,则光看起来可完全绕过它,除了圆屏影 子中心有亮点外没有其它影子。这个初看起来似乎是荒谬的结论,是泊松于 1818 年在巴黎 科学院研究菲涅耳的论文时把它当作菲涅耳论点谬误的证据提出来的。但阿喇果做了相应 的实验,证实了菲涅耳的理论的正确性。 三、菲涅耳波带片 根据以上的讨论,可以看到圆屏的作用能使点光源造成实象,可以设想它和一块汇聚 透镜相当。另一方面,从菲涅耳半波带的特征来看,对于通过波带中心而与波带面垂直的 轴上一点来说,圆孔露出半波带的数目 k 可为奇数或偶数。如果设想制造这样一种屏,使 它对于所考查的点只让奇数半波带或只让偶数半波带透光。这样在考查点处振动的振幅为 k k k k k k A a A a 2 2 1 这样做成的光学元件叫做菲涅耳波带片。各菲涅耳半波带的半径正比于序数 k 的平方 根,所以波带片可按如下方法制作,先在绘图纸上画出半径正比于序数 k 的平方根的一组 同心圆,把相间的波带涂黑,然后用照相机拍射在底片上,该底片即为波带片。还可做成