《分析化学》课程教学课件（PPT讲稿）第六章 配位滴定-3/4

第六章配位滴定法 Complexmetric Titrations 6.1配位滴定中的滴定剂 6.2i 配位平衡常数 6.3副反应系数和条件稳定常数 6.4配位滴定法的基本原理 6.5准确滴定与分别滴定判别式 6.6配位滴定中酸度的控制 6.7提高配位滴定选择性的途径 6.8配位滴定方式及其应用

1 6.1 配位滴定中的滴定剂 6.2 配位平衡常数 6.3 副反应系数和条件稳定常数 6.4 配位滴定法的基本原理 6.5 准确滴定与分别滴定判别式 6.6 配位滴定中酸度的控制 6.7 提高配位滴定选择性的途径 6.8 配位滴定方式及其应用 第六章 配位滴定法 （Complexmetric Titrations）

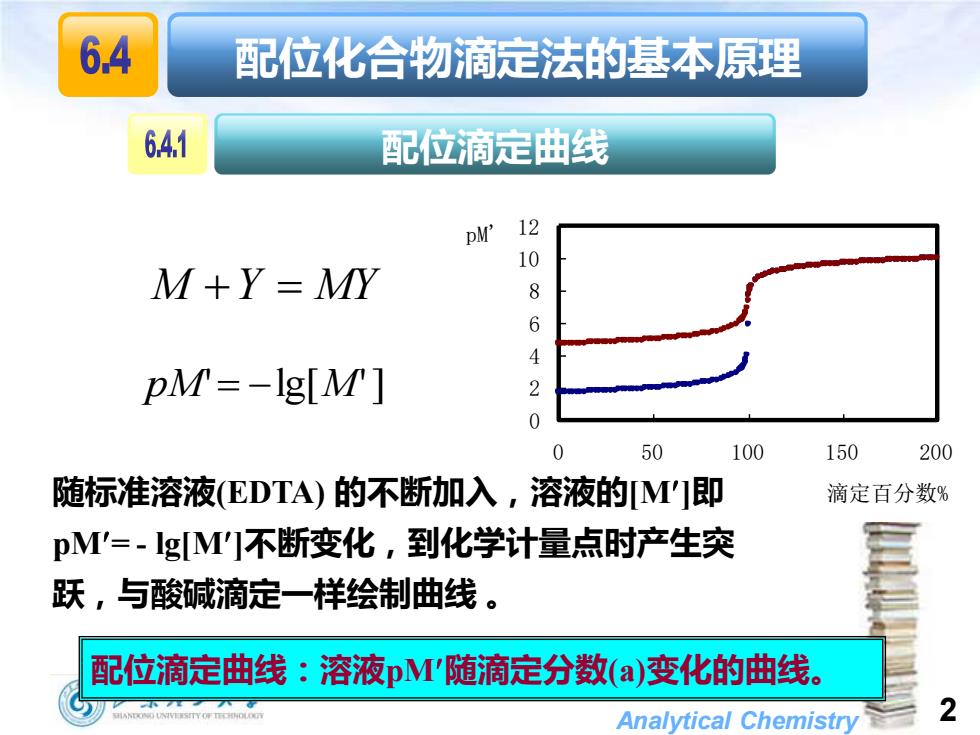
6.4 配位化合物滴定法的基本原理 641 配位滴定曲线 pM' 12 10 M+Y=MY 8 6 4 pM=-1g[M] 2 0 0 50 100 150 200 随标准溶液(EDTA)的不断加入，溶液的M'I即 滴定百分数% pM'=-gM门不断变化，到化学计量点时产生突 跃，与酸碱滴定一样绘制曲线。 配位滴定曲线：溶液pM'随滴定分数(a)变化的曲线。 Analytical Chemistry 2

Analytical Chemistry 2 pM' = −lg[M'] M +Y = MY 配位化合物滴定法的基本原理 配位滴定曲线 配位滴定曲线：溶液pM随滴定分数(a)变化的曲线。 0 2 4 6 8 10 12 0 50 100 150 200 滴定百分数% pM' 随标准溶液(EDTA) 的不断加入，溶液的[M]即 pM= - lg[M]不断变化，到化学计量点时产生突 跃，与酸碱滴定一样绘制曲线

[例刚pH=9.0,0.01000mol/L的EDTA滴定20.00mL, 0.01000mol/L的Zn2+(lgKz=16.5,pH=9.0,lgm-1.28, Iguzn(O-0.2） [解1 Ig K'ZnY=Ig KZny-Ig dzn-lg ay =15.02 1、滴定前 pZn'=-Ig[Zn']=-lg CZn =2.00 2、sp前 [Zn]=（c'zn-(cWy VZn+VY 加入19.98 ml EDTA pZn'=5.30 山东理子大军 Analytical Chemistry 3

Analytical Chemistry 3 [例] pH=9.0，0.01000mol/L的EDTA滴定20.00mL， 0.01000mol/L的Zn2+（ lgKZnY=16.5， pH=9.0， lgαY(H)=1.28, lgαZn(OH)=0.2 ） [解] lg K' ZnY = lg KZnY −lgZn −lg Y =15.02 1、滴定前 pZn'= −lg[Zn'] = −lgCZn = 2.00 2、sp前 Zn Y ( ) Zn ( ) Y [Zn'] V V cV cV + − = 加入19.98ml EDTA pZn =5.30

KZnY- [ZnY Isp 3、sp时 =1015.02 [Zn']sp[Y Isp [ZnY Isp≈c [Zn']sp=[Y'lsp 注：[Y门sp≠[Znsp Cp不等于原始浓度 cSp [Zn'Isp=K'znY p/ns'=()6.40 4、sp后： l天a0 [ZnY [ZnY]≈Czn- 0.01×20.00 加入20.02 ml EDTA 40.02 [Y]= 0.02×0.01 pZn'=12.02 少元2002 Analytical Chemistry

Analytical Chemistry 4 3、sp时 1 5.0 2 sp sp ' sp ZnY 10 [Zn'] [Y' ] [ZnY' ] K = = csp不等于原始浓度 (lg ' p ) 6.40 2 1 pZn ' sp sp ZnY Zn = K + c = sp sp Zn [ZnY' ]  c sp sp [Zn'] = [Y'] ZnY sp sp ' [Zn'] Zn K c = 注： sp sp [Y]  [Zn] 4、sp后： ' [Y' ] [ZnY' ] [Zn'] K ZnY = 加入20.02ml EDTA 40.02 0.01 20.00 [ZnY' ] Zn  C = 40.02 0.02 0.01 [Y' ]  = pZn =12. 02

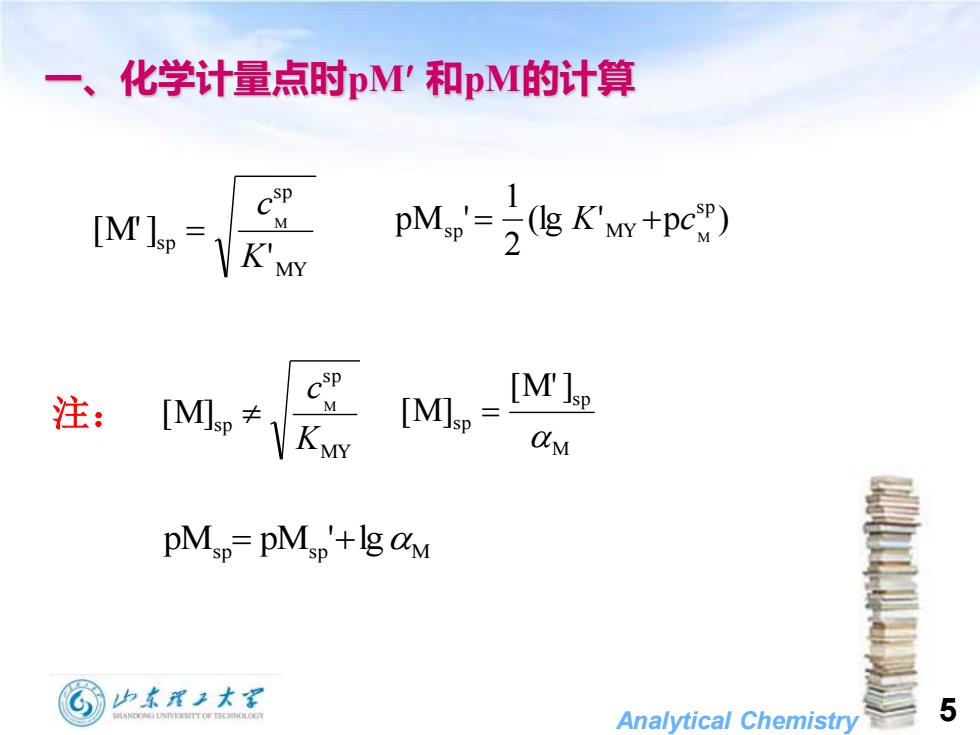
一、化学计量点时pM'和pM的计算 PM.(g K'v+pc) 注： [M≠KN CM [= M'p pMp=pMp'+lga必M 山东理工大军 Analytical Chemistry 5

Analytical Chemistry 5 一、化学计量点时pM 和pM的计算 (lg ' p ) 2 1 pM ' s p s p MY M = K + c MY sp sp ' [M'] M K c = 注： MY sp sp M] M [ K c  M sp sp [M'] [M]  = pMsp = pMsp '+lg M