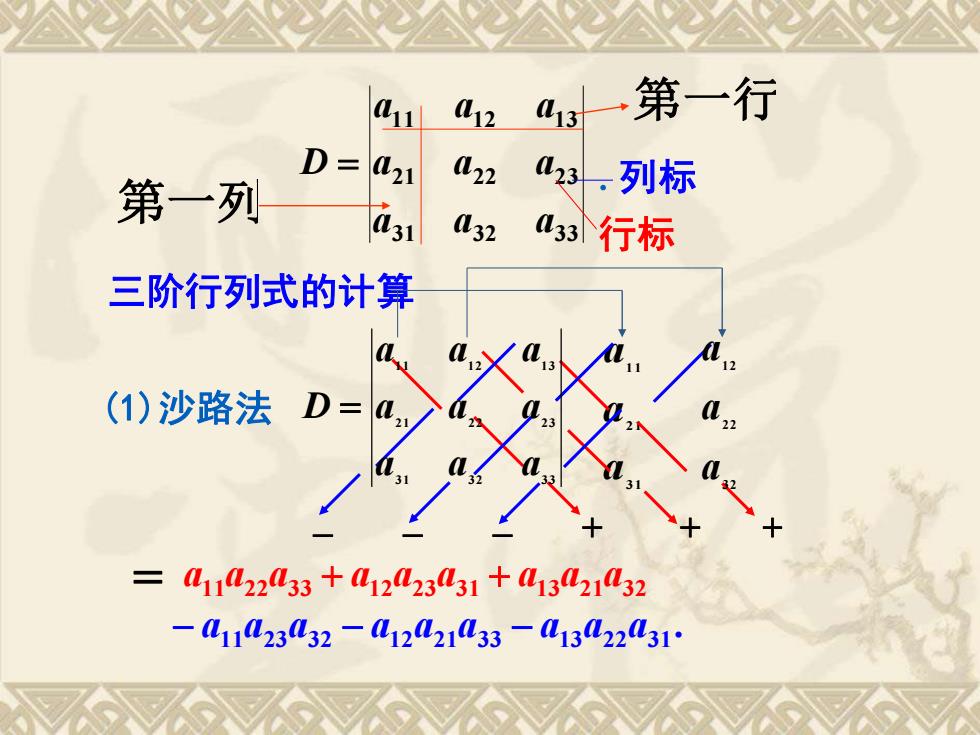
11 L12 13 第一行 D=a21 L22 第一列 23.列标 a31 32 3行标 三阶行列式的计算 (1)沙路法D =41142233+41223431+41342132 -4112332-01221L33-L132231
31 21 11 a a a − − − + + + . − a11a23a32 − a12a21a33 − a13a22a31 (1)沙路法 三阶行列式的计算 = a11a22a33 + a12a23a31 + a13a21a32 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = .列标 行标 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 a a a a a a a a a D = 32 22 12 a a a 第一行 第一列
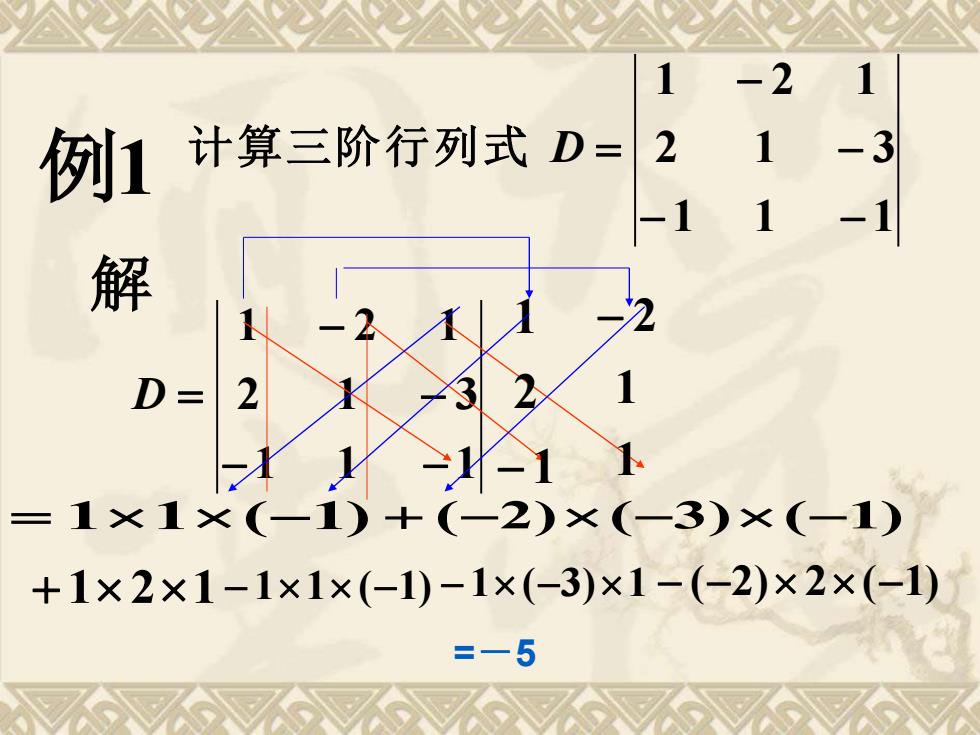
例1 计算三阶行列式D= 2 解 D :1×1×(-1)+(一2)×(-3)×(一1) +1×2×1-1×1×(-1)-1×(-3)×1-(-2)×2×(-1) =5
例1 1 1 1 2 1 3 1 2 1 − − − − 计算三阶行列式 D = 解 1 1 1 2 1 3 1 2 1 − − − − D = = 11(−1) + (−2)(−3)(−1) =-5 1 2 1 − 1 1 − 2 + 1 21 − 11(−1) − 1(−3)1 − (−2) 2(−1)
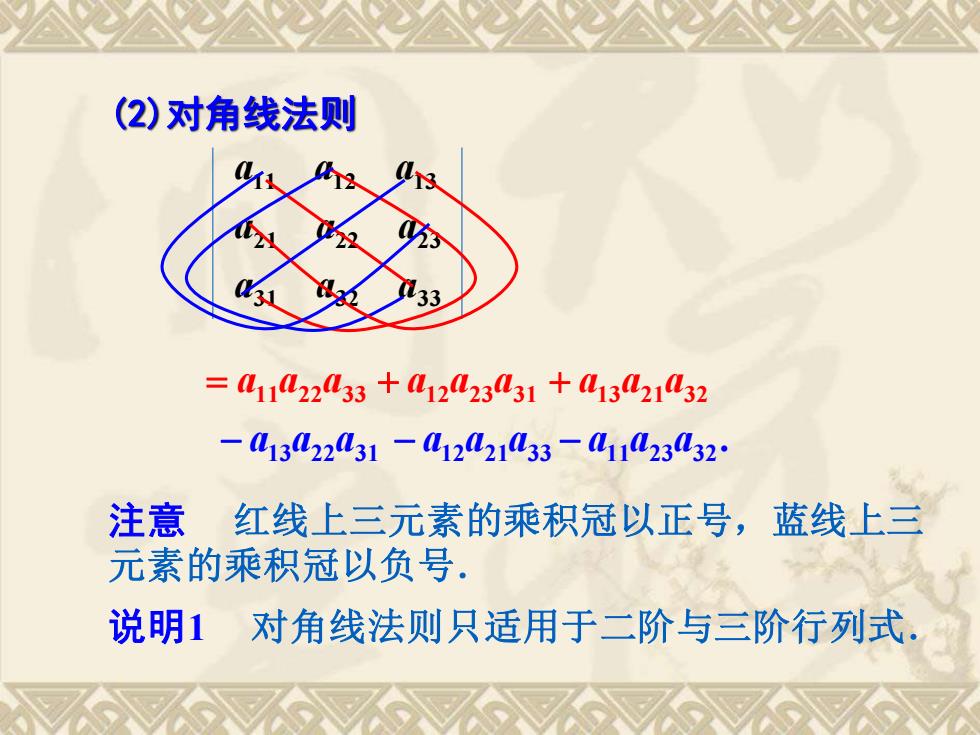
(2)对角线法则 =41142233+412423031+0132132 -41322L31-L12021L33一112332 注意 红线上三元素的乘积冠以正号,蓝线上三 元素的乘积冠以负号. 说明1 对角线法则只适用于二阶与三阶行列式
31 32 33 21 22 23 11 12 13 a a a a a a a a a = a11a22a33 . 11 23 32 − a a a (2)对角线法则 注意 红线上三元素的乘积冠以正号,蓝线上三 元素的乘积冠以负号. 说明1 对角线法则只适用于二阶与三阶行列式. + a12a23a31 + a13a21a32 13 22 31 − a a a 12 21 33 − a a a

2.三阶行列式包括3!项,每一项都是位于不同行, 不同列的三个元素的乘积,其中三项为正,三项为 负 -2 例2 D 2 1 -3 -1 1 -1 解 -31x1×(-1)+(-2)×(-3)×(-1) 1 +×2x11xx((2)×2×(-1)-1×(-3)×1=-5
2.三阶行列式包括3!项,每一项都是位于不同行, 不同列的三个元素的乘积,其中三项为正,三项为 负. 例2 1 1 1 2 1 3 1 2 1 − − − − D = 1 1 1 2 1 3 1 2 1 − − − − D = 解 = 11(−1) + (− 2)(− 3)(−1) + 121−11(−1)− (− 2)2(−1) −1(− 3)1= −5

例3计算三阶行列式D 解 按对角线法则,有 D=1×2×(-2)+2×1×(-3)+(-4)×(-2)×4 -1×1×4-2×(-2)×(-2)-(-4)×2×(-3) =-4-6+32-4-8-24 =-14
- 3 4 - 2 - 2 2 1 1 2 - 4 例3 计算三阶行列式 D = 解 按对角线法则,有 D =1 2(−2) + 21(−3) + (−4)(−2) 4 − 11 4 − 2(−2)(−2) − (−4) 2(−3) = −4 − 6 + 32 − 4 − 8 − 24 = −14