厦门大学：《量子化学 Quantum Chemistry》课程电子教案（教学课件）Chapter 3 矩阵与算符 Matrix and operator

矩阵和矩阵相乘 a11a12 C C12 a21 a22 b2 b22 … C=AB= C21 C22 C2k n…amb b之 Cn2 Cnk nxm m×k nxk

矩阵和矩阵相乘             =                         = = n n n k k k m m m k k k n n n m m m c c c c c c c c c b b b b b b b b b a a a a a a a a C AB             1 2 2 1 2 2 2 1 1 1 2 1 1 2 2 1 2 2 2 1 1 1 2 1 1 2 2 1 2 2 2 1 1 1 2 1 nm mk nk

Cu= (i=1,2,,n,jF1,2,,k) (3.17) av2 ym … C12 021 0422 C2m b21 b22 … bak C21 C22 C2k n2 Cn2

= = m p ij aip ppj c 1 (i = 1, 2, …, n, j= 1,2, …, k) (3.17)             =                         n n n k k k m m m k k k n n n m m m c c c c c c c c c b b b b b b b b b a a a a a a a a             1 2 2 1 2 2 2 1 1 1 2 1 1 2 2 1 2 2 2 1 1 1 2 1 1 2 2 1 2 2 2 1 1 1 2 1

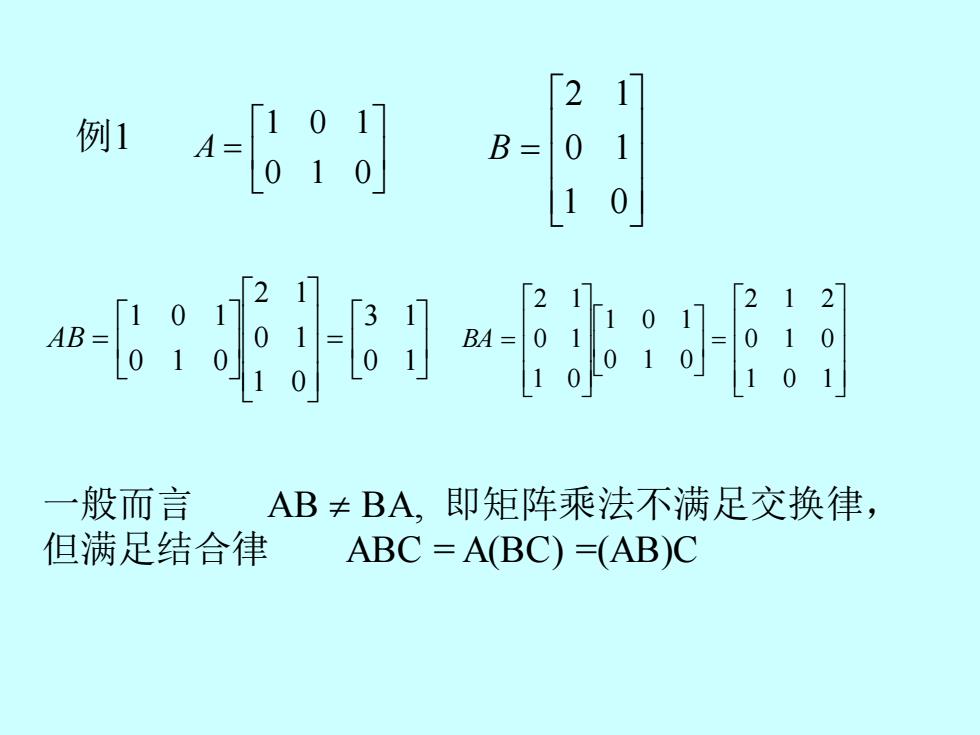
例1 21 B= 01 12 一 般而言 AB≠BA,即矩阵乘法不满足交换律， 但满足结合律 ABC=A(BC)=(AB)C

例1       = 0 1 0 1 0 1 A           = 1 0 0 1 2 1 B       =                 = 0 1 3 1 1 0 0 1 2 1 0 1 1 0 0 1 AB           =                = 1 0 1 0 1 0 2 1 2 0 1 1 0 0 1 1 0 0 1 2 1 BA 一般而言 AB  BA, 即矩阵乘法不满足交换律， 但满足结合律 ABC = A(BC) =(AB)C

转置矩阵、共轭矩阵、转置共轭矩阵 A=[agjlnxm AT=[ajil mxn A*=[aj*]nxm (3.18) 如4】-公 列4a 如果 F=ABC…X 则 FH=(ABC...X)H=XH...CHBHA (3.19)

转置矩阵、共轭矩阵、转置共轭矩阵 A = [aij] nm AT = [aji] mn A* = [aij*] nm 例2       = 2 1 2 i i A       = 2 2 1 i i A T       − − = 2 1 2 i i A*       − − = 2 2 1 i i A H (3.18) 如果 F = ABCX 则 FH = (ABCX)H = XHCHBHA (3.19)