
13.2质点素的达朗贝尔原理 设质点象由n个质点组成,其中任一质点i的质 量为m,其如速度为把作用在此质点上的力分为 主动力的合力F、约束力的合力为F,对这个质点 上假想地加上它的惯性力Fi=m:,则由质点的达 朗贝尔原理,有 F+FN,+F=0(i=1,2,.,n) 即:质点系中每个质点上作用的主动力、约束力和 它的惯性力在形式上组成平衡力系。这就是质点系 的达朗贝尔原理
设质点系由 n 个质点组成, 其中任一质点i的质 量为mi , 其加速度为ai , 把作用在此质点上的力分为 主动力的合力Fi、约束力的合力为FNi,对这个质点 上假想地加上它的惯性力FIi=-miai , 则由质点的达 朗贝尔原理,有 N I 0 ( 1, 2, , ) i i i F F F + + = = i n 13.2 质点系的达朗贝尔原理 即:质点系中每个质点上作用的主动力、约束力和 它的惯性力在形式上组成平衡力系。这就是质点系 的达朗贝尔原理

13.2质点系的达朗贝尔原理 把作用在第个质点上的所有力分为外力的合力 为F,内力的合力为F0,则有 F°+F0+F,=0i=1,2,m) 质点系中第个质点上作用的外力、内力和它的惯性 力在形式上组成平衡力条。由静力学知,空间任意 力系平衡的充分必要条件是力条的主矢和对于任一 点的主矩等于零,即 ∑Fe+ΣF,0+∑F,=0 ΣMo(Fe)+ΣMo(F)+ΣM。(F)=0
把作用在第i个质点上的所有力分为外力的合力 为Fi (e) , 内力的合力为Fi (i) ,则有 (e) (i) I 0 ( 1, 2, , ) i i i F F F + + = = i n 13.2 质点系的达朗贝尔原理 质点系中第i个质点上作用的外力、内力和它的惯性 力在形式上组成平衡力系。由静力学知,空间任意 力系平衡的充分必要条件是力系的主矢和对于任一 点的主矩等于零,即 (e) (i) Σ Σ Σ I 0 F F F i i i + + = (i) (e) Σ I O O ( ) Σ ( ) i O Σ ( ) 0 M F M F M F i i + + =

13.2质点素的达朗贝尔原理 因为质点系的内力总是成对出现,且等值、反向、共 线,因此有2F0=0和∑Mo(F=0,于是的有 ΣFe+2F,=0 ΣM.(F)+ΣM,(E)=0 即:作用在质点条上的所有外力与虚如在每个质点 上的惯性力在形式上组成平衡力条。这是质点条达 朗贝尔原理的又一表述。 称F为惯性力系的主矢,∑Mo(F)为惯性力 象的主矩
因为质点系的内力总是成对出现, 且等值、反向、共 线, 因此有ΣFi (i)= 0和ΣMO(Fi (i)) = 0, 于是的有 即:作用在质点系上的所有外力与虚加在每个质点 上的惯性力在形式上组成平衡力系。这是质点系达 朗贝尔原理的又一表述。 13.2 质点系的达朗贝尔原理 (e) Σ Σ I i 0 F F + =i (e) Σ I O i O ( ) Σ ( ) 0 M F M F + = i 称ΣFIi为惯性力系的主矢, ΣMO(FIi )为惯性力 系的主矩
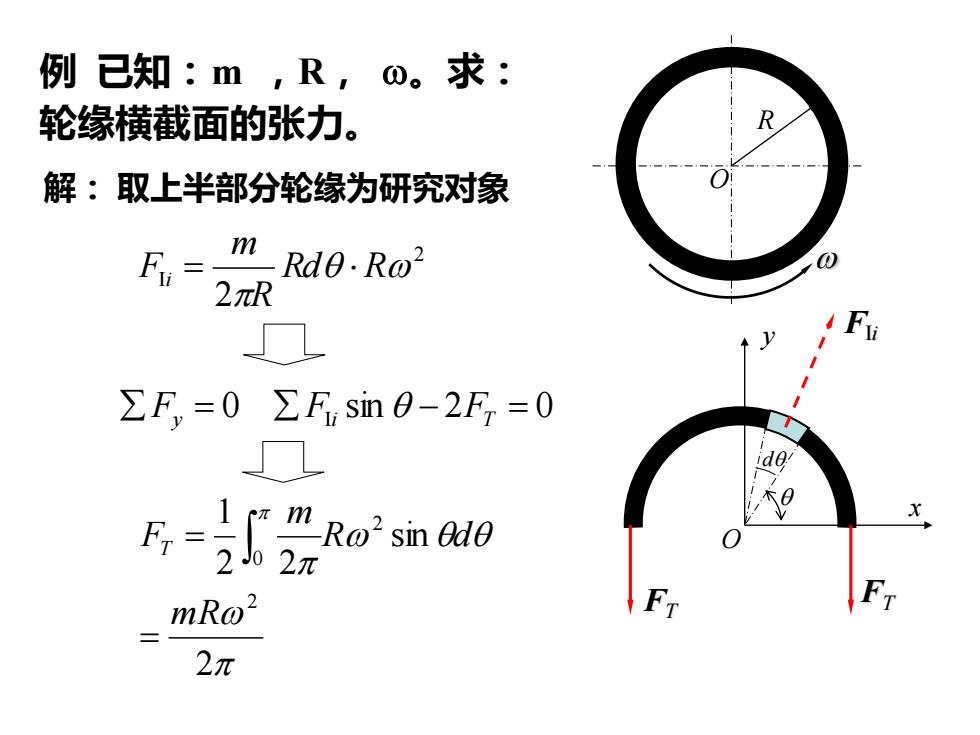
例已知:m,R,Q。求: 轮缘横截面的张力。 解:取上半部分轮缘为研究对象 Rd0.Ro 2πR ΣF,=0∑F,sin0-2F=0 片2 Rni'sin X mRo2 2π
O x y FIi d F FT T w O R 例 已知:m ,R, w。求: 轮缘横截面的张力。 解: 取上半部分轮缘为研究对象 2 2 w Rd R R m Fi = = 0 sin − 2 = 0 Fy Fi FT w w 2 sin 2 2 1 2 2 0 mR R d m FT = =

13.3刚体愤性力素的简化 用质点系的达朗贝尔原理求解质点系的动力学问 题,需要对质点内每个质点加上各自的惯性力,这些 惯性力也形成一个力系,称为惯性力条。下面用静力 学力系简化理论,求出惯性力条的主矢和主矩。 以FR表示惯性力条的主矢。由质心运动定理及质 点条的达朗贝尔原理 ΣFo+ΣF=0 得 F=ΣF=-∑Fe=-maC 此式表明:无论刚体作什么运动,惯性力系的主矢都等 于刚体的质量与其质心如速度的乘积,方向与质心如速 度的方向相反
用质点系的达朗贝尔原理求解质点系的动力学问 题,需要对质点内每个质点加上各自的惯性力,这些 惯性力也形成一个力系,称为惯性力系。下面用静力 学力系简化理论,求出惯性力系的主矢和主矩。 以FIR表示惯性力系的主矢。由质心运动定理及质 点系的达朗贝尔原理 13.3 刚体惯性力系的简化 (e) Σ Σ I 0 F F i i + = 得 (e) F F F a I I R i i C = = − = − Σ Σ m 此式表明:无论刚体作什么运动, 惯性力系的主矢都等 于刚体的质量与其质心加速度的乘积, 方向与质心加速 度的方向相反