
第十二章 动能定理 ·力的功 ·质点和质点系的动能 ·动能定理 ·善遍定理的综合应用举创 。功率·功率方程·机械效率
第十二章 动能定理 • 力的功 • 质点和质点系的动能 • 动能定理 • 普遍定理的综合应用举例 • 功率·功率方程·机械效率

引言 前两章是以动量和冲量为基础,建立了质点或质 点条运动量的变化与外力及外力作用时问之问的关系。 本章以功和动能为基础,建立质点或质点系动能的改 变和力的功之间的关系,即动能定理。不同于动量定 理和动量矩定理,动能定理是从能量的角度来分析质 点和质点系的动力学问题,有时是更为方便和有效的。 同时,它还可以建立机械运动与其它形式运动之间的 联条。 在介绍动能定理之前,先介绍有关的物理量:功 与动能
前两章是以动量和冲量为基础,建立了质点或质 点系运动量的变化与外力及外力作用时间之间的关系。 本章以功和动能为基础,建立质点或质点系动能的改 变和力的功之间的关系,即动能定理。不同于动量定 理和动量矩定理,动能定理是从能量的角度来分析质 点和质点系的动力学问题,有时是更为方便和有效的。 同时,它还可以建立机械运动与其它形式运动之间的 联系。 在介绍动能定理之前,先介绍有关的物理量:功 与动能。 引言

12.1力的功 12.1.1常力的功 设物体在常力F作用下沿直线走过路程5,如图, 则力所作的功W定义为 W-Fcos0.s=F.s 功是代数量。宅表示力在一段路程上的累积作用效应, 因此功为累积量。在国际单位制中,功的单位为:J (焦耳),1J=1Nm
12.1.1 常力的功 设物体在常力F作用下沿直线走过路程s,如图, 则力所作的功W定义为 W F s = = cos F s 功是代数量。它表示力在一段路程上的累积作用效应, 因此功为累积量。在国际单位制中,功的单位为:J (焦耳), 1J=1 N·m。 12.1力的功
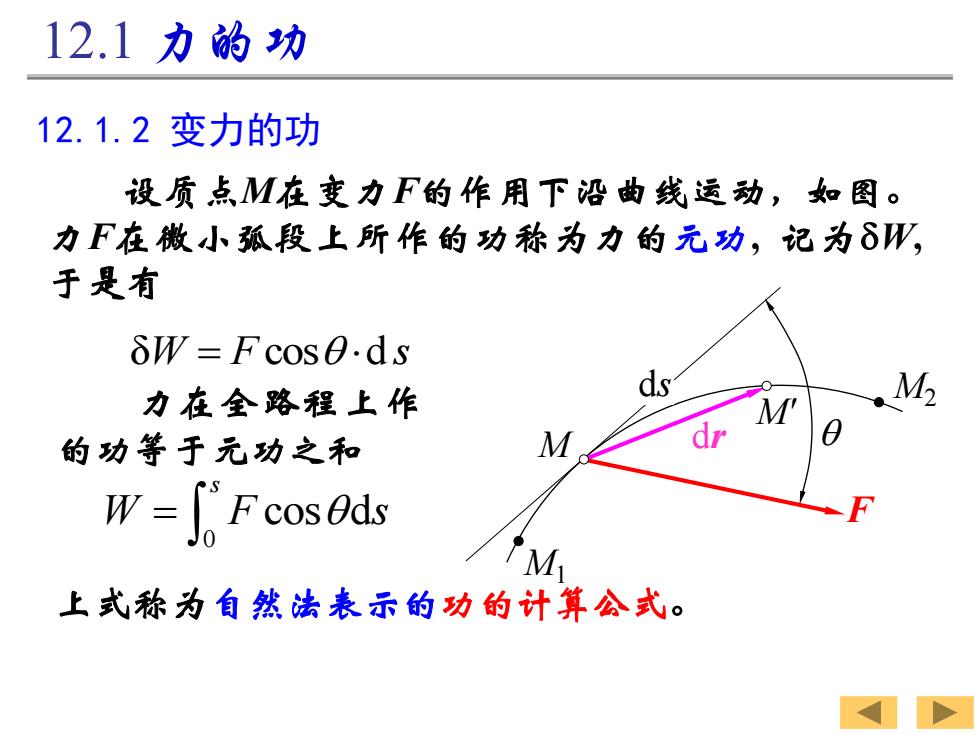
12.1力的功 12.1.2变力的功 设质点M在变力F的作用下沿曲线运动,如图。 力F在微小孤段上所作的功称为力的元功,记为δW, 于是有 δW=Fcosθ.ds 力在全路程上作 M2 的功等于元功之和 M W=[Fcosds 上式称为自然法表示的功的计算会式
12.1.2 变力的功 设质点M在变力F的作用下沿曲线运动,如图。 力F在微小弧段上所作的功称为力的元功, 记为dW, 于是有 δW F s = cos d 12.1 力的功 M' M1 M2 ds M dr F 力在全路程上作 的功等于元功之和 0 cos d s W F s = 上式称为自然法表示的功的计算公式

12.1力的功 上两式可写成关量点乘积形式 =∫下d 称为矢径法表示的功的计算公式。 在直角坐标系中 F=Fi+Fj+k,dr=dxi+dyj+dzk δW=Fdx+Fdy+Fdz W-(Fdx+F,dy+Fd=) 上式称为直角坐标法表示的功的计算公式,也称为功 的解析表达式
δW = F rd 2 1 d M M W = F r 称为矢径法表示的功的计算公式。 在直角坐标系中 d d d d F i j k, r i j k = + + = + + F F F x y z x y z δ d d d W F x F y F z = + + x y z 2 1 ( d d d ) M x y z M W F x F y F z = + + 12.1 力的功 上两式可写成矢量点乘积形式 上式称为直角坐标法表示的功的计算公式,也称为功 的解析表达式