
第7章 点的合成运动 7.1相对运动·牵连运动·绝对运动 7.2点的速度合成定理 7.3点的如速度合成定理
第 7 章 点的合成运动 7.1 相对运动·牵连运动·绝对运动 7.2 点的速度合成定理 7.3 点的加速度合成定理

7.1相对运动牵连运动绝对运动 通过观察可以发现,物体对一参考体的运动可以由几个运动 组合而成。例如,在上述的例子中,车轮上的点M是沿旋轮线运 动,但是知果以车厢作为参考体,则点M对于车厢的运动是简单 的圆周运动,车厢对于地面的运动是简单的平动。这样,轮缘上 一点的运动就可以看成为两个简单运动的合成,即点M相对于车 厢作圆周运动,同时车厢对地面作平动。于是,相对于某一参考 体的运动可由相对于其它参考体的几个运动组合而成,称这种运 动为合成运动
x y' x' y o' o M v 7.1 相对运动·牵连运动·绝对运动 通过观察可以发现,物体对一参考体的运动可以由几个运动 组合而成。例如,在上述的例子中,车轮上的点M是沿旋轮线运 动,但是如果以车厢作为参考体,则点M对于车厢的运动是简单 的圆周运动,车厢对于地面的运动是简单的平动。这样,轮缘上 一点的运动就可以看成为两个简单运动的合成,即点M相对于车 厢作圆周运动,同时车厢对地面作平动。于是,相对于某一参考 体的运动可由相对于其它参考体的几个运动组合而成,称这种运 动为合成运动

7.1相对运动牵连运动绝对运动 习惯上把固定在地球上的坐标系称为定参考系, 以0心y坐标系表示;固定在其它相对于地球运动的参考 体上的坐标象称为动参考系,以0xy'坐标条表示。 用点的合成运动理论分析点的运动时,必须选定两 个参考条,区分三种运动: ()动点相对于定参考条的运动,称为绝对运动; (2)动点相对于动参考条的运动,称为相对运动; (③)动参考条相对于定参考条的运动,称为牵连运动
习惯上把固定在地球上的坐标系称为定参考系, 以oxy坐标系表示;固定在其它相对于地球运动的参考 体上的坐标系称为动参考系,以o'x'y'坐标系表示。 7.1 相对运动·牵连运动·绝对运动 用点的合成运动理论分析点的运动时,必须选定两 个参考系,区分三种运动: (1) 动点相对于定参考系的运动,称为绝对运动; (2) 动点相对于动参考系的运动,称为相对运动; (3) 动参考系相对于定参考系的运动,称为牵连运动
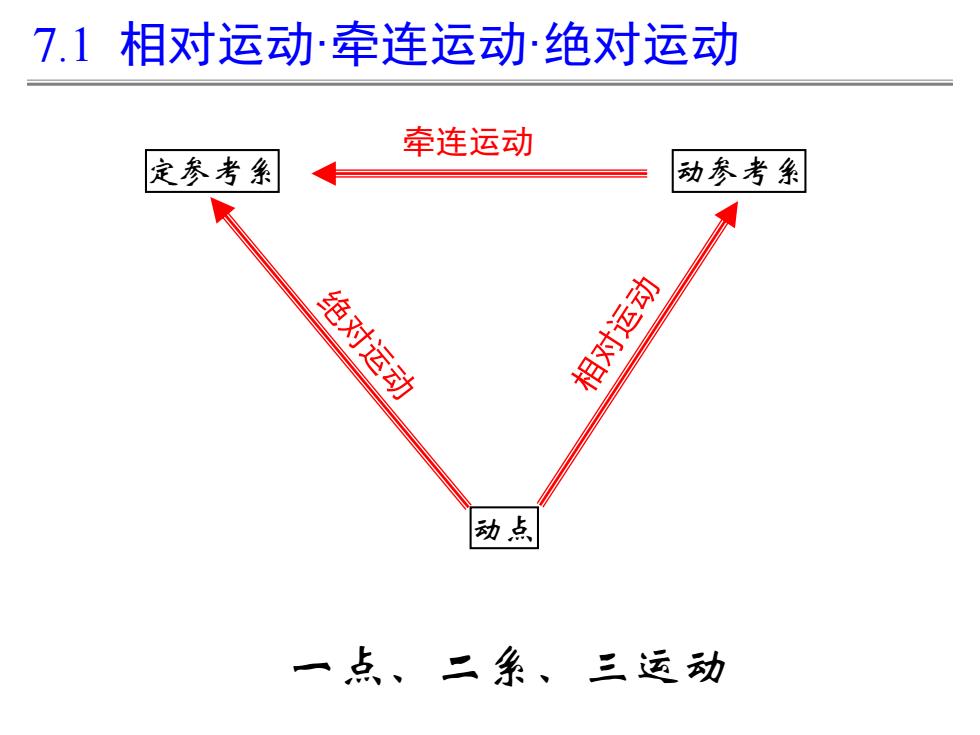
7.1相对运动牵连运动绝对运动 牵连运动 定参考系 动参考条 绝对运动 相对运动 动点 一点、二系、三运动
定参考系 动参考系 动点 牵连运动 一点、二系、三运动 7.1 相对运动·牵连运动·绝对运动

7.1相对运动牵连运动绝对运动 (1)动点相对于定参考系的速度、加速度和轨迹, 称为动点的绝对速度ya、绝对加速度1和绝对轨迹。 (2)动点相对于动参考条的速度、如速度和轨迹, 称为动点的相对速度y,、相对加速度·,和相对轨迹。 由于动参考条的运动是则体的运动而不是一个点 的运动,所以除非动参考条作平移,否则其上各点的 运动都不完全相同。因为动参考条与动点直接相关的 是动参考系上与动点相重合的那一点(牵连点),因此 定义: 在动参考系上与动点相重合的那一点(牵连点)的 速度和加速度称为动点的率连速度(用v表示)和牵连 如速度(用ae表示)
(1) 动点相对于定参考系的速度、加速度和轨迹, 称为动点的绝对速度va、绝对加速度aa和绝对轨迹。 (2) 动点相对于动参考系的速度、加速度和轨迹, 称为动点的相对速度vr、相对加速度ar和相对轨迹。 7.1 相对运动·牵连运动·绝对运动 由于动参考系的运动是刚体的运动而不是一个点 的运动,所以除非动参考系作平移,否则其上各点的 运动都不完全相同。因为动参考系与动点直接相关的 是动参考系上与动点相重合的那一点(牵连点),因此 定义: 在动参考系上与动点相重合的那一点(牵连点)的 速度和加速度称为动点的牵连速度(用ve表示)和牵连 加速度(用ae表示)