
第十六章虚位移康理 条统的约束及其分类 口虚位移及其计算
第十六章 虚位移原理 • 系统的约束及其分类 • 虚位移及其计算

引 言 虚位移原理,是用分析的方法来研究任意 质点系的平衡问题。这部分内容称为分析静力 学。虚位移原理给出的平衡条件,对于任意质 点系的平衡都是必要与充分的,因此它是解决 质点系平衡问题的普遍原理。同时,将虚位移 原理和达朗伯原理相结合,可以导出动力学普 遍方程和拉格朗日方程,从而得到求解质点系 动力学问题的又一个普遍的方法
引 言 虚位移原理,是用分析的方法来研究任意 质点系的平衡问题。这部分内容称为分析静力 学。虚位移原理给出的平衡条件,对于任意质 点系的平衡都是必要与充分的,因此它是解决 质点系平衡问题的普遍原理。同时,将虚位移 原理和达朗伯原理相结合,可以导出动力学普 遍方程和拉格朗日方程,从而得到求解质点系 动力学问题的又一个普遍的方法

约束类型及分类 限制质点系中各质点的位置和运动的条件称为约束。表 示这些限制条件的表达式称为约束方程。根据约束形式及其 性质,约束可分以下类型: 一、几何约束与运动约束 限制质点或质点系在空间的几何位置的约束称为几何约束。 如: X M(x,y)x2+y2=12
限制质点系中各质点的位置和运动的条件称为约束。表 示这些限制条件的表达式称为约束方程。根据约束形式及其 性质,约束可分以下类型: 一、几何约束与运动约束 限制质点或质点系在空间的几何位置的约束称为几何约束。 如: O x y M (x, y) l 2 2 2 x + y = l 约束类型及分类
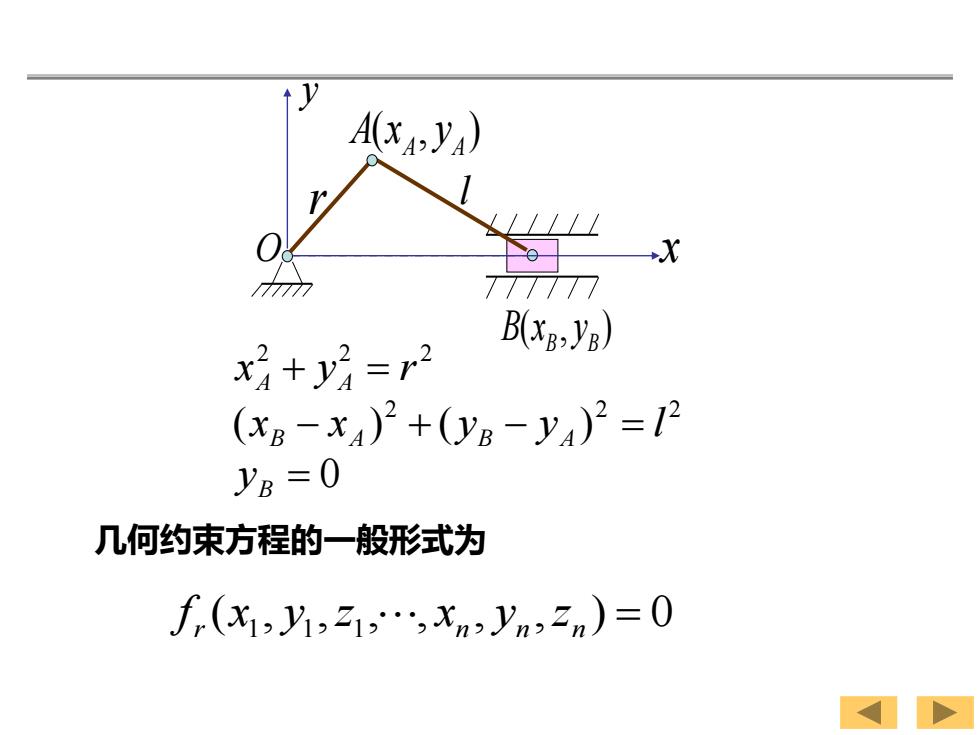
A(YA) X T1777 x+y房=2 B(Xg:Yg) (XB-x)+(Ya-y4)2=12 YB=0 几何约束方程的一般形式为 f(x1,乃,21,.,xn,yn,2n)=0
O ( , ) A A A x y ( , ) B B B x y r l x y 0 ( ) ( ) 2 2 2 2 2 2 = − + − = + = B B A B A A A y x x y y l x y r 几何约束方程的一般形式为 f r (x1 , y1 ,z1 , , xn , yn ,zn ) = 0

不仅能限制质点系的位置,而目能限制质点系中各质点的 速度的约束称为运动约束。 ↑y 为几何约束方程。 无法显示该图片 yB=r B() X xg一r0=0为运动约束方程。 运动约束方程的一般形式为 f(x1,y,1,Xn,yn,2n,元,y1,1,.,元n,少n,车n)=0
不仅能限制质点系的位置,而且能限制质点系中各质点的 速度的约束称为运动约束。 ( , ) B B B x y B v O x y C r y r 为几何约束方程。 B = x B −r = 0 为运动约束方程。 运动约束方程的一般形式为 f r (x1 , y1 ,z1 , , xn , yn ,zn , x 1 , y 1 ,z 1 , , x n , y n ,z n ) = 0