
电动力学 Classical Electrodynamics 数学准备 2014年8月 石河子大学理学院物理系 郭志 荣编写 1
2014年8月 石河子大学理学院物理系 郭志 荣 编写 电动力学 Classical Electrodynamics 数学准备 1

矢量分析 ·矢量(函数) a=a(t)=a,(t)i+a,(t)j+a.(t)k; a=/a;+a;+a2 也可用矩阵形式书写 2 ax a=a,a,a.)ora= a ay a ·矢量(函数)求和 0 a±b=[a,±b5+[4,±b,]+[a.±b]k =(a±bx,a,±b,a.±b 2014年8月 石河子大学理学院物理系 郭志 荣编写 2
2014年8月 石河子大学理学院物理系 郭志 荣 编写 矢量分析 • 矢量(函数) – 也可用矩阵形式书写 • 矢量(函数)求和 ( ) ( ) ( ) ( ) 2 2 2 ; x y z a ax ay az a = a t = a t i + a t j + a t k = + + ( ) = = z y x x y z a a a a a a a or a , , ( ) x x y y z z x x y y z z a b a b a b a b a b i a b j a b k = = + + , , x a az a y a 2

矢量分析 ·点乘ab=(a,a,ab =lacoso b =ab,+a b +a.b a×b 大小ab sin 方向右手旋螺 ·差乘 b axb=a, ay a. a =(a,b.-a.b,+(a.b,-ab.)j+(ab,-a,b axb=-bxa 2014年8月 石河子大学理学院物理系 郭志 荣编写 3
2014年8月 石河子大学理学院物理系 郭志 荣 编写 矢量分析 • 点乘 • 差乘 ( ) x x y y z z z y x x y z a b a b a b a b b b b a b a a a = + + = = , , cos (a b a b )i (a b a b )j (a b a b )k b b b a a a i j k a b y z z y z x x z x y y x x y z x y z = − + − + − = a b b a = − a b 方向右手旋螺 大小a b sin a b 3

矢量分析 。混合积c-(a×) -大小Nd,axbsin 0 -等于ā,为邻边的平行六面体的面积 -底面积a×b=absin中 -高dcos0=ccos0 -体积a.5威)万.×a 一混合积的性质: a a-6xc)=万.(exa)=c-a×b) =-a.(cxB)=-B.(axc)=-c.(Bxa) 2014年8月 石河子大学理学院物理系 郭志 荣编写 4
2014年8月 石河子大学理学院物理系 郭志 荣 编写 矢量分析 • 混合积 – 大小 – 等于 为邻边的平行六面体的面积 – 底面积 – 高 – 体积 或 – 混合积的性质: c (a b) c a b sin a b = absin c cos = ccos a b c , , a b c a (b c) b (c a) ( ) ( ) ( ) a (c b) b (a c) c (b a) a b c b c a c a b = − = − = − = = 4
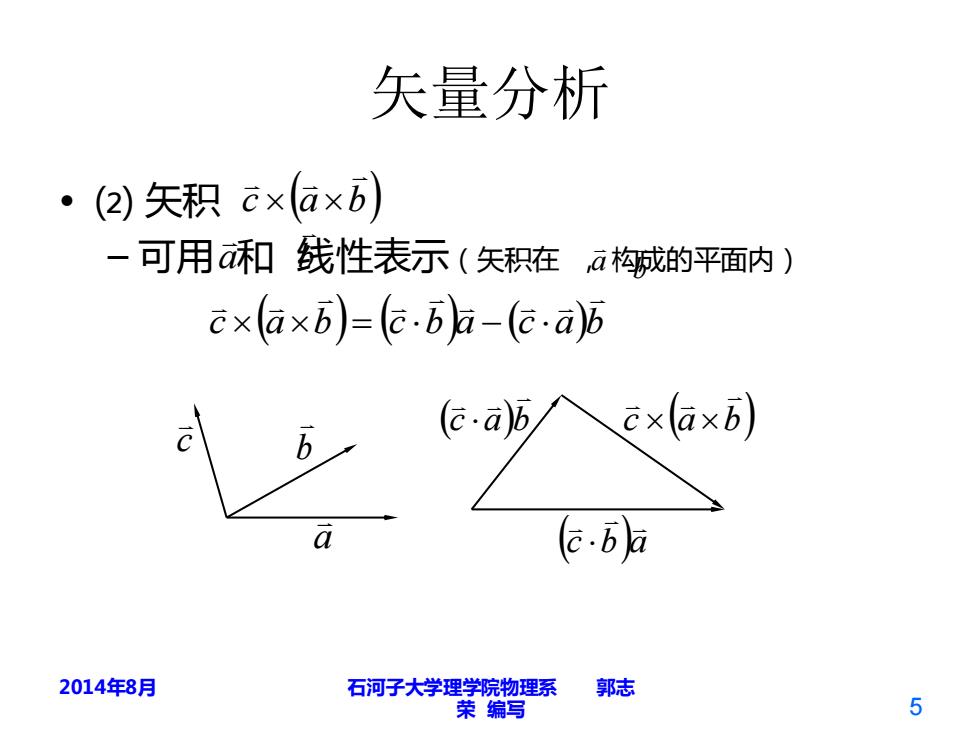
矢量分析 ·(2)矢积c×(axb) -可用和残性表示(矢积在,ā构成的平面内) cxaxB)=(e.b后-(aa)b b e-ad人cxax6 a (.a 2014年8月 石河子大学理学院物理系 郭志 荣编写 5
2014年8月 石河子大学理学院物理系 郭志 荣 编写 矢量分析 • ⑵ 矢积 – 可用 和 线性表示(矢积在 , 构成的平面内) c (a b) a b b a c (a b) (c b)a (c a)b = − a b c (c a)b (c b)a c (a b) 5