
§64相对论理论的四维形式 1
1 §6.4 相对论理论的四维形式

在相对论中时间和空间不可分割, 当参考系改变时,时空坐标互相 变换,三维空间和一维时间构成 一个统一体 四维时空。 2
2 在相对论中时间和空间不可分割, 当参考系改变时,时空坐标互相 变换,三维空间和一维时间构成 一个统一体 ——四维时空

四维时空理论可用简洁的四 维形式表述出来。利用这种形式可以很 清楚地显示出一些物理量之间的内在联 系,并且可以把相对性原理用非常明显 的形式表达出来。 3
3 四维时空理论可用简洁的四 维形式表述出来。利用这种形式可以很 清楚地显示出一些物理量之间的内在联 系,并且可以把相对性原理用非常明显 的形式表达出来
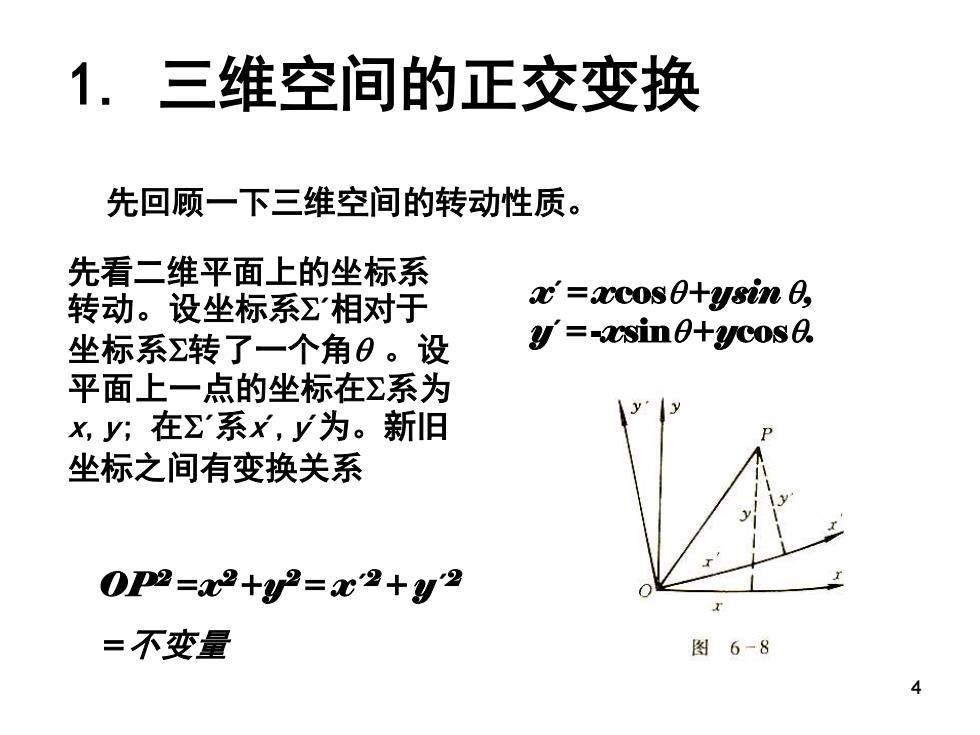
1.三维空间的正交变换 先回顾一下三维空间的转动性质。 先看二维平面上的坐标系 转动。设坐标系Σ相对于 x=xcos0+ysin 0, 坐标系转了一个角0。设 =sin0+ycos0 平面上一点的坐标在Σ系为 x,y,在∑系x,y为。新旧 坐标之间有变换关系 0P2=2+2=x2+U2 =不变量 图6-8 4
4 先回顾一下三维空间的转动性质。 先看二维平面上的坐标系 转动。设坐标系´相对于 坐标系转了一个角 。设 平面上一点的坐标在系为 x,y; 在´系x´ ,y´为。新旧 坐标之间有变换关系 x´=xcos+ysin , y´=-xsin+ycos. OP2=x2+y2= x´ 2+ y´ 2 =不变量 1. 三维空间的正交变换

正交变换 0P2=2+2=x2+/2=不变量 满足此式的二维平面上的线性变换称为 正交变换。坐标系转动属于正交变换。 5
5 满足此式的二维平面上的线性变换称为 正交变换。坐标系转动属于正交变换。 OP2=x2+y2= x´ 2+ y´ 2=不变量 正交变换