
第十三章: 达朗贝尔原理 达朗贝尔原理 则体惯性力系的简化
第十三章 达朗贝尔原理 • 达朗贝尔原理 • 刚体惯性力系的简化

引言 前面介绍的动力学善遍定理,为解决质点 象动力学问题提供了一种普遍的方法。达朗 贝尔原理为解决非自由质点系动力学问题提 供了另一种普遍的方法。这种方法的特点是: 用静力学研究平衡问题的方法来研究动力学 的不平衡问题,因此这种方法又叫动静法。由 于静力学研究平衡问题的方法比较简单,也容 易幸握,因此动静法在工程中被广泛使用
前面介绍的动力学普遍定理, 为解决质点 系动力学问题提供了一种普遍的方法。达朗 贝尔原理为解决非自由质点系动力学问题提 供了另一种普遍的方法。这种方法的特点是: 用静力学研究平衡问题的方法来研究动力学 的不平衡问题, 因此这种方法又叫动静法。由 于静力学研究平衡问题的方法比较简单, 也容 易掌握, 因此动静法在工程中被广泛使用。 引言
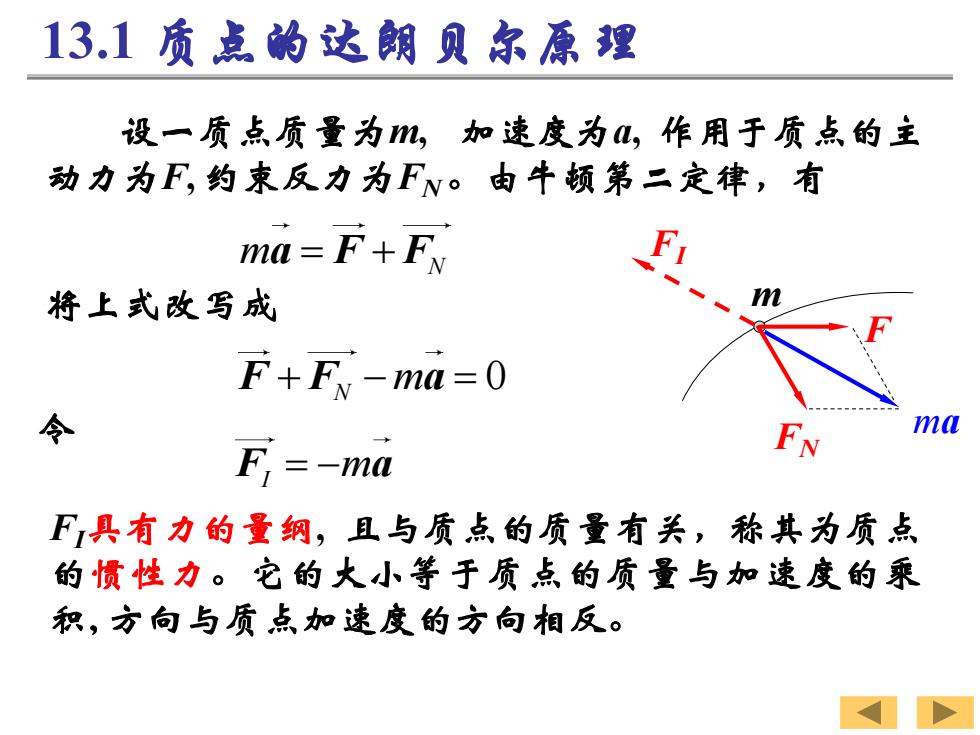
13.1质点的达朗贝尔原理 设一质点质量为m,加速度为4,作用于质点的主 动力为F,约束反力为FN。由牛顿第二定律,有 ma=F+Ex 将上式改写成 F+Fy-ma=0 令 F=-ma F具有力的量纲,且与质点的质量有关,称其为质点 的惯性力。它的火小等于质点的质量与加速度的乘 积,方向与质点如速度的方向相反
设一质点质量为m, 加速度为a, 作用于质点的主 动力为F, 约束反力为FN。由牛顿第二定律,有 将上式改写成 令 F a I = −m 13.1 质点的达朗贝尔原理 m = + N a F F 0 F F a + − = N m FI具有力的量纲, 且与质点的质量有关,称其为质点 的惯性力。它的大小等于质点的质量与加速度的乘 积, 方向与质点加速度的方向相反。 m F FN FI ma

13.1质点的达朗贝尔原理 则有 F+FN+F=0 即:在质点运动的任一瞬时,作用于质点上的主动力、 约束反力和假想如在质点上的惯性力构成形式上的平 衡力系。这就是质点的达朗贝尔原理。 应该强调指出,质点并非处于平衡状态,这样 做的目的是将动力学问题转化为静力学问题求解。 达朗贝尔原理与虚位移原理构成了分析力学的基础
即:在质点运动的任一瞬时, 作用于质点上的主动力、 约束反力和假想加在质点上的惯性力构成形式上的平 衡力系。这就是质点的达朗贝尔原理。 则有 0 F F F + + = N I 应该强调指出,质点并非处于平衡状态,这样 做的目的是将动力学问题转化为静力学问题求解。 达朗贝尔原理与虚位移原理构成了分析力学的基础。 13.1 质点的达朗贝尔原理

例1球磨机的滚筒以匀角速度0绕水平轴O转动,内装钢球和需要粉碎的 物料,钢球被筒壁带到一定高度脱离筒壁,然后沿抛物线轨迹自由落下,从而 击碎物料,如图。设滚筒内壁半径为r,试求钢球的脱离角。 解:以某一尚未脱离筒壁的钢球为研究对像,受力如图。钢球未脱离筒 壁前,作圆周运动,其加速度为 a,=0 a=ro2 惯性力F的大小为F=mro2 假想地加上惯性力,由达朗贝尔原理 ∑Fn=0:F+mg cos-F=0 F@2 Fv =mg(-cose) 8 这就是钢球在任一位置日时所受的法向反力,显然当钢球脱离筒壁 时,Fv=0,由此可求出其脱离角a为 a arccos
例1 球磨机的滚筒以匀角速度w 绕水平轴O转动, 内装钢球和需要粉碎的 物料, 钢球被筒壁带到一定高度脱离筒壁, 然后沿抛物线轨迹自由落下, 从而 击碎物料, 如图。设滚筒内壁半径为r,试求钢球的脱离角a。 解:以某一尚未脱离筒壁的钢球为研究对象, 受力如图。钢球未脱离筒 壁前, 作圆周运动,其加速度为 = 0 a 2 an = rw 惯性力FI的大小为 假想地加上惯性力,由达朗贝尔原理 0: cos 0 = + − = F F mg F n N I O M r w a F FN mg FI 2 F mr I = w ( cos ) 2 w = − g r FN mg 这就是钢球在任一位置 时所受的法向反力, 显然当钢球脱离筒壁 时, FN=0 , 由此可求出其脱离角a为 arccos( ) 2 g rw a =