
6.3 相对论的时空理论 1
1 6.3 相对论的时空理论

1.相对论时空结构 上一节中引入了两事件的间隔的概念。为了 简单,以第一事件为时空原点(0,0,0,0), 设第二事件时空坐标为,3,)。这两事件 的间隔定义为 s2=c2t2-x2-y2-z2=c2t2-r2 r=√x2+y2+z2为两事件的空间距离 2
2 上一节中引入了两事件的间隔的概念。为了 简单,以第一事件为时空原点(0,0,0,0), 设第二事件时空坐标为(x,y,z,t) 。这两事件 的间隔定义为 2 2 2 2 2 2 2 2 2 s = c t − x − y − z = c t − r r = x 2 + y 2 + z 2 为两事件的空间距离 1. 相对论时空结构

两事件的间隔可以取任何数值,区分三种情况 Q)g2=0, 2)82>0, (3)82<0,即 即r=ct。两 即r<ct。两 r>ct。两事件的 事件可以用 事件通过低于 空间距离超过光 光波相联系。 光速的作用联 波在时间所能传 系。 播的距离。 从一个惯性系到另一个惯性系 的变换中,间隔2保持不变。 上述三种间隔的划分是绝对的。 不因参考系变换而改变。 3
3 两事件的间隔可以取任何数值,区分三种情况 (1) s 2=0 , 即r=ct。两 事件可以用 光波相联系。 (2) s 2>0, 即 r<ct。两 事件通过低于 光速的作用联 系。 (3) s 2<0,即 r>ct。两事件的 空间距离超过光 波在时间t所能传 播的距离。 从一个惯性系到另一个惯性系 的变换中,间隔s 2保持不变。 上述三种间隔的划分是绝对的。 不因参考系变换而改变
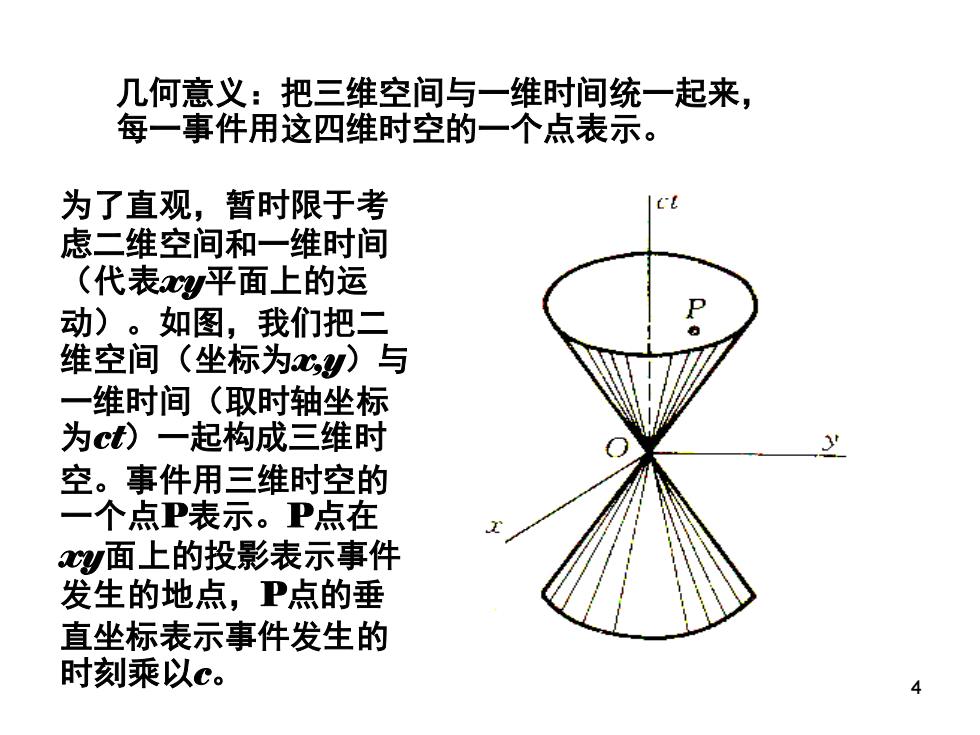
几何意义:把三维空间与一维时间统一起来, 每一事件用这四维时空的一个点表示。 为了直观,暂时限于考 虑二维空间和一维时间 (代表y平面上的运 动)。如图,我们把二 维空间(坐标为心)与 一维时间(取时轴坐标 为c)一起构成三维时 空。事件用三维时空的 一个点P表示。P点在 2以面上的投影表示事件 发生的地点,P点的垂 直坐标表示事件发生的 时刻乘以c
4 为了直观,暂时限于考 虑二维空间和一维时间 (代表xy平面上的运 动)。如图,我们把二 维空间(坐标为x,y)与 一维时间(取时轴坐标 为ct)一起构成三维时 空。事件用三维时空的 一个点P表示。P点在 xy面上的投影表示事件 发生的地点,P点的垂 直坐标表示事件发生的 时刻乘以c。 几何意义:把三维空间与一维时间统一起来, 每一事件用这四维时空的一个点表示
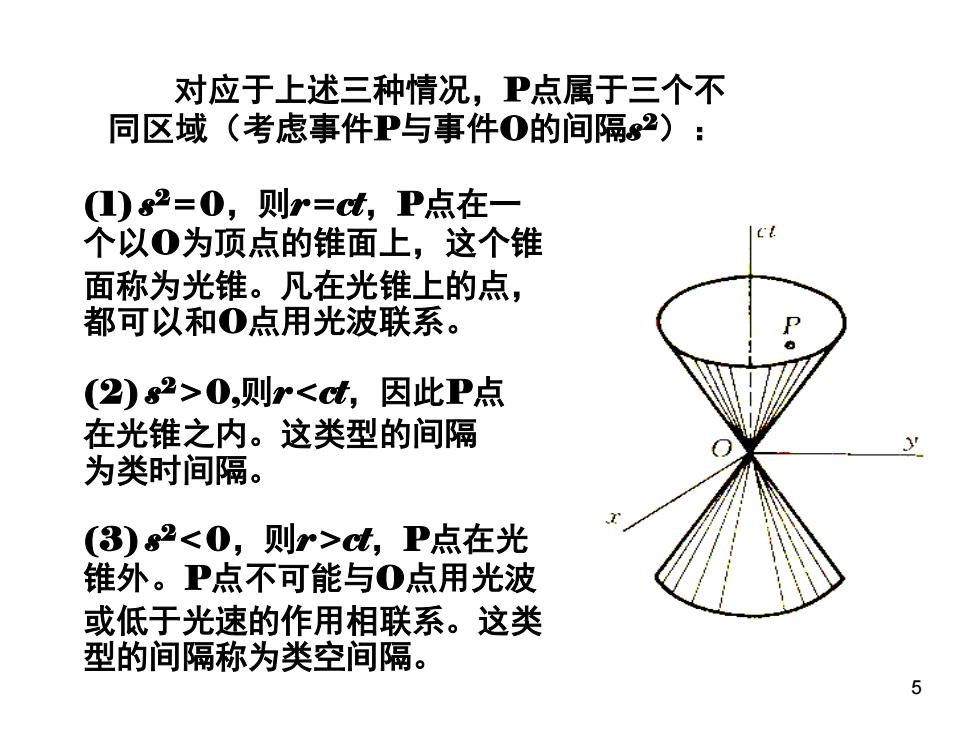
对应于上述三种情况,P点属于三个不 同区域(考虑事件P与事件0的间隔2): 1)2=0,则r=t,P点在一 个以0为顶点的锥面上,这个锥 面称为光锥。凡在光锥上的点, 都可以和0点用光波联系。 (2)2>0,则r<t,因此P点 在光锥之内。这类型的间隔 为类时间隔。 ()g2<0,则r>t,P点在光 锥外。P点不可能与0点用光波 或低于光速的作用相联系。这类 型的间隔称为类空间隔。 5
5 对应于上述三种情况,P点属于三个不 同区域(考虑事件P与事件O的间隔s 2): (1) s 2=0,则r=ct,P点在一 个以O为顶点的锥面上,这个锥 面称为光锥。凡在光锥上的点, 都可以和O点用光波联系。 (2) s 2>0,则r<ct,因此P点 在光锥之内。这类型的间隔 为类时间隔。 (3) s 2<0,则r>ct,P点在光 锥外。P点不可能与O点用光波 或低于光速的作用相联系。这类 型的间隔称为类空间隔