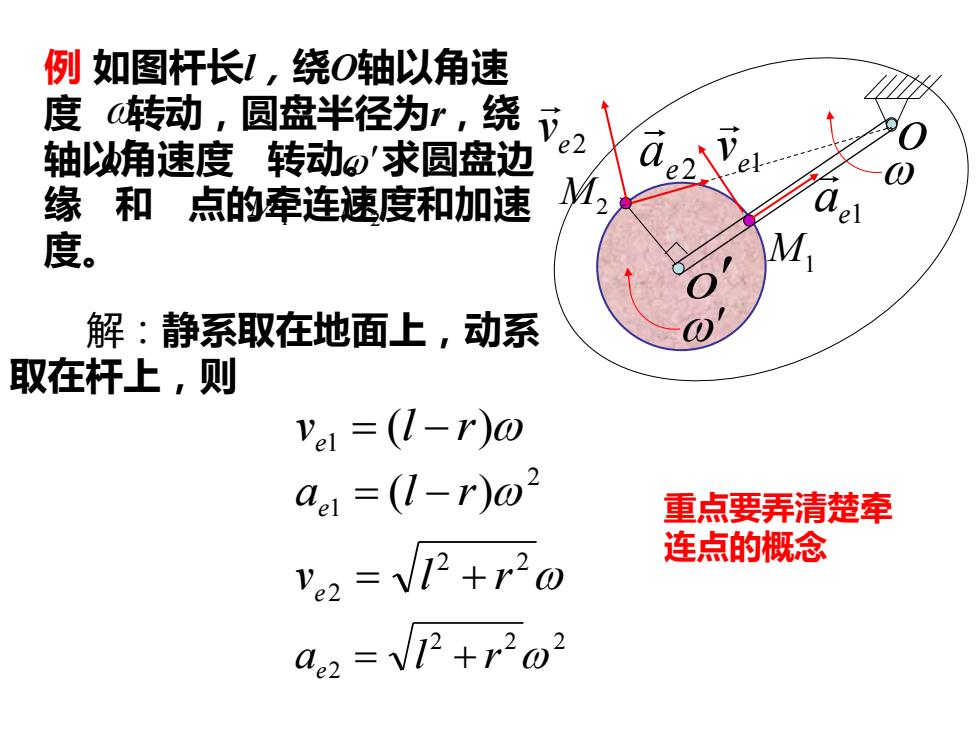
例如图杆长1,绕0轴以角速 度转动,圆盘半径为r,绕 轴角速度转动求圆盘边 e2 缘和点的牵连速度和加速 度。 解:静系取在地面上,动系 取在杆上,则 vel (1-r)@ de =(1-r)o- 重点要弄清楚牵 ye2=V7+r20 连点的概念 a2=V7+r2o2
例 如图杆长l,绕O轴以角速 度 转动,圆盘半径为r,绕 轴以角速度 转动。求圆盘边 缘 和 点的牵连速度和加速 度。 o M1 M2 解:静系取在地面上,动系 取在杆上,则 ve1 = (l − r) 2 1 ae = (l − r) 2 2 2 v l r e = + 2 2 2 ae2 = l + r o o M1 M2 e1 v e1 a e2 v e2 a 重点要弄清楚牵 连点的概念
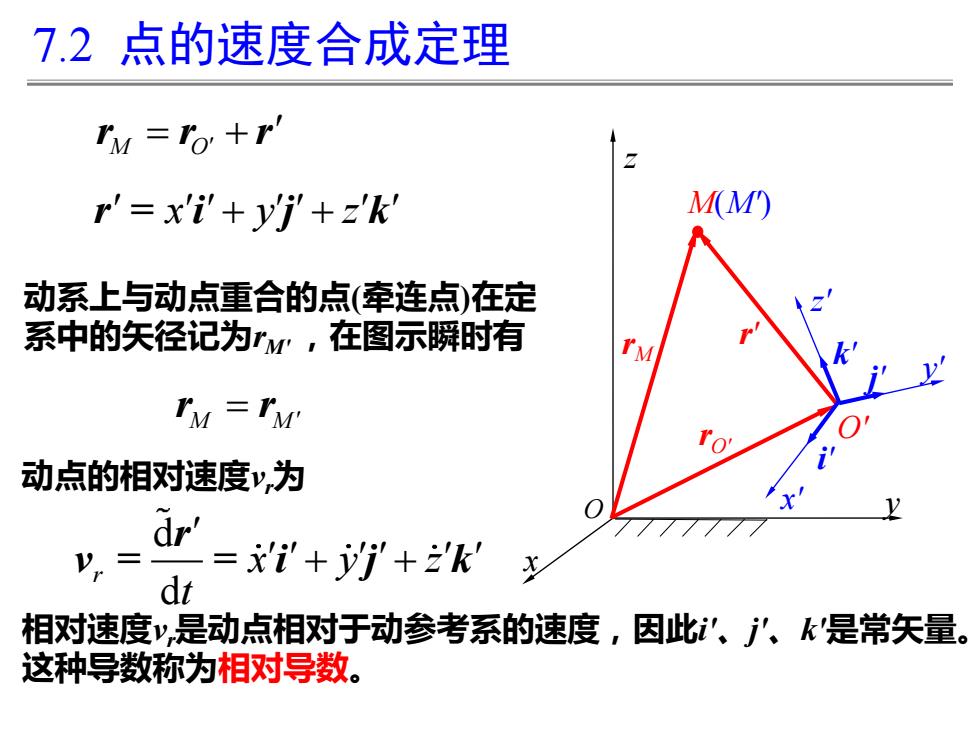
7.2点的速度合成定理 ry =To +r' r'=x'i'+yi+z'k M(M) 动系上与动点重合的点(牵连点)在定 系中的矢径记为rM,在图示瞬时有 ry =rM 动点的相对速度y,为 dr' y,= ='++k dt 相对速度v,是动点相对于动参考系的速度,因此”、'、k是常矢量。 这种导数称为相对导数
7.2 点的速度合成定理 rM rO' r' M(M') O' j' k' i' y' z' x' x y z O M O r r r = + r = i j k x y z + + M M = r r d d r x y z t + + r v = = i j k 动系上与动点重合的点(牵连点)在定 系中的矢径记为rM' ,在图示瞬时有 相对速度vr是动点相对于动参考系的速度,因此i'、j'、k'是常矢量。 这种导数称为相对导数。 动点的相对速度vr为

7.2点的速度合成定理 动点的牵连速度y为 drr=to+xi+yk M(M) dt 牵连速度是牵连点M'点的速 度,该点是动系上的点,因 此它在动系上的坐标'、y'、 z是常量。 动点的绝对速度为 4=。+x7+y+zW年置+训+k dt =Ve+v
7.2 点的速度合成定理 rM rO' r' M(M') O' j' k' i' y' z' x' x y z O d d M e O x y z t + + + r v = = r i j k d d M a O e r x y z x y z t + + + + + + r v = = r i j k + i j k = v v 动点的牵连速度ve为 牵连速度是牵连点M'点的速 度,该点是动系上的点,因 此它在动系上的坐标x'、y'、 z'是常量。 动点的绝对速度va为

7.2点的速度合成定理 Va =Ve +Vr 即:动点在某一瞬时的绝对速 度等于它在该瞬时的牵连速度 与相对速度的矢量和。这就是 点的速度合成定理
v v v a e r = + 即:动点在某一瞬时的绝对速 度等于它在该瞬时的牵连速度 与相对速度的矢量和。这就是 点的速度合成定理。 7.2 点的速度合成定理

7.2点的速度合成定理 处理具体问题时应注意: ()选取动点、动参考系和定参考系。 动点和动系应分别选择在两个不同的刚体上。 动点和动系的选择应使相对运动的轨迹简单直观。 在有的机构中,一个构件上总有一个点被另一个构件 所束。这时,以被约束的点作为动点,在约束动点 的构件上建立动系,相对运动轨迹便是约束构件的轮 廓线或者约束动点的轨道。 (2)应用速度合成定理时,可利用速度平行四边形中的 几何关系解出未知数。也可以采用投影法:即等式左 右两边同时对某一轴进行投影,投影的结果相等
处理具体问题时应注意: (1) 选取动点、动参考系和定参考系。 (2) 应用速度合成定理时,可利用速度平行四边形中的 几何关系解出未知数。也可以采用投影法:即等式左 右两边同时对某一轴进行投影,投影的结果相等。 动点和动系应分别选择在两个不同的刚体上。 动点和动系的选择应使相对运动的轨迹简单直观。 7.2 点的速度合成定理 在有的机构中,一个构件上总有一个点被另一个构件 所约束。这时,以被约束的点作为动点,在约束动点 的构件上建立动系,相对运动轨迹便是约束构件的轮 廓线或者约束动点的轨道