
第二章随机变量及其分布 2.4条件分布和随机变量的独立性 2.4.1条件分布 1 2.4.2随机变量的独立性.. 10 Previous Next First Last Back Forward 1
第二章随机变量及其分布 2.4 条件分布和随机变量的独立性 . . . . . . . . . 1 2.4.1 条件分布 . . . . . . . . . . . . . . . . 1 2.4.2 随机变量的独立性 . . . . . . . . . . . 10 Previous Next First Last Back Forward 1

2.4条件分布和随机变量的独立性 2.4.1条件分布 一个随机变量(或向量)的条件概率分布,就是在给定(或已知) 某种条件(某种信息)下该随机变量(向量)的概率分布。 1.离散型随机变量的条件分布 设(X,Y)为二维离散型随机变量,其全部的可能取值为{(x,): i,方=1,2,…}。记其联合分布律为 Pij P(X=i,Y=yj), i,j=1,2, 若对给定的事件{Y=},其概率P(Y=)>0,则称 P(X=Y=)=PX=y二=,i=1,2 P(Y=) p-i Previous Next First Last Back Forward
2.4 条件分布和随机变量的独立性 2.4.1 条件分布 一个随机变量 (或向量) 的条件概率分布,就是在给定 (或已知) 某种条件 (某种信息) 下该随机变量 (向量) 的概率分布。 1. 离散型随机变量的条件分布 设 (X, Y ) 为二维离散型随机变量,其全部的可能取值为 {(xi, yj ) : i, j = 1, 2, · · · }。记其联合分布律为 pij = P(X = xi, Y = yj ), i, j = 1, 2, · · · 若对给定的事件 {Y = yj},其概率 P(Y = yj ) > 0,则称 P(X = xi|Y = yj ) = P(X = xi, Y = yj ) P(Y = yj ) = pij p·j , i = 1, 2, · · · Previous Next First Last Back Forward 1

为在给定Y=的条件下X的条件分布律(概率函数)。类似的, 若P(X=x)>0,则称 PY=K==PX2=兴,j=12, P(X=Ii) Pi. 为在给定条件X=x:下Y的条件分布律。 Previous Next First Last Back Forward 2
为在给定 Y = yj 的条件下 X 的条件分布律 (概率函数)。类似的, 若 P(X = xi) > 0,则称 P(Y = yj |X = xi) = P(X = xi, Y = yj ) P(X = xi) = pij pi· , j = 1, 2, · · · 为在给定条件 X = xi 下 Y 的条件分布律。 Previous Next First Last Back Forward 2
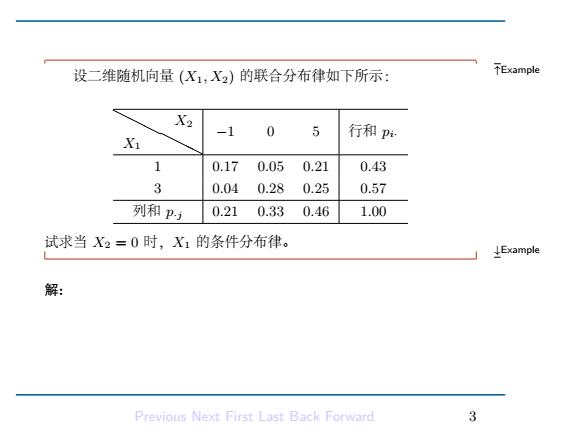
设二维随机向量(X1,X2)的联合分布律如下所示: TExample X2 -1 0 5 行和p X1 1 0.17 0.05 0.21 0.43 3 0.04 0.28 0.25 0.57 列和p 0.21 0.33 0.46 1.00 试求当X2=0时,X1的条件分布律。 ↓Example 解: Previous Next First Last Back Forward %
↑Example 设二维随机向量 (X1, X2) 的联合分布律如下所示: ❍ X ❍ 1 ❍❍❍❍ X2 −1 0 5 行和 pi· 1 0.17 0.05 0.21 0.43 3 0.04 0.28 0.25 0.57 列和 p·j 0.21 0.33 0.46 1.00 试求当 X2 = 0 时,X1 的条件分布律。 ↓Example 解: 由联合分布律先算出两个边缘分布律 pi· 与 p·j 并填入表中,由 此进一步算出条件分布律为: P{X1 = 1|X2 = 0} = 0.05 0.33 = 5 33 而 P{X1 = 3|X2 = 0} = 0.28 0.33 = 28 33 . Previous Next First Last Back Forward 3

设X=(X1,X2,…,Xn)~M(N;p1,p2,…,pn),试求X在 TExample 给定X2=k的条件下的条件分布律。 ↓Example 解: Previous Next First Last Back Forward 4
↑Example 设 X = (X1, X2, · · · , Xn) ∼ M(N; p1, p2, . . . , pn),试求 X1 在 给定 X2 = k 的条件下的条件分布律。 ↓Example 解: 由于易知 (X1, X2) ∼ M(N; p1, p2, 1 − p1 − p2),即其联合分 布律为 P(X1 = i, X2 = j) = N! i!j!(N − i − j)! p i 1p j 2 (1 − p1 − p2) N−i−j 其中 0 ≤ i, j ≤ N & 0 ≤ i + j ≤ N 并且 X2 ∼ B(N, p2). 因此 P(X1 = i|X2 = k) = P(X1 = i, X2 = k) P(X2 = k) = N! i!k!(N − i − k)! p i 1p k 2 (1 − p1 − p2) N−i−k / C k N p k 2 (1 − p2) N−k = (N − k)! i!(N − k − i)! ( p1 1 − p2 )i ( 1 − p1 1 − p2 )N−k−i , i = 0, 1, · · · , N − k. Previous Next First Last Back Forward 4