
第五章:数理统计的基本概念与抽样分布 4.1 三大分布 1 4.1.1X2分布 1 4.1.2t分布 7 4.1.3 F分布 12 4.1.4 正态总体样本均值和样本方差的分布· 16 4.1.5 几个重要推论... 18 4.2总结.·. 23 Previous Next First Last Back Forward 1
第五章: 数理统计的基本概念与抽样分布 4.1 三大分布 . . . . . . . . . . . . . . . . . . . . 1 4.1.1 χ 2 分布 . . . . . . . . . . . . . . . . . 1 4.1.2 t 分布 . . . . . . . . . . . . . . . . . . 7 4.1.3 F 分布 . . . . . . . . . . . . . . . . . 12 4.1.4 正态总体样本均值和样本方差的分布 . 16 4.1.5 几个重要推论 . . . . . . . . . . . . . . 18 4.2 总结 . . . . . . . . . . . . . . . . . . . . . . . 23 Previous Next First Last Back Forward 1

4.1三大分布 能求出抽样分布的确切而且具有简单表达式的情形并不多,一般 都较难.所幸的是,在总体分布为正态情形,许多重要统计量的抽样分 布可以求得,这些多与下面讨论的三种分布有密切关系.这三个分布 在后面几章中有重要应用. 4.1.1 X2分布 设X,X2,…,Xmi.1.d.心N(0,1),令X=∑X经,则称 X是自由度为n的X2交量,其分布称为自由度为n的X2 Definition 分布,记为X心X后 Previous Next First Last Back Forward
4.1 三大分布 能求出抽样分布的确切而且具有简单表达式的情形并不多, 一般 都较难. 所幸的是, 在总体分布为正态情形, 许多重要统计量的抽样分 布可以求得, 这些多与下面讨论的三种分布有密切关系. 这三个分布 在后面几章中有重要应用. 4.1.1 χ 2 分布 设 X1, X2, · · · , Xn i.i.d. ∼ N(0, 1), 令 X = ∑n i=1 X 2 i , 则称 X 是自由度为 n 的 χ 2 变量, 其分布称为自由度为 n 的χ 2 分布, 记为 X ∼ χ 2 n. Definition Previous Next First Last Back Forward 1

设随机变量X是自由度为n的X2随机变量,则其概率密度函 数为 Im-e-,x>0. 2登r(号) (4.1) 0. x≤0. X的密度函数g(x)形状如下图 Previous Next First Last Back Forward 2
设随机变量 X 是自由度为 n 的 χ 2 随机变量, 则其概率密度函 数为 gn(x) = 1 2 n 2 Γ( n 2 ) x n 2 −1 e − x 2 , x > 0, 0, x ≤ 0. (4.1) χ 2 n 的密度函数 gn(x) 形状如下图 Previous Next First Last Back Forward 2
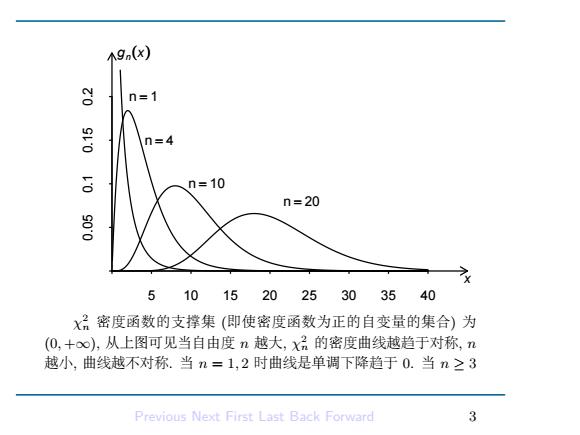
9n(x) n=1 n=4 n=10 n=20 510152025303540 X?密度函数的支撑集(即使密度函数为正的自变量的集合)为 (0,+o∞),从上图可见当自由度n越大,X的密度曲线越趋于对称,n 越小,曲线越不对称.当n=1,2时曲线是单调下降趋于0.当n≥3 Previous Next First Last Back Forward 3
5 10 15 20 25 30 35 40 0.05 0.1 0.15 0.2 gn(x) x n = 1 n = 4 n = 10 n = 20 χ 2 n 密度函数的支撑集 (即使密度函数为正的自变量的集合) 为 (0, +∞), 从上图可见当自由度 n 越大, χ 2 n 的密度曲线越趋于对称, n 越小, 曲线越不对称. 当 n = 1, 2 时曲线是单调下降趋于 0. 当 n ≥ 3 Previous Next First Last Back Forward 3

时曲线有单峰,从0开始先单调上升,在一定位置达到峰值,然后单下 降趋向于0. 若X~X品,记P(X>c)=a,则c=X(a)称为X品分布的上 侧a分位数,如下图所示.当a和n给定时可查表求出X品(a)之值, 如X1(0.01)=23.209,x(0.05)=12.592等. 个9n(x) x(a) Previous Next First Last Back Forward 4
时曲线有单峰, 从 0 开始先单调上升, 在一定位置达到峰值, 然后单下 降趋向于 0. 若 X ∼ χ 2 n, 记 P(X > c) = α, 则 c = χ 2 n(α) 称为 χ 2 n 分布的上 侧 α 分位数, 如下图所示. 当 α 和 n 给定时可查表求出 χ 2 n(α) 之值, 如 χ 2 10(0.01) = 23.209, χ2 5(0.05) = 12.592 等. α χn 2 (α) x gn(x) Previous Next First Last Back Forward 4