
第一章事件与概率 1.5条件概率 2 1.5.1全概率公式和Bayes公式 10 1.5.2事件的独立性 20 Previous Next First Last Back Forward 1
第一章事件与概率 1.5 条件概率 . . . . . . . . . . . . . . . . . . . . 2 1.5.1 全概率公式和 Bayes 公式 . . . . . . . 10 1.5.2 事件的独立性 . . . . . . . . . . . . . . 20 Previous Next First Last Back Forward 1

1.5条件概率 1.条件概率的定义 一般讲,条件概率就是在知道了一定的信息下所得到的随机事件 的概率.如两个工厂A和B生产同一品牌的电视机,商场中该品牌 有个统一的次品率,比如0.5%,如果你从某个途径知道该商场的这批 电视机是A厂生产的,则你买到的电视机的次品率不再是0.5%,这 个概率就是条件概率 设事件A和B是随机试验2中的两个事件,P(B)>0, 称 P(AB)= P(AB) Definition P(B) 为事件B发生条件下事件A发生的条件概率. Previous Next First Last Back Forward 2
1.5 条件概率 1. 条件概率的定义 一般讲, 条件概率就是在知道了一定的信息下所得到的随机事件 的概率. 如两个工厂 A 和 B 生产同一品牌的电视机, 商场中该品牌 有个统一的次品率, 比如 0.5%, 如果你从某个途径知道该商场的这批 电视机是 A 厂生产的, 则你买到的电视机的次品率不再是 0.5%, 这 个概率就是条件概率. 设事件 A 和 B 是随机试验 Ω 中的两个事件, P(B) > 0 , 称 P(A|B) = P(AB) P(B) 为事件 B 发生条件下事件 A 发生的条件概率. Definition Previous Next First Last Back Forward 2
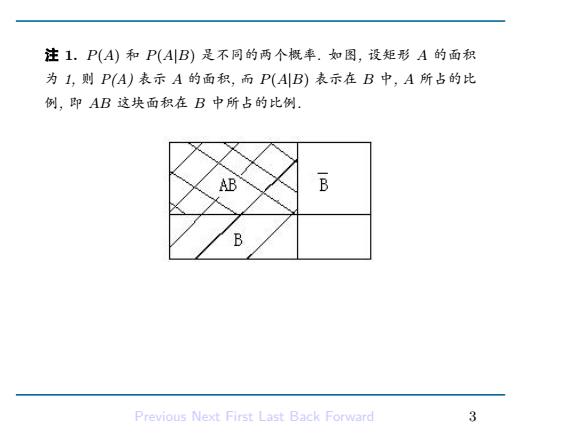
注1.P(A)和P(AB)是不同的两个概率.如图,设矩形A的面积 为1,则P(A)表示A的面积,而P(AB)表示在B中,A所占的比 例,即AB这块面积在B中所占的比例. AB B B Previous Next First Last Back Forward 2
注 1. P(A) 和 P(A|B) 是不同的两个概率. 如图, 设矩形 A 的面积 为 1, 则 P(A) 表示 A 的面积, 而 P(A|B) 表示在 B 中, A 所占的比 例, 即 AB 这块面积在 B 中所占的比例. Previous Next First Last Back Forward 3

注2.可以从概率的统计定义,即用频率来近似概率这一角度来理解 条件概率.设在n次独立试验中,事件A发生了nA次,事件B发 生了nB次,事件AB发生了nAB次,事件B发生下事件A发生 的频率为 AE≈PAB n P(B) 注3.事实上,我们所考虑的概率都是在一定条件下计算的,因为随 机试验就是在一定的条件下进行的,所以样本空间是相对而言的.如 果把在一定条件下的随机试脸看成无条件的,则在补充条件下进行的 随机试验的结果一般而言相对于原有结果要少,即样本空间改变了 所以所得随机事件的概率一般是不相同的. Previous Next First Last Back Forward 4
注 2. 可以从概率的统计定义, 即用频率来近似概率这一角度来理解 条件概率. 设在 n 次独立试验中, 事件 A 发生了 nA 次, 事件 B 发 生了 nB 次, 事件 AB 发生了 nAB 次, 事件 B 发生下事件 A 发生 的频率为 nAB nB ≈ P(AB) P(B) 注 3. 事实上, 我们所考虑的概率都是在一定条件下计算的, 因为随 机试验就是在一定的条件下进行的, 所以样本空间是相对而言的. 如 果把在一定条件下的随机试验看成无条件的, 则在补充条件下进行的 随机试验的结果一般而言相对于原有结果要少, 即样本空间改变了. 所以所得随机事件的概率一般是不相同的. Previous Next First Last Back Forward 4

TExample 有10个产品,内有3个次品,从中一个个地抽取(不放回)检验 问第一次取到次品后第二次再取到次品的概率 ↓Example 解 Previous Next First Last Back Forward 5
↑Example 有 10 个产品, 内有 3 个次品, 从中一个个地抽取 (不放回) 检验, 问第一次取到次品后第二次再取到次品的概率. ↓Example 解: 样本空间 Ω 是从 10 个产品中有序取出 2 个产品的不同方法, 这 是一个排列问题, 易知 |Ω| = 10 × 9 = 90, 记 A ={第一次取出的是次 品}, B ={第二次取出的是次品}, |AB| = 6, |A| = 3, 故 P(B|A) = P(AB) P(A) = 6/90 3/10 = 2/9 注意, P(B|A) = 2/9 ̸= P(A) = 3/10. Previous Next First Last Back Forward 5