
第四节二项资料的百分数假设检验 Test of percent hypothesis ·适用于以百分数或成数表示试验的结果分析。 如病株率、有虫株率、杀虫率、发芽率等。 ·理论上讲,这类资料应按照二项分布进行,但当样本 容量n较大,p不过小,np、ng又均不小于5时, (p+q的分布趋近于正态分布,因而,可将百分数的 资料作正态分布处理
• 适用于以百分数或成数表示试验的结果分析。 如病株率、有虫株率、杀虫率、发芽率等。 • 理论上讲,这类资料应按照二项分布进行,但当样本 容量n较大,p不过小,np、nq又均不小于5时, (p+q) n的分布趋近于正态分布,因而,可将百分数的 资料作正态分布处理。 第四节 二项资料的百分数假设检验 Test of percent hypothesis
第四节二项资料的百分数假设检验 Test of percent hypothesis 二项资料在以下情况可以用U测验进行分析。 适合于用正态离差测验的二项样本的np和n值表 样本百分数D 较小组次数np 样本容量n 0.50 15 30 0.40 20 50 0.30 24 80 0.20 40 200 0.10 60 600 0.05 70 1400 注意表中p、np以及n的关系
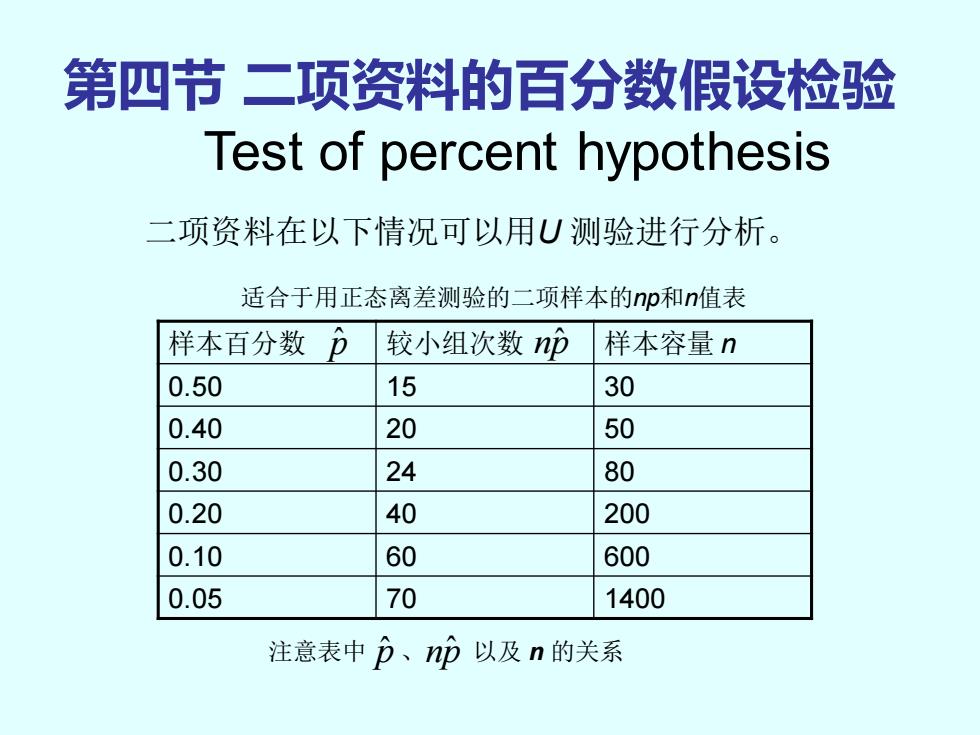
第四节 二项资料的百分数假设检验 Test of percent hypothesis 二项资料在以下情况可以用U 测验进行分析。 适合于用正态离差测验的二项样本的np和n值表 样本百分数 较小组次数 样本容量 n 0.50 15 30 0.40 20 50 0.30 24 80 0.20 40 200 0.10 60 600 0.05 70 1400 p ˆ np ˆ 注意表中 p ˆ 、np ˆ 以及 n 的关系

第四节二项资料的百分数假设检验 Test of percent hypothesis 1、单个样本百分数的假设测验 2、两个样本百分数相比较的假设测验 3、二项样本假设测验时的连续矫正
第四节 二项资料的百分数假设检验 Test of percent hypothesis 1、单个样本百分数的假设测验 2、两个样本百分数相比较的假设测验 3、二项样本假设测验时的连续矫正

Test of percent hypothesis 二项总体抽样的分布 二项总体的平均数则=p,方差σ2=p(1-p)=pq 标准差为o=Vp(I-p)=Vpg 样本平均数抽样分布 平均数,4=卫 方差, :=pq n 标准误, 0: =pa-p)
二项总体抽样的分布 二项总体的平均数μ=p,方差σ2 =p(1-p)=p q 标准差为 = p(1− p) = pq 样本平均数抽样分布 平均数, 方差, 标准误, n p p n pq n pq p x x x (1 ) 2 − = = = = Test of percent hypothesis

二项总体的分布参数 ·例:一个总体内有5个个体,分别为0、1、0、1、1。 ·则:W=(0+1+0+1+1)÷5=0.6 ·所以u=p ·σ2=[0-0.6)2+(1-0.6)2++(0-0.6)2]÷5=0.24 区②5-a o=√0.24=0.49 (每次取一个样,即:n=1)
二项总体的分布参数 • 例:一个总体内有5个个体,分别为0、1、0、1、1。 • 则:μ=( 0+1 + 0 + 1 + 1 )÷5=0.6 • 所以μ= p • σ2=[(0-0.6)2+(1-0.6)2+.+(0-0.6)2 ]÷5=0.24 = 0.24 = 0.49 ( ) 5 0.24 5 9 3 2 2 2 = = − = − n n x x (每次取一个样,即: n =1)