
第二章随机变量 离散型随机变量 随机变量的分布函数 连续型随机变量 一维随机变量函数的分布 号二维随机变量的联合分布 多维随机变量的边缘分布与独立性 号条件分布 “多维随机变量函数的分布
第二章随机变量 离散型随机变量 随机变量的分布函数 连续型随机变量 一维随机变量函数的分布 二维随机变量的联合分布 多维随机变量的边缘分布与独立性 条件分布 多维随机变量函数的分布

关于随机变量及向量的研究,是概率论的 中心内容.这是因为,对于一个随机试验,我 们所关心的往往是与所研究的特定问题有关的 某个或某些量,而这些量就是随机变量。也可 以说:随机事件是从静态的观点来研究随机现 象,而随机变量则是一种动态的观点,一如数 学分析中的常量与变量的区分那样.变量概念 是高等数学有别于初等数学的基础概念.同样, 概率论能从计算一些孤立事件的概念发展为一 个更高的理论体系,其基础概念是 随机变量
关于随机变量(及向量)的研究,是概率论的 中心内容.这是因为,对于一个随机试验,我 们所关心的往往是与所研究的特定问题有关的 某个或某些量,而这些量就是随机变量.也可 以说:随机事件是从静态的观点来研究随机现 象,而随机变量则是一种动态的观点,一如数 学分析中的常量与变量的区分那样.变量概念 是高等数学有别于初等数学的基础概念.同样, 概率论能从计算一些孤立事件的概念发展为一 个更高的理论体系,其基础概念是 随机变量

2.1随机变量的概念 (p24)定义.设S={e}是试验的样本空 间,如果量X是定义在$上的一个单 A(e 值实值函数即对于每一个e∈S,有一 实数X=X(e)与之对应,则称X为随机 变量。 随机变量常用X、Y、Z或、 等表示。 随机变量的特点: 1X的全部可能取值是互斥且完备的 2X的部分可能取值描述随机事件
2.1随机变量的概念 (p24)定义. 设S={e}是试验的样本空 间,如果量X是定义在S上的一个单 值实值函数即对于每一个eS,有一 实数X=X(e)与之对应,则称X为随机 变量。 随机变量常用X、Y、Z 或 、、 等表示。 随机变量的特点: 1 X的全部可能取值是互斥且完备的 2 X的部分可能取值描述随机事件

7 请举几个实际中随机变量的例子 EX.引入适当的随机变量描述下列事件: ①将3个球随机地放入三个格子中, 事件A={有1个空格},B={有2个空格}, C={全有球}。 ②进行5次试验,事件D={试验成功一次}, F={试验至少成功一次},G={至多成功3次}
EX.引入适当的随机变量描述下列事件: ①将3个球随机地放入三个格子中, 事件A={有1个空格},B={有2个空格}, C={全有球}。 ②进行5次试验,事件D={试验成功一次}, F={试验至少成功一次},G={至多成功3次}
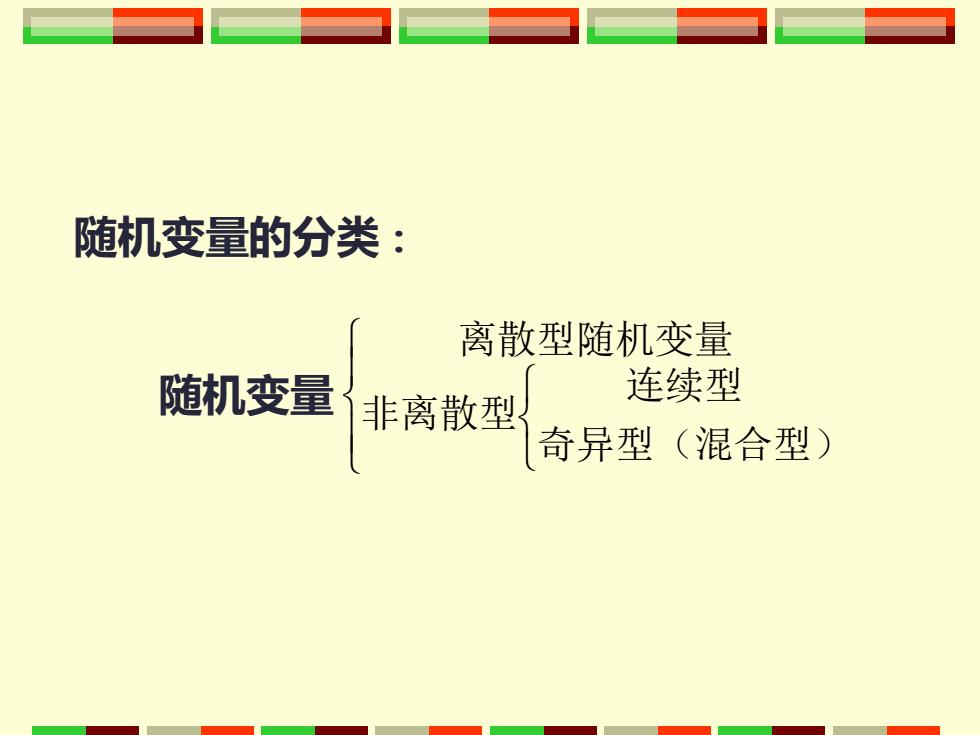
随机变量的分类: 离散型随机变量 随机变量 连续型 非离散型 奇异型(混合型)
奇异型(混合型) 连续型 非离散型 离散型随机变量 随机变量的分类: 随机变量