
Test of percent hypothesis 1、单个样本百分数的假设测验 。 测试百分数B所属总体百分数与某一理论值或期望值P的 差异显著性。 。样本百分数的标准误为: 0=1 故由 u= -Po 例:紫花与白花大豆杂交,在F2代共得到289株,其中紫 花208株,白花81株。如果花色受一对等位基因控制,根 据遗传学原理,F2代紫花与白花分离的比例应为3:1,即 紫花理论数为p=0.75,白花为q=1-p=0.25。问该试验是 否符合一对等位基因的的遗传规律?
1、单个样本百分数的假设测验 • 测试百分数β所属总体百分数与某一理论值或期望值p0的 差异显著性。 • 样本百分数的标准误为: n p (1 p ) 0 0 ˆ − = 故由 p p p u ˆ 0 ˆ − = 例:紫花与白花大豆杂交,在F2代共得到289株,其中紫 花208株,白花81株。如果花色受一对等位基因控制,根 据遗传学原理,F2代紫花与白花分离的比例应为3:1,即 紫花理论数为p=0.75,白花为q =1-p =0.25。问该试验是 否符合一对等位基因的的遗传规律? Test of percent hypothesis

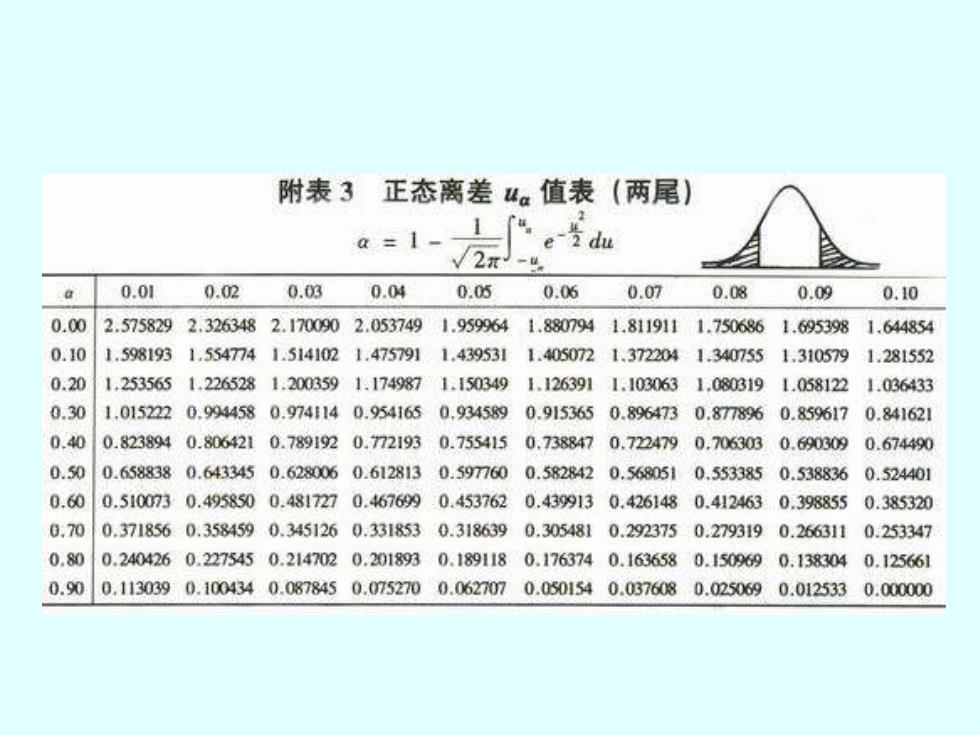
单个样本百分数的假设测验 ·假设:Ho:p=0.75;Ha:p0.75.0=0.05, 作两尾测验uo5=1.96。 计算: 208 p= =0.7197 0.75×0.25 =0.0255 289 Op= 289 4 0.7197-0.75 =-1.19 0.0255 因为:u05=1.96,|u|(1.19)<u0.05,所以p>0.05。 推断:接受Ho:p=0.75,即该试验中大豆花色符合一对等位 基因的遗传规律。试验中的p=0.7197与p=0.75的差别属于随 机误差
• 假设:H0:p=0.75;HA:p≠0.75。α=0.05, 作两尾测验u.05=1.96。 0.7197 289 208 p ˆ = = 计算: 0.0255 289 0.75 0.25 ˆ = p = 1.19 0.0255 0.7197 0.75 = − − u = 因为:u.05=1.96,│u│(1.19)<u0.05,所以p>0.05。 推断:接受H0:p=0.75,即该试验中大豆花色符合一对等位 基因的遗传规律。试验中的p=0.7197与p=0.75的差别属于随 机误差。 单个样本百分数的假设测验
附表3正态离差4。值表(两尾) a= 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.00 2.5758292.3263482.1700902.0537491.9599641.8807941.8119111.7506861.695381.644854 0.10 1.5981931.5547741.5141021.4757911.439531 1.4050721.3722041.3407551.3105791.281552 0.20 1.2535661.2265281.2003591.1749871.1503491.1263911.1030631.0803191.058122 1.036433 0.30 1.0152220.9944580.9741140.9541650.9345890.9153650.8964730.8778960.859617 0.841621 0.40 0.8238940.8064210.7891920.7721930.7554150.7388470.722479 0.7063030.690309 0.674490 0.50 0.6588380.6433450.6280060.6128130.5977600.5828420.568051 0.5533850.538836 0.524401 0.60 0.5100730.4958500.4817270.4676990.4537620.4399130,4261480.4124630.398855 0.385320 0.70 0.3718560.3584590.3451260.3318530.3186390.3054810.2923750.2793190.266311 0.253347 0.80 0.2404260.2275450.2147020.2018930.1891180.1763740.1636580.150969 0.1383040.12566】 0.90 0.1130390.1004340.0878450.0752700.06270m0.0501540.0376080.0250690.0125330.000000

Test of percent hypothesis 2、两个样本百分数相比较的假设测验 。 测验两个样本百分数p和p,所属总体百分数p1和p2的差异 显著性。 一 般假设两个样本总体方差是相等的,即o=o 两个样本总体的个体百分数不同为p1和p2。两个样本百分 数的差数标准误为: -p2 P19+P292 n n 如果两总体的百分数相同,即p1=p2=p,91=q2=q,则:
2、两个样本百分数相比较的假设测验 • 测验两个样本百分数 和 所属总体百分数p1和p2的差异 显著性。 • 一般假设两个样本总体方差是相等的,即 • 两个样本总体的个体百分数不同为p1和p2。两个样本百分 数的差数标准误为: 2 ˆ 2 ˆp1 p2 = 1 p ˆ 2 p ˆ 2 2 2 1 1 1 ˆ ˆ 1 2 n p q n p q p − p = + 如果两总体的百分数相同,即p1=p2=p,q1=q2=q,则: − = + 1 2 ˆ ˆ 1 1 1 2 n n p p pq Test of percent hypothesis

Test of percent hypothesis 2、两个样本百分数相比较的假设测]验 在两个总体百分数p1和p2未知时,在两个总体方 差相等的前提下(σ=o员),可用两样本百分 数的加权平均值作为p1和p2的估计。即: p=龙+为 n1+n2 两个样本百分数的差数标准误为: 故有: 4=p-2 0n-p2 即可对Ho:p=p2作出假设测验
2、两个样本百分数相比较的假设测验 • 在两个总体百分数p1和p2未知时,在两个总体方 差相等的前提下( ),可用两样本百分 数的加权平均值作为p1和p2的估计。即: − = + 1 2 ˆ ˆ 1 1 1 2 n n p p pq 故有: 2 ˆ 2 ˆp1 p2 = 1 2 1 2 n n x x p + + = 两个样本百分数的差数标准误为: 1 2 ˆ ˆ 1 2 ˆ ˆ p p p p u − − = 即可对H0:p1=p2作出假设测验。 Test of percent hypothesis